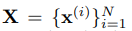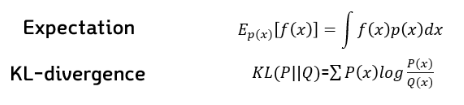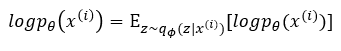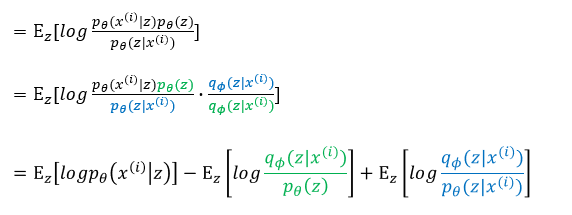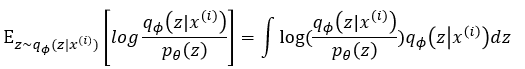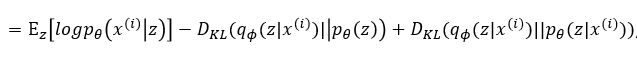VAE : Auto-Encoding Variational Bayes

오늘은 대망의 VAE를 리뷰해보겠습니다!
이번 논문은 수식이 많아 까다롭게 느껴질 수 있지만, 천천히 논리들을 따라가며 리뷰를 진행해보겠습니다. 논문을 볼 때 마다 읽다보면 오 그렇구나 하며 읽지만, 사실 이것을 애초에 어떻게 생각해냈을까 생각해보면 정말 대단한 것 같습니다.
논문마다 다르지만 성능을 높이고자 하는 논문은 주로 완벽한 증명을 요하는 것이 아니기에 유도리가 필요한 부분도 존재하는 것 같습니다.
(하지만 재미는 점은 이 유도리있게 진행한 이유에 대한 근거는 필요합니다!)
본 논문에서도 확률분포를 근사시키고, 알 수 없는 부분에 대해서는 maximum의 minimum을 설정하여 논리를 진행시키는 등 많은 trick들을 사용합니다.

0. Abstract

본 논문은 "다루기 어려운 intractable한 사후(posterior) 확률분포를 가진 연속적인 latent varialbes(잠재 변수)와 대규모 데이터셋이 있는 경우, 어떻게 하면 방향성 확률 모델에서 효율적인 추론과 학습을 진행할 수 있을까?" 라는 질문에서 시작합니다.
이에 대하여 큰 데이터셋에서도 확장할 수 있고 mild(가벼운)한 미분가능성이 조건이 있다면 계산이 불가능한 경우에도 작동하는 stochastic variational inference and learning 알고리즘을 제안합니다.
본 논문의 기여는 두 가지 입니다.

첫번 째) variational lower bound의 reparameterization이 표준적인 stochastic gradient 방법론들을 사용하여 직접적으로 최적화될 수 있는 lower bound estimator를 만들어낸다는 것을 보였습니다.

두번 째) 각 datapoint가 연속형 잠재 변수를 가지는 i.i.d. 데이터셋에 대해서, 위에서 제안된 lower bound estimator를 사용해 approximate inference model(또는 recognition model)을 계산이 불가능한 posterior에 fitting 시킴으로써 posterior inference가 특히 효율적으로 만들어질 수 있다는 점을 보입니다.

VAE 이해하기 위한 내용(1) - Gradient Descent Optimization Algorithms
VAE 이해하기 위한 내용(2) - iid / 확률분포
VAE 이해하기 위한 내용(3) - Posterior과 Bayesian

1. Introduction

Q. 연속적인 잠재 변수 혹은 파라미터에서 풀 수 없는 사후 분포(intractable posterior distribution)를 가지는 directed probabilistic model을 효율적으로 근사치에 추정하고 학습할 수 있을까?

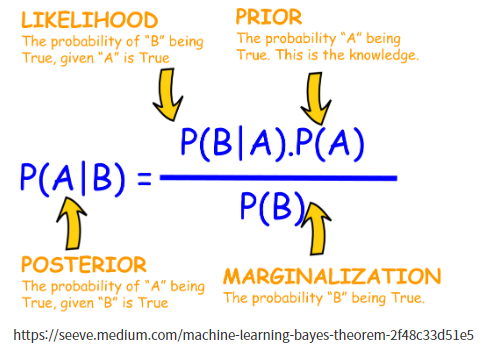
VB(Variational Bayesian) 접근 방식은 다루기 힘든 사후 확률(posterior)에 대한 근사의 최적화를 포함합니다. : 베이지안 추론을 근사화하는 방법

variational lower bound의 reparameterization(재매개화)을 통해 단순하고 미분이 가능한 하한추정기인 Stochastic Gradient Variational Bayes(SGVB) 를 얻습니다. 이 SGVB를 통해 연속적인 잠재변수를 가진 모델에 대한 효율적인 근사 사후 추론을 진행하고, standard stochastic gradient를 통해 쉽게 최적화가 가능합니다.

iid dataset과 data point마다 연속적인 잠재 변수인 경우, AEVB(Auto-Encoding VB) 알고리즘을 사용할 수 있습니다. AEVB는 SGVB 추정기를 사용하여 효율적인 근사적 사후 추론과 모델 매개 변수의 효율적인 학습을 가능하게 하고, 학습된 근사 사후 추론 모델은 recognition, denoising, representation, visualization에 활용될 수 있습니다.

이에 더하여 신경망이 recognition model에 사용될 때, Variational Auto-Encoder: VAE가 됩니다!

intractable posterior distribution을 풀기 위해 어떻게 진행해야 하는지가 중심적인 내용입니다. 크게 두 가지로, 1) intractable posterior distribution을 위해서 진행하는 variational inference의 lower bound이며, 2) reparameterization을 통한 미분 가능성을 진행하는 것 입니다.
이를 위해 SGVB를 이용하여 효과적인 근사치 사후 추론이 가능하게 한 것 입니다.

2. Method

위의 Introduction에서 설명한 내용들을 기반으로 설명해보겠습니다.

연속적인 잠재 변수를 갖는 다양한 graphical model에 대한 lower bound estimator를 유도하는 전략에 대해 설명합니다. data point 마다 잠재변수가 있는 iid data set이라고 가정하고, 이 가정 하에서 전역 파라미터에 ML(maximum likelihood)나 MAP(maximum posterior)추론을 수행하고 잠재 변수에는 variational 추론을 하려고 합니다. 또한 단순성을 위해 static(fixed) 데이터 셋을 가정합니다.

2.1 Problem scenario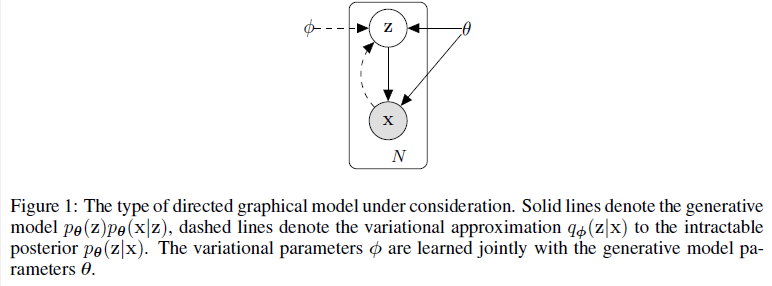

아래와 같은 N개의 iid 샘플로 구성된 데이터 셋을 고려합니다.

z : 관측되지 않은 연속 랜덤 변수 z
x : z를 포함하는 어떠한 랜덤 프로세스에 의해 생성

이 data set 각 x를 생성하는 과정은 크게 두 가지로 나뉩니다.
1) 잠재변수 z^(i)는 사전분포(prior distribution) pθ(z)로 부터 생성
2) data set x^(i)는 조건부확률(conditional distribution) pθ(x|z)로 부터 생성

이 때, prior과 likelihood는 parametic한 distribution pθ(z)와 pθ(x|z)로 나타낼 수 있다고 가정하고, 이 pdf들은 θ나 z에 대해 거의 모든 곳에서 미분 가능함을 가정하겠습니다.

하지만 실제 parameter θ* 의 값과 random variable(latent vector) z^(i)를 모르기에 모델링은 매우 어렵습니다.

여기서 중요한 점은, posterior을 구하기 위한 값 중 marginal probability p(x)를 쉽게 이용할 수 있다는 가정은 하지 않습니다. 다시 말해, 우리의 모델은 아래와 같은 경우에도 잘 작동하는 알고리즘에 관심이 있습니다.

• Intractability(margianl likelihood를 구할 수 없는 경우)
  1) marginal 우도의 적분 pθ(x) = ∫pθ(z)pθ(x|z)dz (왜냐하면 𝑝(𝑥,𝑧)=𝑝𝜃(𝑧)𝑝𝜃(𝑥|𝑧)이고, 모든 𝑧에 대해 𝑝(𝑥,𝑧)를 적분하면 𝑝(𝑥))
  2) 사후 밀도 pθ(z|x) = pθ(x|z)pθ(z)/pθ(x)
  3) mean-field VB 알고리즘
  위 세 가지 에 대한 적분에 대해 해결하기 어려운 경우
• large dataset
  monte carlo approximation을 염두한 구절 같습니다. 데이터가 너무 많아서 각 data point로 부터 sampling을 여러 번 해야 하기에 배치 최적화가 너무 비용이 많이 드는 경우.
  이는 작은 minibatch나 단일 데이터 포인트를 사용하여 매개 변수를 업데이트하고자 합니다.

본 논문에서는 위의 시나리오 하에서 관련한 세 가지 문제에 관심이 있고, 해결책을 제안합니다.

1) 파라미터 θ에 대한 효율적인 근사 ML, MAP 추정
이는 매개 변수 자체에 관심을 갖는 것이며, 이러한 파라미터를 사용하여 숨겨진 무작위 과정을 모방하고 실제 데이터와 유사한 가상 데이터를 생성할 수 있습니다.
2) 파라미터 θ의 선택에 따른 관측 값 x가 주어졌을 때, latent vector z의 효과적인 근사치 사후 추정(approximate posterior inference : pθ(x|z)).
데이터 표현화에 유용합니다.
3) 변수 x의 효율적인 approximation margianl infernece
x에 대한 사전 분포가 필요한 모든 추론 작업을 수행할 수 있습니다.(image denoising, inpainting and super-resolution)

위와 같은 문제들을 해결하기 위해 recognition model(probabilistic encoder) : qø(z|x) 를 도입합니다 (qø(z|x) : 추론하기 어려운 실제 사후 분포(true posterior) pθ(x|z)의 근사치)

• 정리
  • 인식 모델 매개변수 ø를 생성 모델의 매개변수 θ와 함께 학습
  • data point x가 주어지면 data point x가 생성될 수 있는 코드 z의 가능한 값들에 대한 분포(ex)가우시안)를 생성하는 확률적 인코더
  • pθ(x|z)는 z가 주어지면 해당하는 x의 가능한 값들에 대한 분포를 생성하는 확률적 디코더

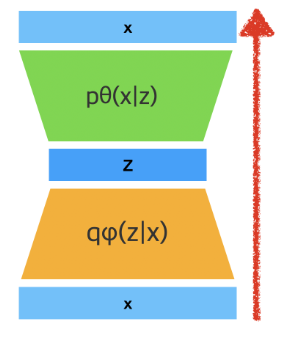
* 목표 : data likelihood 인 pθ(x) = ∫pθ(z)pθ(x|z)dz 를 최대화하는 것

pθ(x|z) : 디코더 neural network / pθ(z) : latent vecotr

But!
=> 위 식에서 모든 z에 대해 pθ(x|z)를 계산하는 것은 불가능

그렇다면 pθ(z|x) = pθ(x|z)pθ(z)/pθ(x) 은 어떨까?
=> 당연스럽게도 pθ(x)를 알 수 없기에 pθ(z|x)를 계산할 수 없다..

solution idea!
어떻게 하면 확률적 디코더 pθ(x|z)를 잘 만들어서, 실제 x값과 유사한 확률분포를 만들어낼 수 있을까?
네트워크의 출력값이 있을 때 우리가 원하는 정답 x가 나올 확률이 높길 바람
= x의 likelihood를 최대화하는 확률 분포를 찾자!
= Maximize Pθ(x) = ∫pθ(z)pθ(x|z)dz
: 확률적 디코더인 pθ(x|z)를 계산하는 것은 불가능하기에, encoder network인 qø(z|x)를 추가하여 pθ(x|z) 대신 근사화하자!

2.2 Variational Bound

우리가 원하는 것은 결국 x에 관한 marginal likelihood (logPθ(x)) 값입니다.

[ data likelihood : Pθ(x) = ∫pθ(z)pθ(x|z)dz ]
여기에 계산을 용이하게 함과 차후 쿨백-라이브러리 발산(두 확률분포의 차이를 계산하는데 사용하는 함수)을 이용하기 위해 로그를 씌우고, 우변은 기댓값으로 변환시켜줍니다.
여기서 확률분포를 자세히 살펴보시면 구하기 어려운 Pθ(x|z) 대신 recognition model qθ(z|x)로 대체된 것을 볼 수 있습니다.(그렇기에 기댓값은 z가 encoder를 거쳐서 나오는 확률 분포를 따를 때의 기댓값입니다) 또한 Pθ(z)도 Pθ(x)로 대체되었습니다.

이를 아래와 같이 베이즈 정리에 의해 식을 변경하고, KL발산을 이용하기 위해 식을 정리합니다.
이렇게 정리된 식은 다시 아래와 같은 방법으로 적분 형태로 바꿔준 후, KL발산을 통해 표현합니다.

이로써 식이 정리되었습니다!
하지만 이 식에서 또한 마지막 부분을 알 수 없습니다 : x가 주어졌을 때 z의 true값을 알 수 없기에 P(z|x)를 구할 수 없기 때문입니다.

하지만 이 식이 KLD이라는 것을 알고 이는 항상 0보다 크거나 같기에, 이 식의 전체에 대해 lower bound를 구합니다. 그리고 이 lower bound를 최대화 시켜줍니다!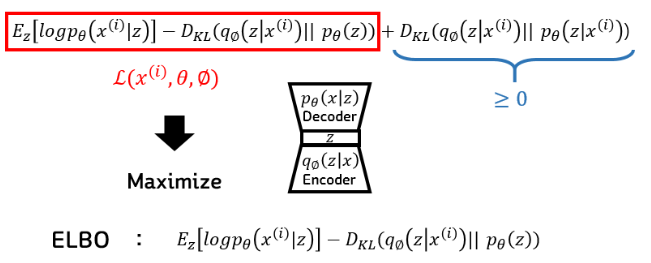
이는 베이즈 정리에서 Evidence에 해당되는 x에 대한 확률(marginal likelihood)을 구하는 것이기 때문에 Evidence LowerBOund 라고 해서 ELBO라고 불립니다.

이 ELBO를 이용하여 Loss ft을 구성하는데 아래와 같습니다. 보통 최적화에서는 minimize를 하기에 ELBO앞에 -를 붙이고, 이를 최소화시키는 파라미터 θ와 ϕ를 찾아주면 되는 것 입니다.

하지만!!
또 여기서 문제가 발생합니다. 우리는 이 lower bound를 variational parameter ϕ와 generative parameter θ에 대해 모두 최적화하고 싶은데, 이 lower bound로 gradient를 흘려보내 주는 것에 문제가 생깁니다. 일반적으로 monte carlo gradient estimator를 사용하는데 우리의 목적에는 실용적이지 않다고 합니다.

why?

• Monte carlo argorithm을 사용하지 않는 이유

무한한 경우의 수: 연속적인 잠재 변수에 대해서는 무한한 경우의 수가 있을 수 있습니다. 따라서 모든 가능한 값에 대해 기대값을 계산하려면 무한한 계산이 필요합니다. 실제로 이는 컴퓨터로 처리할 수 없는 불가능한 작업입니다.

정확한 적분 계산: 기대값은 해당 변수의 분포에 대한 적분으로 정의됩니다. 연속적인 잠재 변수의 분포를 수학적으로 정확하게 적분하는 것은 대부분의 경우 불가능합니다. 따라서 수치적인 적분 방법이나 샘플링 기법을 사용하여 근사적으로 계산해야 합니다.

그렇기에 Reconstruction error과 같이 기댓값 형식이기에 적분이 가능하지만 모든 z에 대해 적분이 어려운 경우, 보통은 몬테 카를로 추정을 사용하지만 딥러닝에서는 잘 쓰지 않는 이유입니다.

=> 따라서 VAE에서는 재매개변수화 트릭과 같은 방법을 사용하여 기댓값의 gradient를 효율적으로 추정합니다.

이 식은 두 term으로 구성됩니다.
1) Reconstruction error
어떤 input x가 들어왔을 때 -> 인코더 qϕ를 거쳐 z가되고 -> 이 z를 디코더 pθ(gθ)에 넣어 x가 나올 확률을 최대화 하는 term입니다.
2) Regularization
"x가 인코더 qϕ를 거쳐 나온 z : qϕ(z|x)"와 vs "우리가 가정한 z의 분포 : p(z)" 와 최대한 가깝게 만드는 term입니다.

계속해서 뒤에 나올 내용과 앞의 내용을 반복하다보니, 여기서부터는 논문의 목차와 관계없이 계속해서 진행되는 점 양해 부탁드립니다.

Regularization(제약 조건) 계산 : Encoder가 최소한의 학습 데이터는 잘 latent vector로 표현할 수 있게

regulization을 계산하기 위해서는 두 가지 가정이 필요합니다.
1) 인코더를 통과해서 나온 z 분포 qϕ(z|x)는 convariance가 diagonal한 multivariate 정규분포를 따릅니다.
2) 우리가 가정한 z의 분포인 prior p(z)는 평균이 0, 표준편차가 1인 표준정규분포를 따른다는 것 입니다.

즉, 인코더를 통과하면 multivariate 정규분포를 따르지만 z에 대한 분포는 평균이 0이고 표준편차가 1인 정규분포를 따른다고 가정한 것 입니다.
=> KLD를 사용하여 이 두 개의 가정을 같게 해주면서 최적화를 시킬 수 있습니다.
how?
우리가 multivariate 정규분포를 따른다고 했기에, KLD는 표준 정규분포에서 아래와 같이 표현되고,

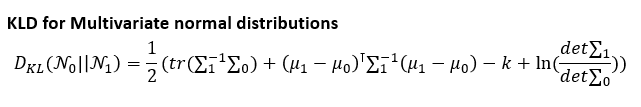
N1에 해당되는 p(z)를 평균이 0, 표준편차가 1인 정규분포를 가정했기에 뮤1=0, 시그마1=1로 값을 대입하여, 최종적으로 regulization term을 아래와 같이 표현할 수 있게됩니다.

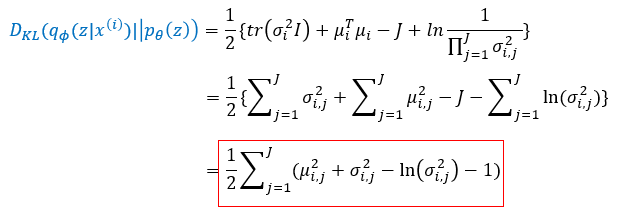
이렇게 변형한 식은 결국 뮤와 시그마만 남기 때문에 미분이 가능하고, 그렇기에 regulization을 계산할 수 있게 됩니다!

Reconstruction(복원 오차) 계산 : Decoder가 최소한의 학습 데이터는 생성해 낼 수 있게

Reconstruction error는 위에서 말한바와 같와 같습니다. 이 부분은 기댓값 형식으로 되어 있기에 적분이 가능합니다. 하지만 모든 z에 대해 적분은 어렵기에 몬테 카를로 추정을 사용하는데(무한개의 샘플링을 통한 평균) 시간이 너무 오래 걸리기에 여기서 L=1로 설정하여 이를 대표값으로 쓰게 됩니다. 즉, 랜덤하게 하나만 샘플링하여 그 값을 사용하는 것 입니다. 그렇게 변경한 식은 아래와 같습니다.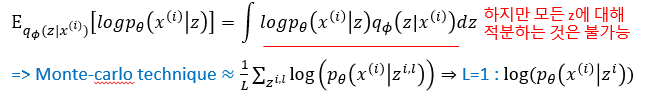

하지만 여기서의 식 또한 확률분포로 표현되어 있기 때문에 확률분포를 가정해야 계산이 가능합니다. 계산을 위해 두 가지 확률분포 가정을 통해 식을 변형합니다.

1) Bernoulli Distribution
베르누이 분포를 따른다고 가정했을 때, 독립시행이므로 각 차원별로 확률을 계산하기 때문에 곱하기로 표현이 가능하고, log로 인해 곱셈이 합으로 표현 가능해집니다. 그리고 pθ 식을 베르누이 식으로 변형한 뒤 정리하면 cross-entropy식이 나오게 됩니다.

2) Gaussain Distribution
가우시안 분포를 따른다고 가정하면 μ와 σ값을 디코더가 내주고 가우시안 식으로 전개 후, σ=1(identity covariance)이라는 가정하에 squared Error로 표현이 가능하게 됩니다.

따라서 인코더 qϕ(z|x)는 가우시안 분포를 따르고, Reconstruction error의 식만 바꿔주면 두 가지의 VAE 구조를 만들 수 있습니다.

Reparameter Trick

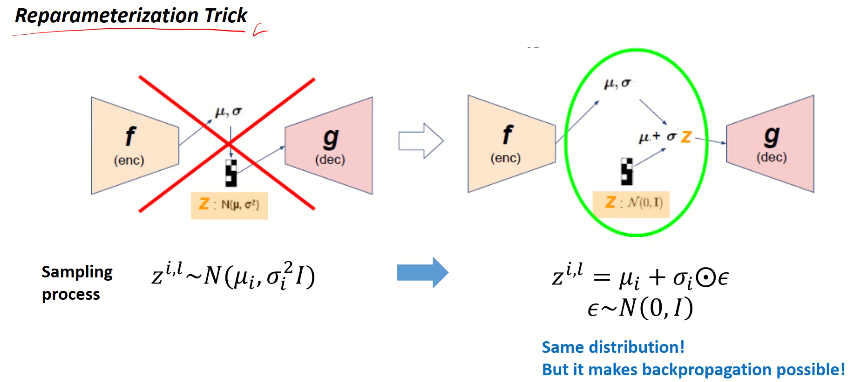
x가 가우시안 인코더로 들어가면, 뮤와 시그마를 output으로 뱉습니다. 여기서 이 뮤와 시그마를 통해 정규분포를 만들고, 여기서 z를 샘플링하는데 z 자체를 sampling한다면 random 연산은 미분이 불가능하기에 gradient backward가 불가능하게 됩니다. 그렇기에 reparameterization trick을 이용합니다.

reparameterization trick은 표준정규분포에서 입실론을 샘플링한 후에, 이를 인코더에서 나온 시그마와 곱하고 뮤를 더해 z를 만들어주는 것 입니다. 이렇게 만들어진 z는 뮤와 시그마로 표현이 가능하게 되어(z=μ+σㆍε : element-wise 곱) 미분이 가능하게 되고 back propagation이 가능하게 됩니다.

이렇게 만들어진 z가 디코더를 통과하면 원래의 input x값과 비슷하게 생긴 output을 복원시키게 됩니다.

최종 Structure Summary

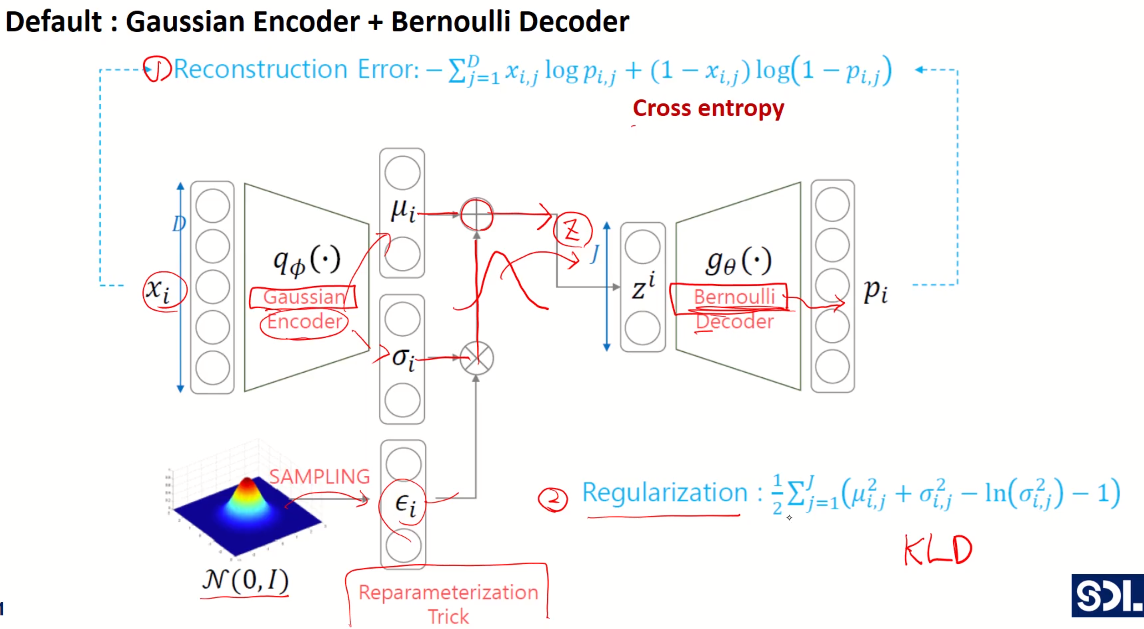
x가 가우시안 인코더로 들어가면, 뮤와 시그마를 output으로 뱉습니다. 여기서 z를 샘플링을 하는데 샘플링을 하는 것 자체는 미분이 불가하여 back propagation이 불가능합니다. 그렇기에 Reparameterization trick을 사용하여 표준정규분포에서 샘플링을 한 후에, 샘플링 한 값에 시그마를 곱해주고 뮤를 더해서 z를 만들어줍니다. 이렇게 만들어진 z가 (베르누이 or 가우시안) 디코더를 통과하게 됩니다.

베르누이를 따르는 디코더라면, p값이 나오게 되고(베르누이에서는 파라미터 값이 확률 p),
그렇게 되면 두 가지로 나뉘는 loss ft에서 Reconstruction error는 Cross entropy식이 되며, Regularization 식은 가우시안 인코더를 따르는 q가 normal distribution을 따르게 만드는 KL divergence를 쓰기 때문에 아래와 같은 식이 완성됩니다.

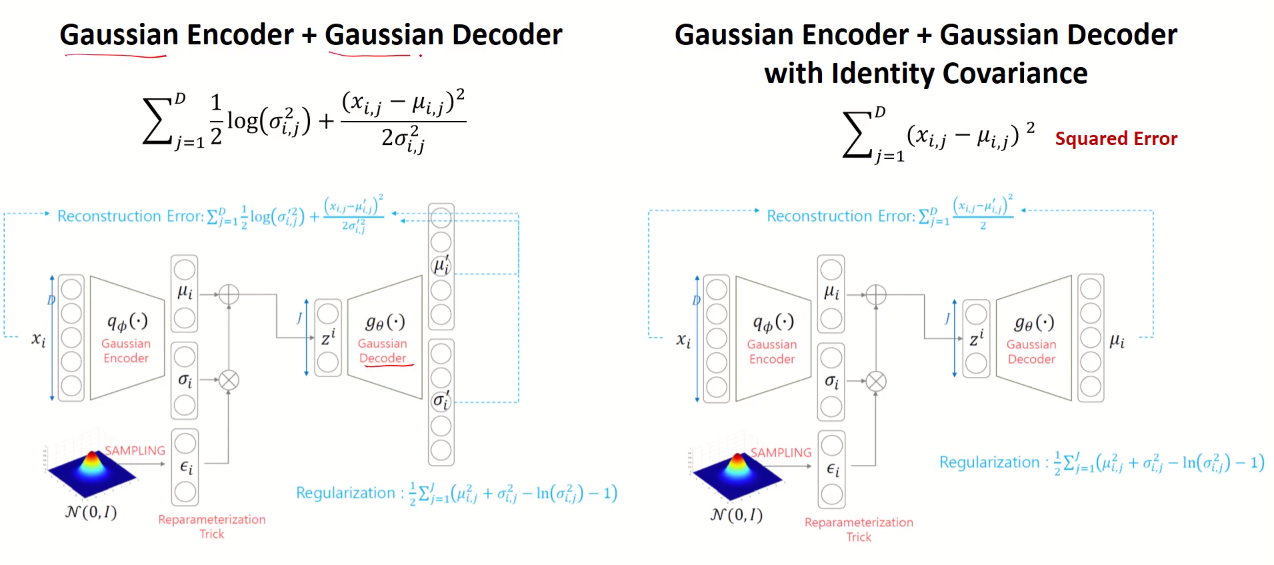
가우시안을 따르는 디코더라면, 위에서 Reconstruction error식만 바뀌게 됩니다. 여기서 시그마가 1인 단위행렬인 Identity Covariance인 경우 단순한 squared error식으로 바뀌게 됩니다.

Characteristics

잠재벡터의 차원을 늘릴수록 당연스럽게 원본 이미지와 유사해지는 것을 확인할 수 있습니다.

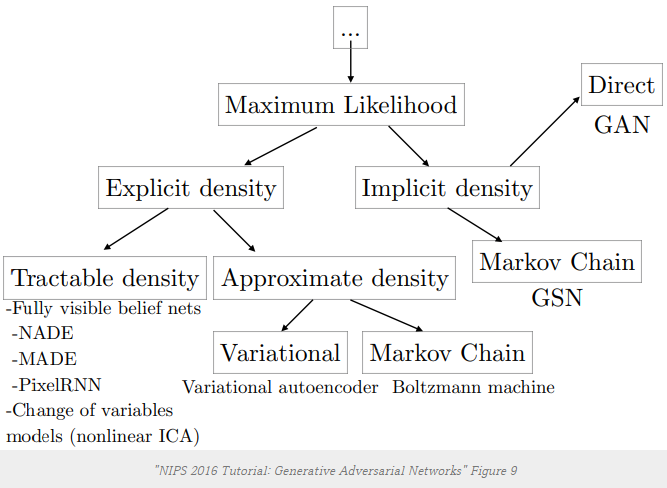
Experiments

MNIST 데이터셋 및 Frey Face 데이터 세트에서 이미지의 생성 모델을 훈련하고 ELBO및 Marginal likelihood 측면에서 학습 알고리즘을 비교하였는데, 잠재 공간이 바뀜과 상관없이 전체적으로 Marginal likelihood가 더 높게 나옴을 확인할 수 있습니다.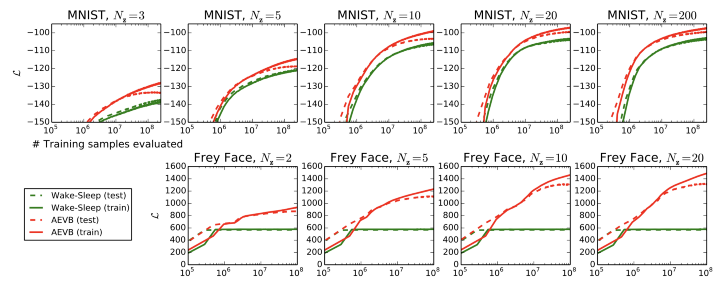
몬테 카를로 추정과 함께 dataset size에 따른 비교 또한 높은 marginal likelihood를 보였습니다.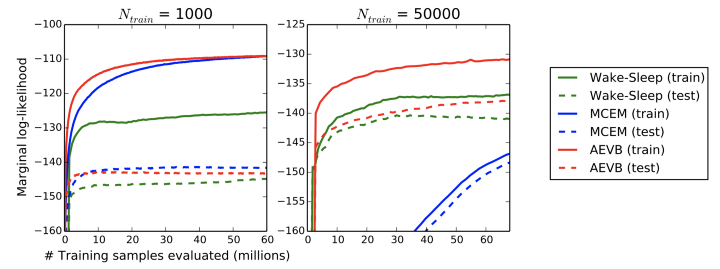

참고 : https://dongju923.github.io/paper/VAE/
https://aigong.tistory.com/367
https://judy-son.tistory.com/11
https://www.youtube.com/watch?v=GbCAwVVKaHY