몬테 카를로 알고리즘

몬테 카를로 알고리즘은 폴란드계 미국인 수학자 스타니스와프 울람이 제안한 알고리즘입니다.

이는 우리가 원하는 결과값에 대해 정확한 값을 얻는 방법은 아닙니다. 몬테 카를로 알고리즘은 무작위로 난수(랜덤 수)를 생성한 후, 무작위 난수를 기반으로 생성해서 구하고자 하는 결과값 즉, 원하는 정보의 확률값을 계산하는 알고리즘입니다.

난수 생성이 무한에 가까워질 수록 우리가 원하는 정보의 실제값으로 근사하게 됩니다.

이에 대한 대표적인 예시로 원주율 pi값을 근사하는 것이 있습니다.

몬테 카를로 알고리즘을 이용하여 pi값을 근사해보겠습니다.

아래와 같이 원이 있을 때, 이 원은 반지름이 1이라 가정하겠습니다.

이 원을 정확히 정사각형으로 4등분한다면, 그 중 하나는 아래와 같이 한 변의 길이가 1이고 부채꼴이 들어가있는 형태일 것 입니다. 이 부채꼴의 넓이는 우리가 알 듯이 pi/4일 것 입니다..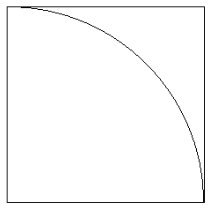
이 공간에 일정한 개수의 점을 균일하게 분포합니다. 그러면 아래와 같은 형태가 나오는데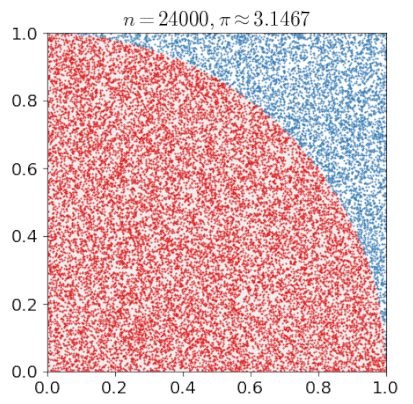
[ 사분원 내부의 점 개수 / 전체 점 개수 ] 를 구한 후 x4를 해준다면 이는 pi값에 근사해질 것 입니다.

여기서 중요한 점은 각 점들은 균일하게 분포되지 않으면 근사치가 떨어진다는 점과 평균적으로 더 많은 점을 배치할 수록 근사치가 개선된다는 점입니다.

몬테 카를로 알고리즘은 다양한 방법으로 접근이 불가능할 때 사용되며, 계산하려는 값이 닫힌 형식으로 표현되지 않거나 복잡한 경우에 근사적인 계산을 하기 위해 사용됩니다.