Hierarchical softmax : 계층적 softmax

Skip-gram model에서 softmax사용시에 계산 복잡성을 해결하기 위한 방법입니다.

만약 하나의 중심단어의 embedding 시에 100만개의 단어가 corpus에 있다면, 벡터의 내적을 100만번 진행해야 합니다. 이를 Hierarchical softmax는 이진 분류를 통해 log2(100만) (19~20사이의 값) 으로 계산량을 줄일 수 있습니다.

논문에서 소개되는 Hierarchical softmax는 아래와 같습니다.

예시를 들어보겠습니다.

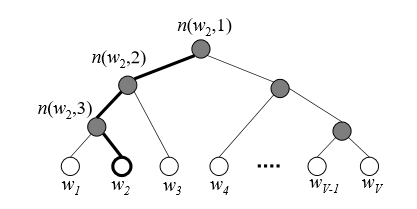
leaf node까지 가기 위해 거쳐가는 노드들은 각 벡터가 존재하며, 이 벡터들을 정답 leaf 단어가 있는 쪽으로 branch로 뻗어나갈 확률값을 최대화하도록 학습시키는 것이 목적입니다.
w4라는 단어의 주변부 단어가 w2일 때, 이 둘에 대한 확률값을 만들어야 합니다. 각 leaf mode까지 가는데 만나는 node에 해당하는 vector들을 내적해주고 sigmoid를 통해 확률값으로 만들어 준후 이들을 곱하여 leaf node로 내려갑니다. 최종적으로 나타나는 확률값을 최대or최소화 시켜주는 학습을 진행하여 parameter를 업데이트합니다.

결과적으로 softmax없이 sigmoid만으로 계산하게 됩니다.

식에서 [x]는 true이면 1, false이면 -1로, 좌측으로 내려가면 1, 우측으로 내려가면 -1이 선택됩니다. 그 이유로는 sigmoid함수의 특성 때문인데, σ(x)+σ(−x)=1 이기 때문입니다. 이로 인해 이진 분류로 뻗어나갈 수 있게 됩니다.

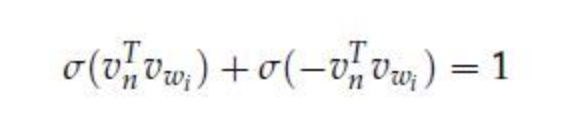
최종적으로 나온 leaf의 모든 확률 값의 합은 1이 되기에 확률분포를 이루며, 이 확률분포를 이용하여 일반적인 softmax와 같이 사용할 수 있게 됩니다.

예시2)

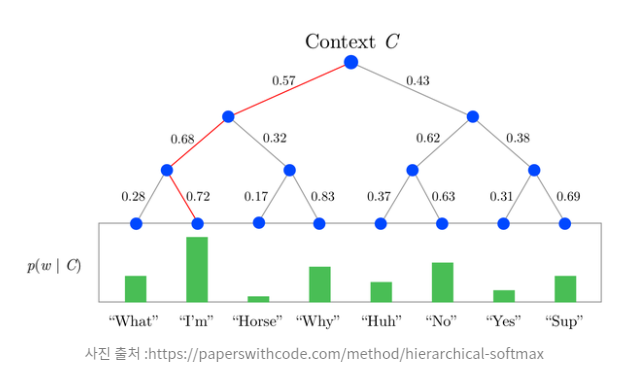
여기서 Context C가 들어왔을 때, I'm 이 나올 확률값은 아래와 같습니다.

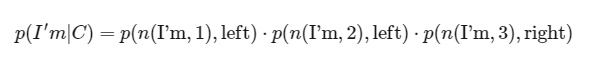
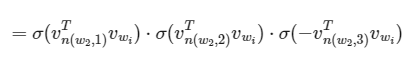
예시3)

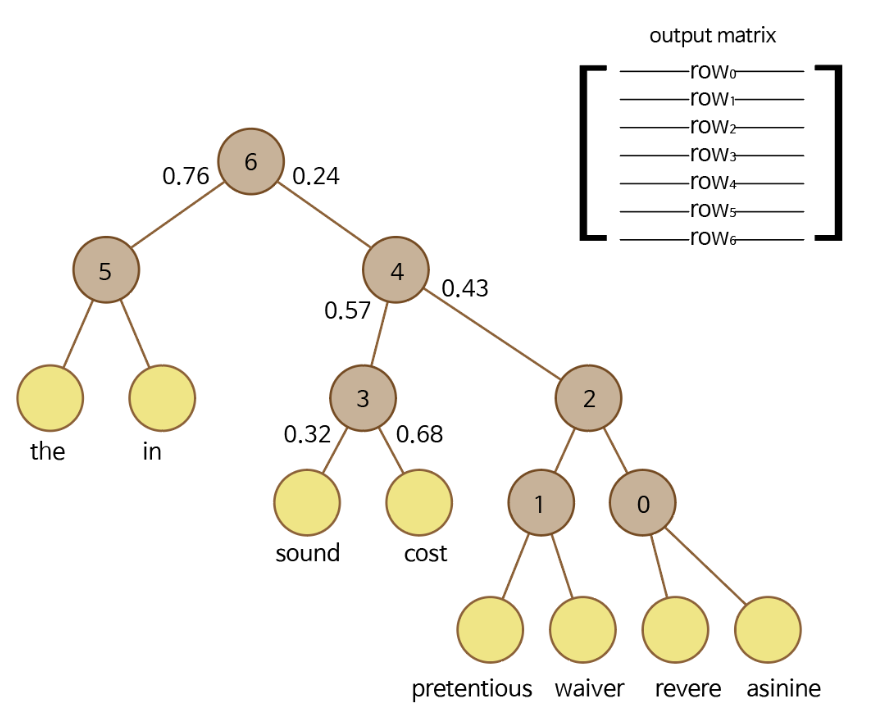
asinine을 입력했을 때 상황이라 가정한다면, asinine이 들어왔을 때, cost를 출력할 확률은 0.24 0.57 0.68 = 0.09324 가 됩니다.

이렇게 확률 값들을 구하고 W, W'을 업데이트 시켜 나가는 것 입니다!

참고 : https://uponthesky.tistory.com/15
https://velog.io/@xuio/NLP-TIL-Negative-Sampling%EA%B3%BC-Hierarchical-Softmax-Distributed-Representation-%EA%B7%B8%EB%A6%AC%EA%B3%A0-n-gram
https://real-myeong.tistory.com/78