이번 포스터에는 DQN의 변형들을 알아보겠습니다!
우선 Multi-step Learning에 대해 알아보겠습니다.
DQN의 loss ft을 보면 target에 rt+1이 있습니다. 하지만 게임을 할 때 바로 다음 step의 reward도 중요하지만 어떨 때는 10step이후까지 볼 수 있다면 더 좋을때도 있습니다.
따라서 이를 접목시킨 것이 Multi-step Learning입니다.
훨씬 더 앞으로 가서 타겟으로 삼습니다.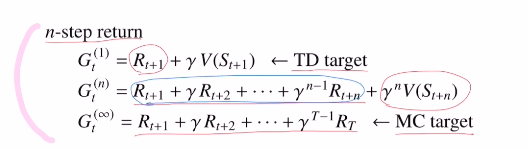
이제는 rt+1이 아닌 truncated n-step return을 사용합니다.
st+1이 아닌 st+n이 됩니다.
이번에는 Douvle DQN입니다.
Q learning에서는 max opreration이 존재하여 실제값보다 높게 측정이 되어 over estimate됩니다. 이를 해결하기 위해 douvle Q를 사용합니다.
하나는 action selection part와 하나는 action evaluation part로 나눕니다.
RL에서 Q network가 아닌 Q table을 사용하는데 여기서 Q table 2개를 사용하는 것입니다. 우선 Q1테이블에서 highest value를 갖는 action을 선택하고 이 action 을 Q1이 아닌 Q2테이블에 넣어 선택을 합니다. 이제는 Q2테이블에서는 maximum이라는 이유가 없기에 낮춰줍니다. Q1,Q2를 0.5의 확률로 업데이트 합니다.
모든 state action pair에서 일정 값만큼 같이 다 상승했다면?
이를 Uniformly overestimating 되었다고 하는데, 사실 이는 상관이 없습니다.
왜냐하면 애초에 Q값을 찾고자하는 것이 목표가 아니라 highest Q값을 갖는 action을 선택하는 것이 목표이기에 모두가 Q값이 올라가면 highest Q값은 똑같기 때문입니다.
하지만 강화학습에서는 모든 state action pair에서 값을 구하고 update를 하는 것이 아니기 때문에 일부분만 update가 됩니다. 그렇기에 여기서는 문제가 되는 것 입니다. 좋지 않은 policy가 됩니다.
Double DQN은 Double Q learning을 사용하여 overestimate를 낮추는 것 입니다.
DQN에서는 장점이 이미 두 개의 network가 있습니다.(behavior, target)
따라서 굳이 새로운 네트워크를 만들 필요가 없습니다.
이제는 behavior network에서 highest Q value를 갖는 action을 선택하고 target에 적용할 때만 바뀌었습니다. 이렇게 바뀐DQN은 action value acc와 policy quality가 더 좋아집니다.
이번에는 Prioritized Replay를 알아보겠습니다.
Experience replay에서 미니배치만큼 랜덤샘플링을 할 때 priority를 준다는 의미입니다.
Experience replay가 필요한 이유는 온라인으로 시간 순으로 받은 데이터를 바로바로 업데이트하여 strongly temporally-correlated upudates가 됩니다. 따라서 iid도 깨지고 성능이 많이 떨어지는 이 문제를 해결하고자 Replay buffer에 저장하고 미니배치만큼 학습하는 것 입니다. 또한 이로 인해 양이 적은 중요한 데이터를 기존과 다르게 바로 버리지 않고 반복적으로 사용할 수 있습니다.
Prioritized Replay는 Experience replay에서 랜덤샘플링 할 때 uniform하게 하는 것이 아닌, 중요한 것은 더 많이 학습을 할 수 있게 해줍니다. 즉, 사용할 transition에 priority를 주어 조금 더 자주 가져올 수 있게 해주는 것 입니다.
중요하다는 판단 기준은 무엇일까요?
-> Temporal difference error :TD error (pi를 이용하여 확률처럼 P(i)로 만듬) 를 통해 결정합니다.
이 에러가 큰 값을 중요한 것이라 생각하고 미니배치로 뽑을 때 더 많이 뽑힐 수 있게 확률을 올려줍니다.
여기서 샘플링할 때 uniform이 아닌 priority하게 샘플링하면
1) loss of diversity : 특정한 쏠림현상이 생기기에 다양성에 문제가 생깁니다.
-> stochastic sampling prioritization으로 해결합니다.
2) bias : importance sampling weights로 해결합니다.
두 문제가 생깁니다.
우선 Priority로 TD error를 사용하는 이유부터 알아보겠습니다.
강화학습이 아닌 Model based의 경우 value iteration을 생각해보겠습니다.
state value값을 계속 update하는데 어느 state을 먼저 업데이트할 것 인가는 기존에는 uniform하게 했지만 순서에 priority를 주면 성능이 많이 올라갑니다.
여기서 중요한 점은 어떻게 priority를 줄 것인가 입니다.
value iteration에서는 변화량에 따라 줍니다.
TD error가 state value 값의 변화량을 체크하는 좋은 방법중 하나이기에 이를 사용합니다.
model free인 강화학습에서도 마찬가지입니다.
로봇이 계속 넘어지다가 가끔 성공할 텐데 이 성공한 데이터가 아주 중요합니다.
이 transition이 중요하기에 replay buffer에서 더 많이 가져오고 싶은 것 입니다.
여기서 성공할 때 얻는 reward와 next state이 굉장히 좋은 것이 되는 것 입니다. 그 말은 current state가 있을 때 성공했다면 reward와 next state이 좋은 것이고, 그렇기에 pi값이 더 커지게 됩니다.
One ideal criterion : current에서 학습할 것이 더 많아지면 좋은 것입니다.. 즉, pi값이 크다.
따라서 TD error가 클 수록 중요하다고 생각하고 priotity를 주는 것 입니다!
또한 좋은 점은 이 TD error는 DQN을 학습할 때 loss ft의 gradient 를 구할 때 이미 구했던 값이기에 따로 추가적인 연산이 필요없는 것 입니다!

N개의 transition의 priority를 나타낼 수 있는 TD error값들을 갖고 있습니다.
미니배치가 200이라고 하면 N개 중 200개의 transition을 가져와 미니배치를 만들고 이를 통해 update할 때, TD error를 계산하게 됩니다. replay buffer안에 있는 미니배치들을 모두 TD error를 다시 계산하기에는 너무 많은 계산비용이 들기에 오직 미니배치로 사용된 200개의transition에 대해서만 TD error를 업데이트 합니다.
학습 초기에 TD error는 성능이 좋지 않습니다. 그렇기에 만약 TD error를 높은 값을 가지면 미니배치로 자주 샘플링됩니다. 그렇기에 계속 좋게 업데이트 됩니다. 하지만 초기에 낮은 값을 가지면 계속 뽑히지 않게 됩니다.
-> 이렇게 초기에 높은 값을 가지면 계속 뽑히고 반대면 뽑히지 않고, 이런 현상을 lack of diversity라고 합니다. 일부 데이터에 대해서만 학습이 되기에 over fitting이 발생합니다.
따라서 stochastic sampling prioritization 을 사용합니다.
이것은 알파값을 사용하는 것으로 만약 알파값이 0이면 1/N으로 모두 동일하게 random으로 뽑히게 됩니다. 기존의 uniform random sampling이 됩니다. 알파값이 1이면 priority를 최대로 적용한 것으로 위에서 언급했던 방식으로 lack of diversity가 발생할 위험이 있습니다.
이렇게 알파값을 (uniform) 0~1 (priority) 조절하여 샘플링을 진행합니다.
두 번째 문제는 random sampling할 때 priority가 계속 바뀌어 샘플링하는 distribution 자체가 계속 바뀝니다. 이로 인해 또 다른 bias가 생기는 것 입니다.
이를 보정할 수 있는 방법이 importance sampling weights이다.
이것을 통해 bias가 생긴 부분을 보정해줍니다.
만약 알파가 1이면 1/N로 unform하게 뽑습니다. 여기서 하나는 10/N이고, 하나는 0.1/N일 때, 앞의 것이 100배가 더 뽑힐 확률이 큽니다. 여기서 importance sampling weights를 찾으면 1 / Nㆍ(10/N) , 1 / Nㆍ(0.1/N) 이 됩니다.
이것을 파라미터를 업데이트 하기 전에 이를 곱하여 업데이트를 합니다. 둘 다 1/N 이 되어 1/N 효과를 냅니다. 이를 통해 non-uniform probablity를 배타가 1이라면 compensate시켜줍니다. 즉, 다시 unform으로 돌려줍니다.
따라서 Gradient Descent를 할 때, TD error에 이 wegiht를 곱하여 적용하여 parameter를 update합니다. 하지만 여기서 stability에 문제가 생길 수 있기에 wk의 maximum 값으로 나누어 normalize를 시켜줍니다.
학습이 거의 끝날 때는 converge가 거의 다 된 상태이기에 bais가 심하면 문제가 됩니다. 따라서 이 때는 unbiased update가 아주 중요합니다. 그래서 베타를 거의 1로 바꿔줍니다. 초반에 베타가 초기화되면 학습을 진행시킬 수록 점점 1에 가깝게 바꿔가는 것 입니다.
마지막으로 Double DQN에 priority replay를 적용한 수도코드를 확인해보겠습니다.
highest Q value를 갖는 action을 선택할 때, target network가 아닌 behavior network에서 다뤘습니다.
우선 하이퍼파라미터는 미니배치크기, replay buffer 크기, stochastic sampling에 사용될 알파, importance sampling을 할 때 사용될 배타 를 정해줍니다.
초기 replay buffer을 N으로 둡니다.
current state st가 오면 behavior network에서 highest Q value를 갖는 action을 선택해줍니다. 여기서 ε-greedy를 사용합니다.
이 action을 가지고 emulator(환경)에 실행시켜서 immediate reward rt+1과 next state st+1을 얻습니다.
(st,at,rt+1,st+1) 을 얻고 replay buffer에 저장합니다.
이제는 priority도 저장해야하기에 TD error를 저장해야 하는데, 굳이 지금할 필요는 없고 뒤에서 계산하여 저장합니다.
우선 이 transition은 가장 최신 데이터이기에 maxpi로 가장 많은 priority를 우선 줍니다.
t가 K일 때 이를 실행합니다.
: replay buffer에 1개 튜플 넣고 바로 미니배치만큼 꺼내어 학습하는 것이 아닌,
K개 만큼 넣고 그 다음에 미니배치만큼 꺼내어 학습을 합니다.
미니배치만큼 샘플링을 하는데 priority를 따라 샘플링을 하고, 샘플에 대해 importance weight 를 계산해두고, TD error를 계산하게 됩니다. TD error를 계산할 때는 Double DQN을 사용합니다.
TD error값을 업데이트합니다.
이를 통해 Gradient descent에서 앞에 weight와 곱해주어 파라미터를 업데이트합니다.
반복하다가 특정 step에서 target network에 copy를 통해 바꿔줍니다.
고려대학교 오승상 교수님 강화학습 : https://www.youtube.com/watch?v=hjXbfFeY1Ac&list=PLvbUC2Zh5oJtYXow4jawpZJ2xBel6vGhC&index=19
