지난 포스터까지는 Deep Reinforcement learning으로 DQN, REINFORCE, A3C를 알아보았다면, 이번 포스터부터는 Policy Gradient DRL으로 DDPG, TRPO, PPO에 대해서 알아보겠습니다!
Deep Deterministic Poilcy Gradient: DDPG 를 알아보겠습니다.
지금까지 policy는 stochastic이었지만, 여기서는 Deterministic policy를 사용합니다.
DQN은 finite한 action space에서만 작동하기에 robotics에는 적용할 수 없었습니다.
conti action space에서는 discrete하게 finite개로 줄일 수 있습니다.
(ex) 로봇 관절의 각도(infinite)를 10도 단위로 나누어 사용)
이를 discretization이라고 합니다. 하지만 이렇게 되면 관절이 12개이며 각도가 90개면 총 90^12개의 action이 있는 것 입니다. 이러면 다룰 수 없게 됩니다.
이 문제를 curse of dimensionality라고 합니다. 관절의 각도의 개수를 너무 줄이면 정보를 잘 활용할 수 없습니다.
따라서 모델의 action이 섬세한 것을 요구하면 discretization은 쉽지 않습니다.
DQN의 문제를 해결하기 위해 Policy Gradient알고리즘을 알아보았습니다.(A3C)
이를 해결하기 위해 또 다른 방법으로 오늘 알아볼 DDPG가 있습니다.
이제는 conti action space에서 actor는 랜덤성이 없는 deterministic policy를 사용하고, critic에서는 Q ft을 사용합니다.
DDPG에서는 Q ft을 학습하기에 용이한 DQN을 사용합니다. 그렇기에 experience replay와 target network로 그대로 사용합니다.
DDPG의 어려운 점은 performance가 monotonic하게 improve되지 않는다는 점입니다.
우선 Deterministic Policy Gradient DPG를 알아보겠습니다.
policy gradient 알고리즘은 policy gradient thm을 기반으로 이론이 시작되었습니다.
이 때는 stochastic이었지만, 이제는 deterministic입니다. 따라서 deterministic policy gradient thm을 기반으로 합니다.
stochastic은 확률이기에 파이로 표현함과 달리 deterministic은 고정된 값(action)이기에 뮤라고 표현합니다.
stochastic은 state 과 action 에 대한 π(a|s)로 표현되지만 deterministic은 μ(s)로 state이 하나 결정되면 action이 자동으로 결정되기에 state 의해서만 결정되는 함수가 됩니다.
당연히 deterministic이 훨씬 더 적은 샘플로도 approximate할 수 있습니다.
우선 파라미터 업데이트를 위한 gradient를 이해하기 위해 state visitation frequency를 알아보겠습니다. 말 그대로 특정한 state을 방문할 frequency입니다. frequency는 확률은 아니지만 비슷한 형태를 취할 때 사용합니다.(방문할 확률이 높다 정도로 이해하시면 될 것 같습니다)
policy가 고정되어 있기에 주어진 policy에 따라 여러 에피소드를 얻게 됩니다.
이 중에서 특정한 state에 얼마나 자주 방문할지를 알아보는 것 입니다. 이것이 ρπ(s) 입니다.
공식을 보면 policy가 주어졌을 때, 모든 time step t에서 주어진 state s에 있을 확률을 더한 것을 말합니다. 각 time step마다 discounted factor를 곱해줍니다.
오른쪽 식은 s'에 있을 확률과 s'이라는 state에서 시작했을 때, time step t 이후 s에 올 확률을 곱한 것을 sumation한 것 입니다. 모든 s가 초기값이 될 수 있기에 integral을 통해 sum해줍니다.
모든 로우의 sum을 하면 안으로 들어오고 1이 되기에 총 1/1-감마 가 됩니다.
이 때는 로우에 (1-감마):constant factor를 곱하면 sum하면 1이기에 확률이라고 할 수 있습니다.
state visitation frequency를 이용해서 deterministic policy gradient를 증명해서 gradient식을 증명해보겠습니다.
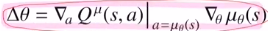
여기서는 Q value ft의 expectation을 목적함수로 하겠습니다.
state이 state visitation frequency을 따릅니다.
이제는 action은 정해지는 것이기에 Q value ft은 state으로 정의되는 함수입니다.
그렇기에 state에 대해서만 적분합니다. (Q는 함성함수입니다!)
목적함수의 gradient를 취하겠습니다. action에는 세타와 관련이 있기에 chain rule을 통해
Q 함수를 action에 대해 미분하고, action인 뮤를 세타에 대해 미분한 것을 곱해줍니다!
그리고 expectation으로 변형하여 최종 gradient를 구해줍니다.
이번에는 DDPG에 대해 알아보겠습니다.
critic에서는 Q ft을 학습하고, actor에서는 deterministic policy를 학습합니다.
따라서 conti action space까지 control할 수 있게 됩니다.
DDPG는 Q ft을 사용하기에 DQN을 사용합니다.(experience replay와 target network를 사용합니다.)
loss ft은 TD error를 사용합니다. target과 behavior net Q 값을 구분합니다.
DDPG에서는 actor net과 critic net이 각각 target용이 있고, behavior용이 있습니다.(4개의 파라미터가 있습니다.)
목적함수는 동일합니다.
4개의 네트워크는 같은 structure을 공유합니다.
stochastic은 확률적으로 optimal이 아닌 부분도 경험하며 exploration이 보장됩니다.
하지만 deterministic은 정확히 동일한 한 개의 action만을 추출합니다. 따라서 exploration이 보장이 되지 않기에 noise를 첨가하여 더 나은 action의 exploration을 만들어 줍니다.
DQN과 달리 이제는 conti action space이기에 noise를 주어 약간 움직이게 하는 (ex) 관절 15도 인데 noise로 15.3도 움직이게) 방법을 사용합니다. 이렇게 exploration을 첨가합니다.
(각 step마다 다른 noise를 줍니다.)
기존 DQN에서 c=100이라고 하면 behavior net을 100번 업데이트하고 target net의 값을 바꿔주었습니다. 하지만 여기서는 Soft update를 사용합니다. 이제는 조금씩 조금씩 1/100 만큼 바꾸는 것 입니다.
마지막으로 DDPG의 수도코드를 확인해 보겠습니다.
DQN의 수도코드와 비슷합니다.
behavior : ciritic, actor
target : ciritic, actor
에피소드가 시작할 때 action exploration을 주기 위해 random noise process N을 초기화합니다.니다.
highest policy가 아닌 이제는 deterministic policy를 적용했습니다.
actor network를 통해 action을 선택하고 noise를 첨가합니다.
이를 통해 immediate reward와 next state을 얻습니다.
이 4 tuple을 replay buffer에 저장합니다. 여기서 미니배치만큼 샘플링하고 target을 계산합니다. target actor net에서 계산하고, target critic net에서 계산합니다.
이렇게 target이정해지면
loss ft을 minimize하는 방향으로 ciritic net을 업데이트 합니다.
actor net도 deterministic policy gradient를 통해 업데이트 합니다.
여기서는 soft update를 하기로 했기에 일정비율로 나누어 업데이트를 진행합니다.
이런식으로 반복하여 에피소드 전체에 대해 behavior, target net을 업데이트하게 됩니다.
고려대학교 오승상 교수님 강화학습 : https://www.youtube.com/watch?v=Ukloo2xtayQ&list=PLvbUC2Zh5oJtYXow4jawpZJ2xBel6vGhC&index=26
