이번 포스터에서는 Trust Region Policy Optimization: TRPO에 대해 알아보겠습니다!
DDPG는 conti action space에서 다룰 수 있다는 장점이 있었습니다. 이를 다루기 위해서 stochastic이 아닌 deterministic policy 뮤를 사용했습니다.
단점으로는 performance의 monotonic하게 improve함을 보장할 수 없었습니다.
목적함수의 단조 증가를 보장할 수 없기에 이를 해결하기 위해 TRPO를 도입합니다.
TRPO는 두 개의 컨셉을 가지고 있습니다.
1) Minorization-Maximization algotithm
2) Trust region
policy net에 있는 파라미터 세타를 업데이트 하는데 expected return을 maximizing하는 방향으로 업데이트 합니다. trust region 안에서 policy parameter를 업데이트 하면 monotonic이 보장됩니다! policy parameter세타는 policy space에서 움직입니다.
여기서 KL-div를 이용해서 제약조건을 만들어 trust region을 만들게 됩니다.
이렇게 되면 object ft인 expected return이 monotonic하게 improve함을 보장합니다.
이전에는 DDPG의 step size를 잘 조절해주어야 했지만, 이제는 보장이 되기에 많이 고려할 필요가 없다는 장점이 있습니다.
본 논문의 저자들은 monotonic improvement에 대해 이론적으로 증명을 한 알고리즘을 소개합니다. 이론적으로 잘 정립되어 있지만, practical한 알고리즘으로 구현하기 위해서 여러 번의 appoximate를 진행합니다. 이 과정을 이후 내용에서 잘 살펴보겠습니다.
TRPO는 성능이 상당히 좋지만, 복잡하기에 policy net이 커지면 거의 계산을 감당할 수 없게 됩니다. 큰 size의 CNN, RNN을 다루기 어렵습니다. 따라서 여러 번의 approximate를 해야 하며 이 사이에서도 많은 양의 계산이 요구된다는 점에서 어렵습니다.
우선 trust region이 왜 필요한지 알아보겠습니다.
Intuition
곡면의 optimal 길을 찾고 싶습니다. 바로 옆에 낭떠러지가 있기에 조심해서 올라가야 합니다.
단순히 gradient를 구해서 가면 위험이 높습니다. 얼마나 가야 하는지는 알기 어렵습니다.
=> 그렇다면 오른쪽 사진과 같이 믿을 수 있는 안전한 구역(trust region)을 알 수 있다면 어떨까요?
이렇게 된다면 마음 놓고 gradient를 구해서 이 원 내부에서 최적의 길로 이동할 수 있게 됩니다.
step size의 적절한 range를 잡기 어렵기에 trust region을 만듦으로 이 내부에서 policy를 업데이트 하게 됩니다. 이를 통해 improvement를 항상 보장할 수 있고 반복적 적용을 통해 optimal에 도달하게 되는 것 입니다!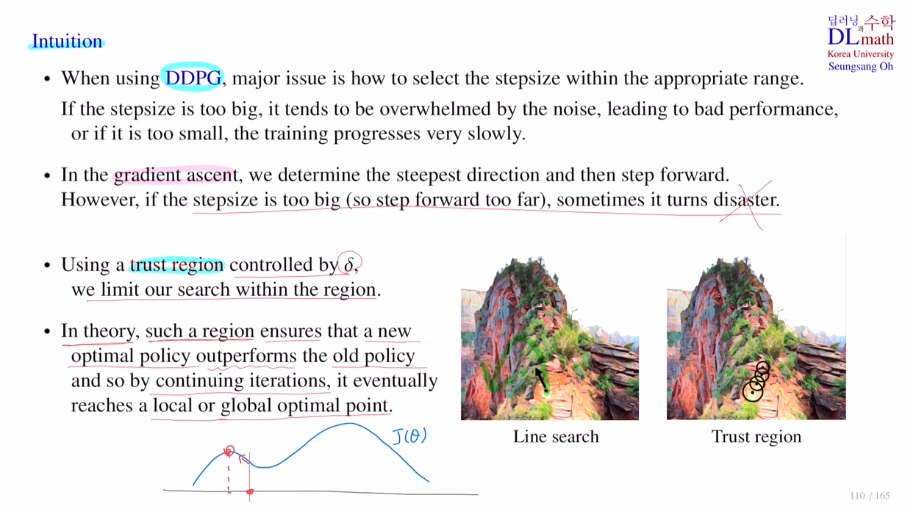
이제는 TRPO알고리즘을 어떻게 만드는지 단계적으로 살펴보겠습니다.
가장 중요한 부분은 목적함수 입니다.
(DDPG에서는 목적함수를 Q ft의 expectation으로 했습니다.)
에피소드 하나에 대한 return값이 있고, 이것을 주어진 policy에 의해 만들어진 모든 에피소드에 대해 expectation을 취한 것을 목적함수로 둡니다.
이 목적함수를 maximize하는 방향으로 학습합니다.
new policy에 대한 expected return인 η(π)가 있습니다.
이것은 기존에 사용했던 old policy에 대한 에타값을 이용해서 new policy에 대한 에타값을 계산합니다.
아래의 증명을 통해 new policy에 대한 에타값은 old policy에 대한 에타값에 뒤의 term을 더해주어 계산하게 됩니다.
여기서 고민할 점은 new policy에 대한 에타값은 old policy에 대한 에타값 보다 항상 큰지에 대함입니다. 다시 말해, 뒤의 term이 0보다 큰가? 입니다. 우선 로우는 확률값이기에 항상0보다 큽니다. 따라서 모든 state에 대해 action에 대한 시그마 값이 0보다 크면 되는 것 입니다.
하지만 approximate할 때 몇몇 state에서 음수가 나올 수도 있습니다. 따라서 현재는 보장할 수 없기에 차후 위에서 언급한 trust region으로 해결해줍니다.
new policy를 구하는 과정에서 new policy는 state visitation frequency와 관련이 있는데, state visitation frequency를 찾기 위해서 new policy에 대한 샘플들도 많이 구해야 합니다. 그렇기에 optimize하는 것은 상당히 어렵습니다. 그렇기에 policy를 old policy로 바꿔주게 됩니다.
이제는 old policy를 사용하기에 policy가 업데이트 되어도 state visitation frequency가 바뀌는 것은 무시해도 되는 것 입니다!
에타가 있을 때, L을 이렇게 바꿔주는 것 입니다. 이것은 local arpproximate가 됩니다.
이렇게 되면 인근에서는 굉장히 유사하게 되기에 L은 에타의 좋은 approximation이 됩니다.
A(s,a) = Q(s,a) - V(s,a)인데 = Q(s,a) - Ea[Q(s,a)] 입니다.
여기 전체에 expectation을 취하면, Ea[A(s,a)] = Ea[Q(s,a) - Ea[Q(s,a)]] = 0이 됩니다. 그렇기에 old policy에서 같은 값을 가질 뿐 아니라, 여기서 같은 기울기도 가집니다!
따라서 old policy로 바꾸어도 상당히 근사한 approximation이 되는 것 입니다.
하지만 작은 step에서는 보장되지만, 큰 step에서는 보장되지 않습니다.
이제는 이렇게 old policy를 썼을 때, L의 최대가 되어도 에타에서는 좋지 않게 나올 수도 있습니다. 그렇기에 conservative policy iteration update를 사용합니다.
알파를 통해 일부분에 대해서만 new policy를 적용하겠다는 것 입니다.
이렇게 조절하여 조금만 이동하게 바꿔줍니다.
L값에 어떤 값을 빼주면 그것은 에타의 lower bound를 보장해줍니다. 알파값이 커진다는 것은 더 많이 이동하기에 오차가 커짐을 표현해 주었습니다. 또한 discoutn factor가 1에 가까워지면 time step이 지남에 따라 discount를 많이 시키지 않는다는 의미이고, 그런 경우는 lower bound가 더 안 좋아집니다. 입실론을 구할 때 new policy에 대해서 다루기에 어렵습니다. 이렇게 이론적으로는 좋지만 mixture policy를 적용하는 것은 practical하게 사용하기 어렵습니다. 
고려대학교 오승상 교수님 강화학습 강의 : https://www.youtube.com/watch?v=c15b9AjHxBA&list=PLvbUC2Zh5oJtYXow4jawpZJ2xBel6vGhC&index=27
