Distributional Reinforcement learning을 사용한 C51을 알아보겠습니다!
Categoricla DQN이라고도 합니다.
기본 아케텍쳐는 DNQ을 따르고 있고, distribution을 출력하는데 categorical하게 본다고 해서 categorical DQN이라고 부릅니다. 51은 support의 개수를 말합니다.
C51은 Parameterization, Bellman update, Projection 이 세 가지가 핵심입니다.
1) Parameterization
Z라는 true 분포를 discrete 분포로 만드는 과정입니다.
여기서 discrete로 만들 때, finite fixed support를 사용합니다.
Diracs ft 앞에 확률값(learnable probability)을 주어 support의 개수만큼 sumation해주는 것 입니다.
확률은 learnable로 학습을 하는데 학습하는 과정이 softmax를 사용합니다.
적당한 확률분포 Z가 있을 때 각각 값은 return이라고 하겠습니다.
return의 하한과 상한을 주고, 균등한 간격으로 나누겠습니다. 이렇게 discrete하게 support로 나누겠습니다. dirac ft도 정의하겠습니다.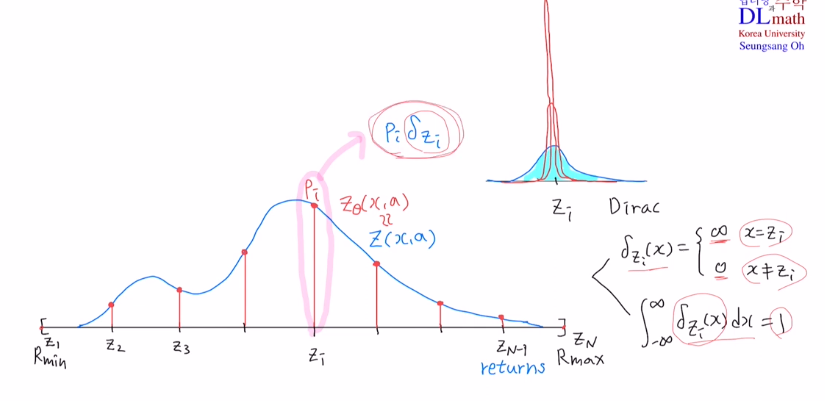
C51의 단점은 bound를 정하는 것 입니다.
DQN과 달리 이제는 action에 따른 Q값이 아닌 actin에 따른 분포를 출력해야 합니다.
분포는 discrete로 나누었기에 support개수를 N이라고 한다면 총 action개수 x N 개 를 output으로 내보내는 것 입니다. 여기서는 pi인 확률을 학습하게 됩니다.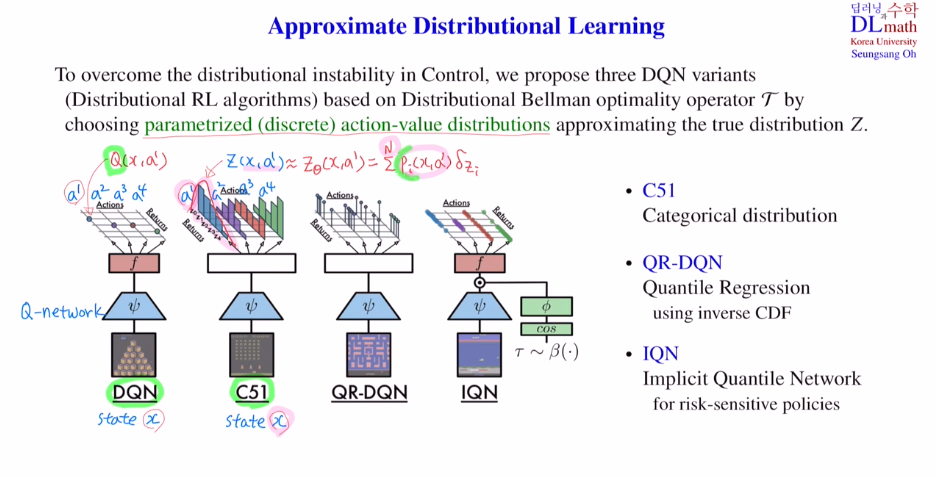
pi는 확률이어야 하기에 network의 output으로 Θi들이 나올 텐데 여기에softmax를 취해 pi를 만듭니다.
2) Bellman update
Q value ft을 maximize하는 action을 선택하고, Z를 적용하고 discounted factor를 곱한 후 immediate reward를 더하여 target을 표현했습니다.
target에서 구한 값이 있고, behavior에서 구한 값이 있으면, 이 사이를 비교할 텐데 discrete를 사용했기에 두 분포는 support가 다를 수 있습니다!
분포가 있을 때, discrete로 바꾸고 discount factor를 곱하면 0을 중심으로 옆으로 줄어들게 됩니다. 그리고 immediate reward를 더하면 우측으로 이동하게 됩니다. 그것이 operator를 통해 얻어진 ZΘ가 됩니다. 이제는 벨만 업데이트를 하기 전과 이후 분포를 비교하겠습니다.
새로 얻은 분포의 support는 변화되어 있습니다.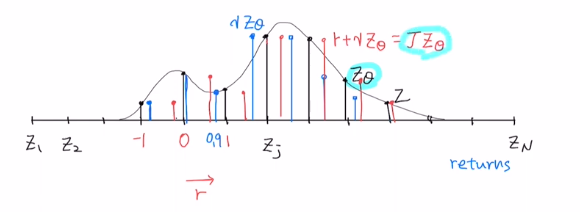
따라서 support가 다른 경우가 많은 데 Wasserstein metric은 두 분포의 disjoint suppot이슈가 크게 문제가 되지 않습니다. 하지만 Wasserstein metric을 사용하면 미분이 불가하기에 SGD를 사용할 수 없습니다. 또한 control part에서 distributional instability문제가 있었습니다. 따라서 Wasserstein metric보다는 미분이 가능한 KL-idv를 사용하고 싶습니다.
하지만! 또 KL-div를 쓰기에 disjoint support issue가 해결되어야 합니다.
따라서 target에서 얻어진 분포를 기존 support에 맞게 수정을 하게 됩니다.
3) Projection Φ
첫 번째 방법은 target분포를 잘 설명하는 smooth분포를 찾은 후 주어진 support에 맞게 찾는 것 입니다. 하지만 smooth분포를 찾을 수 없기에 다른 방법을 사용합니다.
target값에서 기존 support를 기준으로 길이 비를 나누어 target 확률값을 비례하게 잘라 각 가까운 support로 옮겨주게 됩니다. 이렇게 큰 것은 가까운 쪽으로, 작은 것은 먼 쪽으로 쌓아줍니다. 이 방법을 Projection Φ이라고 합니다. 이를 통해 KL-div를 사용할 수 있게 됩니다.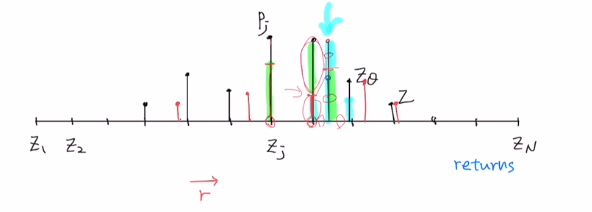
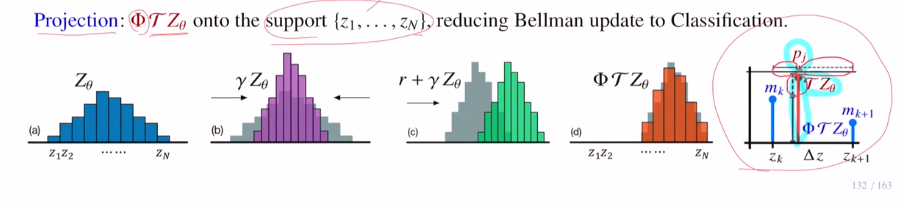
이렇게 Wasserstein metric은 이론적으로 좋지만, practical하게 사용하기 어렵다는 점으로 인해, 미분 가능한 KL-div를 쓸 수 있도록 Projection을 통해 분포를 바꾸어 disjoint support issue를 해결하였습니다.
다음 포스터에서 알아볼 QR-DQN은 Wasserstein metric을 사용할 수 있게 변경하기도 합니다.
이제는 SGD를 사용할 수 있습니다. behavior분포의 파라미터인 Θ에 대해서만 업데이트합니다.
따라서 KL-div를 minimize하는 방향으로 학습하는 것이나, 아래의 정리한 식에서 앞 부분은 상수취급이 되기에 cross entropy를 minimize하는 방향으로 학습하는 것이나 같게 됩니다!
DQN에서 Q 대신 Z, Z 대신 discrete, loss ft을 cross entropy로 바꿔준 것 입니다.
나머지 부분은 유사하고 아래 형광 부분만 변화하게 됩니다.
우선 replay buffer에서 minibatch를 샘플링 해서 가져왔습니다. 그리고 이 샘플을 가지고 network를 통해 action value 분포를 discrete 버전으로 계산합니다. 그리고 expectation을 취하면 Q값이 되고 이 Q를 maximize시키는 action a를 선택합니다.
기존의 return값들 각각에 대해 target값을 계산합니다.(return에 대해 discount를 곱하고 immediate reward를 더합니다)
projection을 적용해줍니다.(비율을 가지고 잘라 support에 더해줍니다.)
이렇게 나온 것과 기존의 분포를 원래는 KL-div로 미분하고 계산해야 하지만, cross entropy를 통해 계산을 해줍니다. 이를 minimize하는 방향으로 학습하게 됩니다.
고려대학교 오승상 교수님 강화학습 강의 : https://www.youtube.com/watch?v=xsLqA8a1Be4&list=PLvbUC2Zh5oJtYXow4jawpZJ2xBel6vGhC&index=32
