이번 포스터부터는 Distributional Reinforcement Learning에 대해 알아보겠습니다!
대표적인 알고리즘은 C51, QR-DQN, IQN이 있습니다.
Distributional Reinforcement Learning의 기본 개념들을 알아보겠습니다.
Distributional RL은 reward의 randomness에 초점을 둡니다.
trajectory가 있다고 할 때, state(transition probability를 따름), action(stochastic policy를 따름), reward(특정 상수로 보았던 이전과 달리 확률분포로 이해 즉, reward를 random variable로 이해)에 랜섬성이 들어갑니다.
그렇기에 이제는 return값도 실수값이 아닌 distribution이 됩니다.
이 random return을 action-value distribution이라고 부릅니다.
Distributional Reinforcement Learning에서는 Q ft이 핵심이 아니라, action-value distribution을 사용하는 것이 핵심입니다.
벨만 eq는 Q ft을 기준으로 만들어졌습니다. immediate reward와 next state, next action의 Q value값에 discount를 하여 sum한 것을 expectation한 것이 벨만 eq였습니다.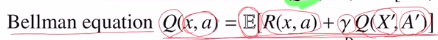
하지만 이제는 더 이상 Q ft을 사용하지 않고, Z ft을 사용하게 됩니다.
따라서 distributional Bellman equation을 아래와 같이 정의해줍니다.
모두 확률분포가 되었습니다. 이제는 expectation을 취하는 대신 distribution 자체를 비교하는 것으로 바뀌었습니다. 앞으로는 이 distributional Bellman equation을 이용해서 전개해 나가겠습니다.(여기서는 state 를 x로 표현합니다.)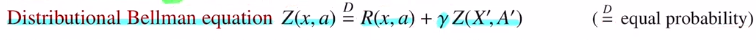
Policy evaluation는 원래 fixed policy에 대해서 Q value ft을 찾는 것 이었습니다. 이제는 operator라는 개념을 사용합니다. fixed policy에 대해서 distributional Bellman equation을 만족하는 Zπ를 찾는 것이 목적입니다.
Zk -벨만eq에 넣어 업데이트-> Zk+1 -벨만업데이트-> Zk+2
이 벨만 operator를 이용해서 distribute를 계속 업데이트합니다.
이렇게 했을 때 istributional Bellman equation의 가장 중요한 부분은 contraction한다는 것 입니다. contraction한다는 것은 operator에 의해 converge한다는 것이고 이를 통해 unique한 fixed pt: Zπ를 갖게 됩니다. 
Control part에서는 어떤 metric을 사용해도 contraction이 되지 않습니다. 심지어 conti도 되지 않기에 distributional instability가 생깁니다. 그렇기에 iteration의 convergence가 보장되지 않고, 또한 optimal action value distribution이 여러개 나올 수도 있습니다.
이것이 가장 어려운 문제입니다.
또한 Wasserstein metric이기에 GD알고리즘으로 계산이 불가합니다. practical하게는 더 어려운 문제가 됩니다. 따라서 discrete distribution으로 바꾸어 approximate를 하게 됩니다.
이것에 DQN을 적용한 것이 C51, 개선한 것이 QR-DQN, 또 개선한 것이 IQN입니다.
이제 Q ft대신 distribution을 사용하는데 이유를 알아보겠습니다.
기존에는 벨만 방정식을 사용할 때, Q값(return이 expected value)을 사용했습니다.
만약 return값이 stochastic으로 확률에 따라 여러 개가 나올 수 있다면, expected value를 통해 계산하게 됩니다. 하지만 이런 경우 suboptimal 결과가 나올 수 있습니다.
아래와 같이 pick 즉, mode가 정규분포와 달리 두개 있는 경우를 multimodal distribution이라고 합니다. 이 경우에는 suboptimal이 나올 수 있는 것 입니다.
아래의 경우들에서 return의 expectation값만 아는 것과 return의 distributiaon 자체를 아는 것은 큰 차이가 있습니다.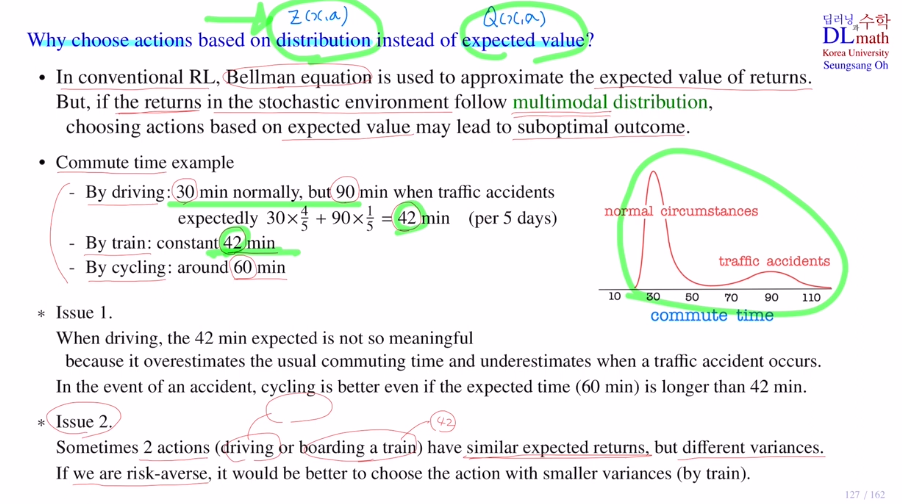
여기서는 Wasserstein metric을 사용한다고 했습니다.
두 확률분포의 거리를 잴 때, CDF를 통해 점 사이의 거리를 적분을 통해 값을 도출하는 방법입니다.
고려대학교 딥러닝(오승상교수님) - 43. Wasserstein GAN 1
을 참고하시면 좋을 것 같습니다.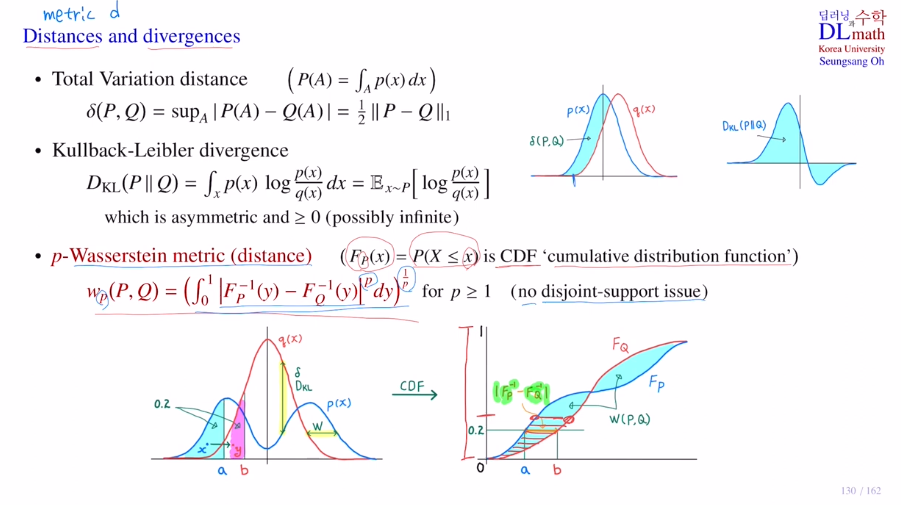
모든 (s,a)에서 벨만 eq를 만족하는 Q value ft을 찾는 것이 policy evaluation에서 해야 하는 것 이었습니다. 이제는 분포를 사용하기에 expectation을 사용하지 않습니다.
주어진 policy에 대해 모든 (s,a)에 대해서 distribution 벨만 방정식을 만족하는 Z파이를 찾아내는 것이 목표가 됩니다. 모든 (s,a)에 대해서 생각해야 하기에 이를 다루기 위해서는 operator를 사용하면 편리합니다. 따라서 operator를 사용하여 distribution 벨만 방정식을 다시 표현합니다. operator에 의해 fixed되는 Z파이를 찾게 되면 그것이 distribution 벨만 방정식을 만족하게 되고 궁극적으로 찾고 싶은 것이 됩니다.
모든 (s,a)에 대해서 Z1,2 분포의 거리를 찾고 싶을 때, 모든 (s,a)에 대한 Wasserstein metric의 supremum값을 구합니다. 그것을 바로 표현합니다. 이렇게 두 distribution사이의 거리를 표현합니다. 이것이 contraction이 된다는 것은 operator를 취한 값이 기존 값보다 항상 작거나 같다는 것 입니다.(두 분포의 거리가 가까워졌기에 좋습니다.)
이렇게 반복하며 감마가 계속 곱해지다 0으로 수렴하고, converge하게 되는 값을 Z파이라고 합니다.
Control part는 Bellman optimal equation을 사용합니다.
Q값도 optimal Q값입니다.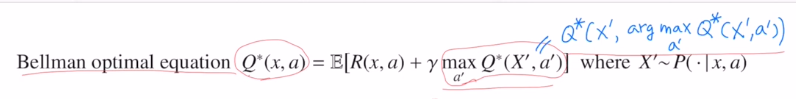
이를 distribution을 이용해 표현하면 아래와 같습니다.
마찬가지로 operator을 사용해 표현하는데 operator는 특정 policy와 상관이 없기에 파이를 쓰지 않습니다.
여기도 operator에 의해 fixed되는 Z가 있다면 그것이 optimal policy가 되는 것 입니다.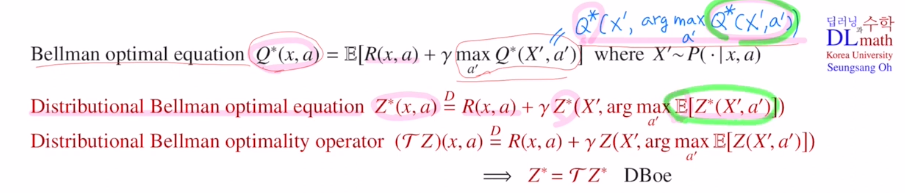
여기서도 점점 수렴하여 fixed pt를 가지면 좋겠지만, contraction하지 않습니다. 이를 distributional instability라고 합니다. 이것이 어려운 점입니다.
optimal이 여러개 나올 수 있는 데 이것을 expectation하면 Q 가 나오긴 합니다.
optimal Z 자체가 나오지 않을 수도 있습니다.
그나마 다행인 점은 unique optimal이 있다면, 그곳으로 converge한다는 보장은 있습니다.
이 문제들을 해결하기 위해 Approximate Distribution learning을 DQN과 사용하여 C51, QR-DQN, IQN이 등장하게 됩니다.
Approximate Distribution learning에서는 Control part에서 distributional instability문제와 policy evaluation part에서 Wasserstein metric을 사용해야 한다는 어려움이 있었습니다.
DQN에 input state이 들어오고 action이 4개 있을 때, Q net의 output은 각 action의 Q값입니다.
이것을 각 action별로 분포를 표현합니다. z(x,ai)
이것이 어렵기에 discrete 분포를 만들어 추정합니다.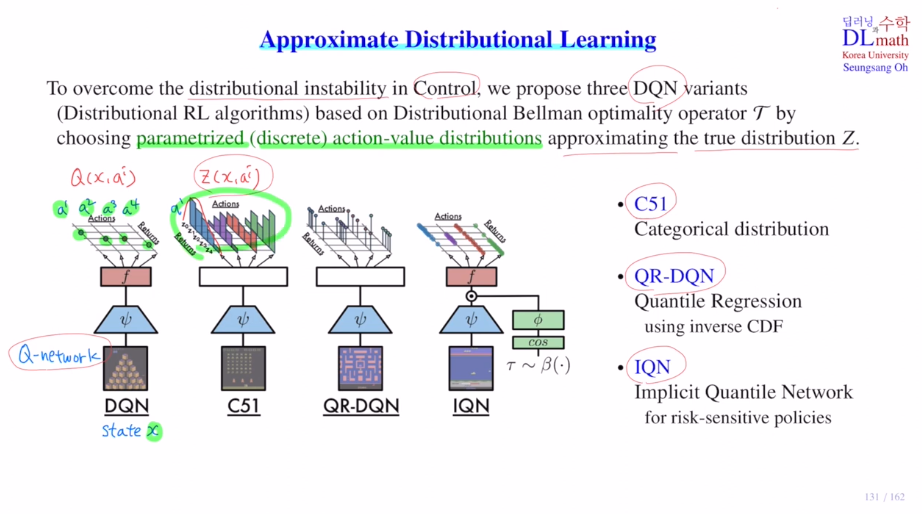
고려대학교 오승상 교수님 강화학습 강의 : https://www.youtube.com/watch?v=VYWdspLnhDE&list=PLvbUC2Zh5oJtYXow4jawpZJ2xBel6vGhC&index=31
