Dynamic programming 중에서 두 번째 방법인 policy iteration에 대해 알아보겠습니다.
이전 포스터에서는 value iteration에 대해 알아봤는데 bellman potimality eq를 이용하였습니다. 이를 만족하는 optimal state value ft V 을 찾고, value estimator를 이용한 점화식을 통해 converge 시키고 V 를 찾았습니다. 이 V 가 bellman optimality eq를 만족한다고 했습니다. 그 다음 V 을 통해 optimal policy π* 를 찾았습니다.
하지만 value iteration방법은 두 가지 단점이 있었습니다.
1) O(S^2A) per iteration & many iteratoins to converge
2) Vk(s) -> V* 하기 훨씬 이전에 policy가 더 이상 바뀌지 않아 이미 optimal policy를 얻을 수 있기에 굳이 끝까지 가는 것은 비효율적입니다.
이 단점을 개선한 것이 Policy iteration입니다.
이것은 bellman expectation eq를 사용합니다.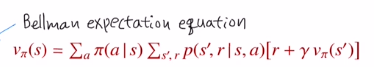
policy iteration은 policy evaluation:PE과 policy improvement:PI를 반복적으로 사용하며 이루어집니다.
1 policy evaluation:PE 정책 평가
value iteration과 비슷하지만, 여기서는 bellman expectation eq를 사용한다는 것이 차이점 입니다.
bellman expectation eq를 사용하기 위해서는 policy가 하나 정해져 있어야 합니다. 여기서 사용하는 것은 deterministic policy를 사용합니다. 즉, 하나의 state에 대한 policy가 action 단 하나로만 정해져있다는 것 입니다. : π(s)=a
value iteration에서는 sumation 앞에 maximization operation이 있었기에 모든 값들에 대해서 계산을 한 후 가장 큰 값을 취해야 했습니다.
하지만 여기서는 deterministic policy 하나에 대해서만 계산을 합니다. 즉, 하나의 fixed action에 대해서만 계산을 합니다. 따라서 훨씬 빠르게 계산을 합니다.
물론 여기서도 모든 state에 대해 계산을 해야 하기에 full backup을 사용합니다.
1) 모든 state에 대해 state value ft 초기화 2) 점화식을 통해 모든 state에 대해 계산을 하며 주어진 policy π에 대해 V를 converge시킵니다. 여기서는 이것이 optimal state value ft이 아니기에 끝난 것은 아닙니다. 단순히 여기까지 계산한 것 뿐. 여기서는 policy가 고정되어 있기에 하나의 action에 대해서만 계산하면 됩니다.
: O(S^2A) -> O(S^2)
2 policy improvement:PI 정책 개선
주어진 policy에 대한 state value ft Vπ를 기반으로 improve하여 new policy를 찾는 것 입니다. 여기서도 value iteration과 비슷하며 optimal V* 대신 Vπ가 들어갑니다. 이를 통해 new policy π'을 얻습니다. 하지만 Vπ가 optimal이 아니기에 π'도 optimal policy는 아닙니다.
하지만! 이 π'은 이전 policy보다 improve되었기에 더 좋다는 것이 특징입니다. 즉, 1 2를 반복하면 optimal policy π* 에 converge할 수 있다는 것 입니다!

-policy improvement Thm
π'은 Q를 argmax한 정책이기에 항상 크거나 같습니다. 그렇기에 π' is strictly better than π. 만약 둘이 같다면, 그 정책은 optimal policy가 되는 것 입니다.

아래는 policy iteration을 시퀀스처럼 표현한 것 입니다.
만약 MDP가 finte로 한정되어있다면 어느순간 멈추게 됩니다. 그것이 optimal policy가 됩니다.
Vπ=Vπ'이 되면 식 자체가 bellman optimality eq가 됩니다. 즉, 그것이 solution이 된다는 것입니다. 따라서 π'가 optimal이라는 말입니다.
수도코드는 아래와 같습니다.
state value ft, policy(각 state마다 random하게 action을 설정하여) 초기화
-> policy evaluation -> policy improvement -> new policy update 만약 같으면 그것이 optimal policy True로 바꾸어 stop loop
하나의 action에 대해서만 계산하기에 빠르고, policy update가 이루어지지 않으면 바로 stop하기에 value iteration보다 훨씬 효율적입니다.
greedy model 예시
k=3일 때 optimal policy 를 찾았습니다. 굳이 끝까지 갈 필요가 x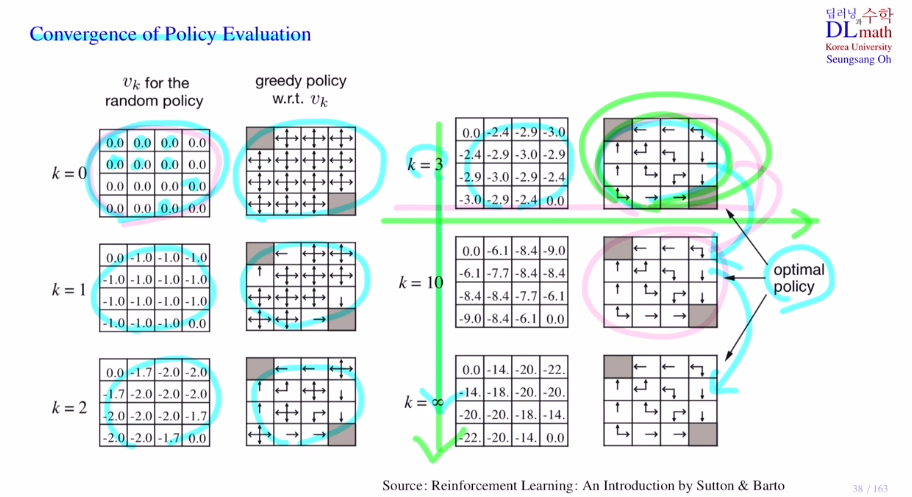
Dynamic programming에서는 bellman optimality eq을 풀어서 optimal policy를 찾는 것 이었습니다.
이를 위해서는 Markov property를 만족해야 했고, known MDP로 state transition prob과 같은 environment dynamics를 알고 있어야 했습니다. 테이블에 기록하기 위한 충분한 저장공간과 많은 계산 시간이 필요했습니다. full backup
(보통 백만개 state정도가 medium-sized)
Q를 계산하면 쉽지만 이것을 계산하는 것이 까다로워 주로 V를 계산.
curse of dimensionality : 차원의 저주로 state variables가 많아질수록 exponential하게 state의 개수도 많아집니다. 예를 들어 사족보행 로봇에서 각 다리마다 3개의 관절이 있다고 했을 때, 12개의 관절이 있는 것 입니다. 만약 각 관절마다 휘어지는 각도 state이 10가지가 있다고 하면 총 10^12만큼 state이 있게 됩니다.
(state variable:12, state:10^12)
이런 경우는 dynamic programming으로 문제를 해결할 수 없습니다.
따라서 이런 경우는 강화학습을 사용합니다.
각 iteration마다 모든 (s,a)pair가 아닌 얻은 샘플의 몇 개의 value ft만 업데이트합니다.
완벽한 정보는 아니기에 bellman optimality eq를 풀긴 하지만, approximation을 해서 풀게 됩니다.
하지만 이렇게 되면 샘플링을 사용하기에 더이상 차원의 저주에는 영향을 받지 않게 됩니다.
결국 미니배치에 depend하여 constant만큼 계산량이 요구됩니다.
고려대학교 오승상 교수님 강화학습 강의 : https://www.youtube.com/watch?v=6GhwCE43oFk&list=PLvbUC2Zh5oJtYXow4jawpZJ2xBel6vGhC&index=9
