이번 포스터에서는 Value iteration에 대해 알아보겠습니다!
Markov Decision Process문제를 해결하기 위해 나온 방법으로 DP와 강화학습이 있었습니다. Markov Decision Process문제를 해결한다는 것은 궁극적으로 optimal policy를 찾는다는 것 입니다.
DP를 사용하기 위해서는 MDP가 model based이어야 합니다. 그래야 state transition probability와 reward를 통해 모두 계산이 가능합니다.
DP의 대표적인 두 가지 방법은 value iteration과 policy iteration입니다.
차이점은 value iteration은 bellman optimality eq를 사용하며 policy iteration는 bellman expectation eq를 사용합니다.
오늘은 우선 value iteration을 알아보겠습니다.
value iteration은 bellman optimality eq를 사용한다고 했는데,
모든 state에 대한 optimal state value ft값을 찾은 후에 이것을 사용하여 optimal policy 를 찾습니다. 방정식의 solution을 어떻게 찾는지가 핵심입니다.
이 식을 만족하는 함수를 찾고 싶은데, state개수가 너무 많아 방정식을 푸는 것은 불가하기에 estimate로 추정합니다.
: Vk+1
이 점화식을 사용하여 반복적으로 optimal에 converge하도록 합니다.
bellman optimality eq를 Vk+1 점화식으로 바꾸어 Vk값이 converge 할 때까지 반복적으로 사용하여 V* 를 찾는 것이 핵심이 됩니다.
이 계산을 예를 통해 확인해 보겠습니다.
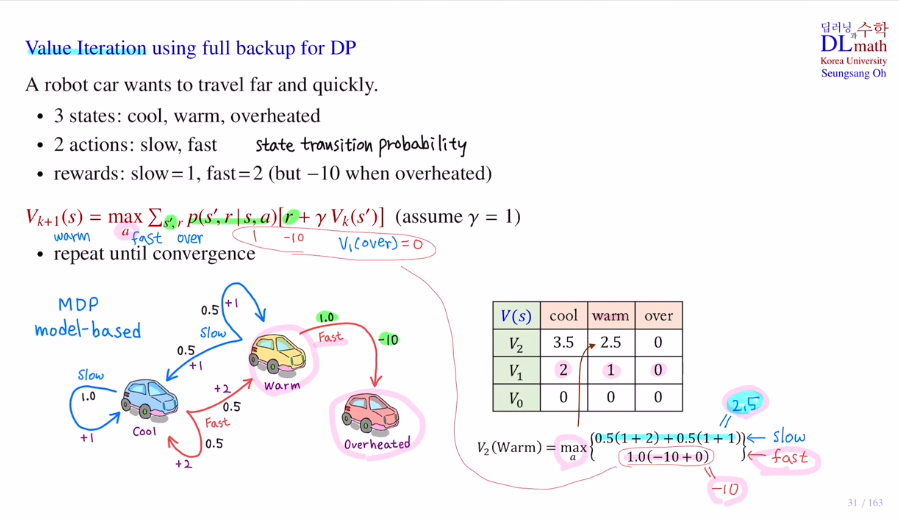
더 멀리 더 빨리.
여기서는 state transition prob가 나와있습니다. (discounted vector=1)
model-based
optimal state value ft의 estimator인 Vk라는 함수를 점화식을 통해 계산을 하고 update를 하여 어떤식으로 converge 하는 지 알아보겠습니다.
V0=0 으로 초기화
overheated는 no more action으로 no return입니다.
이것을 terminal이라고 하는데 값은 0이됩니다. 따라서 over의 값들은 모두 0입니다.
: V(terminal) = 0
V0값을 통해 점화식을 사용하여 V1값을 각 state(cool, warm) 에서 계산해보겠습니다. 이렇게 V2,3,...계산을 해 나갑니다.
V2를 계산했으면 이제는 V1은 지워도 되고 이렇게 계속 반복해 올라갑니다. 이렇게 올라가다가 converge하면 그것이 V* 가 됩니다.
이 경우에는 converge하지 않지만 discounted vector를 1보다 작게 하면 conv합니다.
만약 action space가 크다면, 다른 말로 action의 개수가 너무 많다면 계산해야 할 양이 너무 많아집니다. 속도가 훨씬 느려집니다. 이렇게 action의 개수에 비례하여 계산량이 증가한다는 점이 단점입니다.
그리고 많은 MDP에서 V* 로 conv하기 위해서는 꽤 오래가야 합니다.
여기서 중요한 점은 현재 state이 warm이면 무조건 slow action이 좋고, 현재 sate이 cool이면 무조건 fast action이 좋습니다.
우리가 찾아야 할 것은 V 인 optimal state value ft값이 아니라, 각 state마다 어떤 action을 취하는 것이 더 좋은지 optimal policy를 찾는 것 입니다.
이 경우에서는 optimal state value ft V 을 찾기 이전에, optimal policy는 훨씬 이전 단계에서 알 수 있습니다!
value iteration은 중요한 세 단계가 있습니다.
1) value iteration 초기화
2) 점화식을 사용하여 converge할 때까지 가서 optimal state value ft V* 을 구하기
(대부분 여기서 시간을 소요
synchronous backup : 미리 state마다 계산해 놓고 동시에 update
asynchronous backup : 각각 따로 state마다 update(최근 update된 것을 사용 가능))
3) optimal state value ft값을 이용해서 optimal policy를 찾기
:optimal state value ft값을 통해 이를 이용해서 optimal action value ft을 만들고 maximize하는 방향으로 하여 optimal policy를 찾는 것 입니다. 여기서 위의 Vk+1 의 식과 유사하지만 최대값을 찾는 것이 아닌 최대를 만드는 각 action을 찾는 것 입니다. 방법은 동일하기에 one-step lookahead라고 합니다.
value iteration의 단점
1) 각 state마다 maximum을 취할 때, 위의 예시처럼 V 을 찾기 전에 maximize하는 action을 안다면 굳이 V 으로 converge시킬 필요가 없다.(필요 이상으로 계산을 많이 한 것)
2) 계산량이 너무 많습니다. 1 iteration은 Vk를 통해 Vk+1을 찾는 것인데 한 state에서 모든 action에 대해 계산을 하고, 이를 모든 state에서 반복해야 합니다. 또한 next state의 값을 이용해야 하기에 총 state개수^2* acoin개수인 per iteration O(AS^2) 가 됩니다.
이 두가지 단점을 보완해 만든 것이 policy iteration입니다.
아래는 value iteration의 수도코드입니다.
converge를 위한 입실론, arbitrarily initialized, V(terminal)=0
마지막으로 grid world에서의 테이블을 보겠습니다.
optimal policy를 구하는 방법은 optimal state value ft V 을 이용한 방법과 optimal action value ft Q 를 이용하는 방법이 있습니다. Q 를 이용한 방법이 더 쉽습니다.(이미 최적 action을 알고 있기에) 하지만 Q 를 계산하기 위해서 너무 많은 계산량이 요구됩니다.
V 는 s만큼 계산량이 요구된다면, Q 는 sxation 만큼 계산량이 요구됩니다.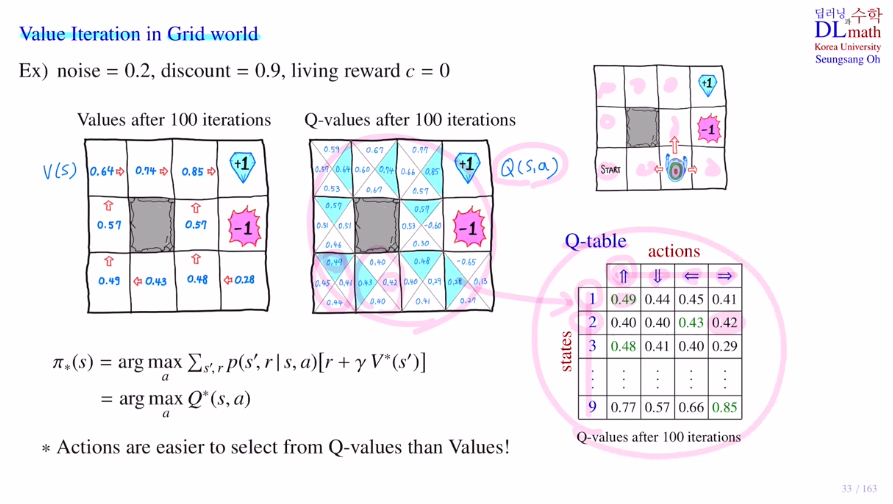
고려대학교 오승상 교수님 강화학습 강의 : https://www.youtube.com/watch?v=rC6xkxS_myY&list=PLvbUC2Zh5oJtYXow4jawpZJ2xBel6vGhC&index=8