퍼셉트론의 조합을 이용한 딥러닝
multi layer perceptron : 복잡한 문제를 해결할 수 있게 된다.
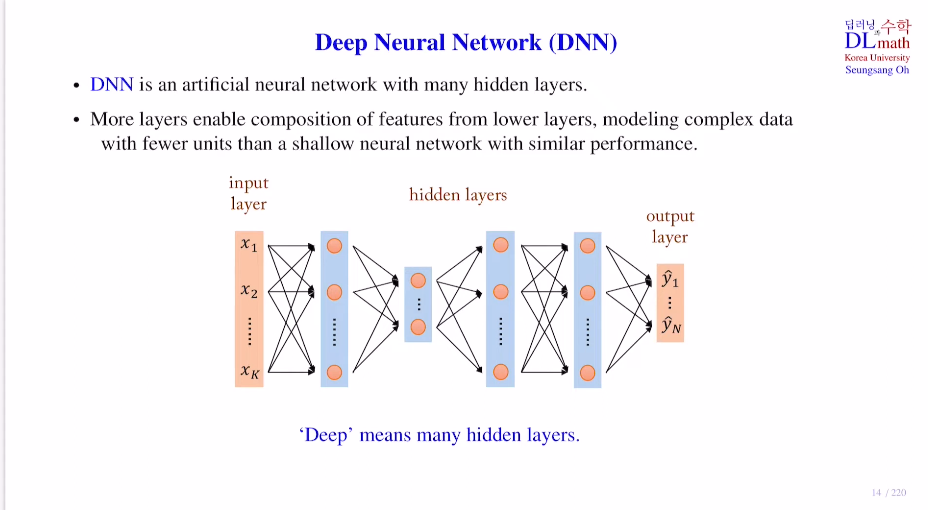
Deep Neural Network : DNN
: Input layer / Hidden layer / Output layer
weight sum + bias => activation ft => node:feature
이를 반복하며 깊은 hidden layer를 통과하고, 더욱 고도화된 추상적인 정보를 담는 feature 생성 => 이를 통해 최종적인 output layer 생성
++ 단순히 노드수만 늘려면 되는 것 아닌가? 이는 shallow network로 물론 이것도 성능이 괜찮게 나온다. 하지만! 노드 수가 동일하다고 가정했을 때, DNN의 성능이 더 우수하기에 DNN을 사용한다.
이유는 생각해보면 간단한데, DNN의 hidden layer가 깊어질 수록 최종 output layer의 노드에 도달하게 되는 경우의 수가 굉장히 많아지기 때문에 더욱 좋은 정보를 함축할 수 있기 때문이다.
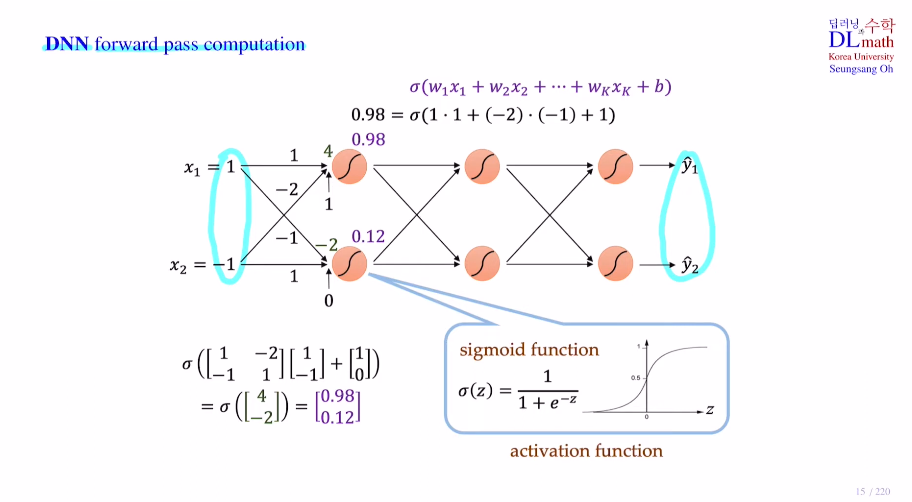
딥러닝 코드를 짜다보면 pytorch로 작성할 때, def forwar와 loss.backward() (backpropagation)를 작성하는데 여기서는 우선 forward pass에 대해 알아보자.
아래는 f:R2->R2 인데, 각 레이어마다 노드 2개씩 존재한다. 여기서 선형대수의 중요성이 나온다! weight sum을 진행할 때, weight가 많아질 수록 줄줄이 나열하여 식을 세우면 굉장히 명확하지 않다. 이를 행렬을 통해 간단히 표현할 수 있다. activation ft은 sigmoid로 주로 이진분류시 사용되는 활성화함수이다. 활성화함수는 conti&diff인데 이 이유는 차후 backpropagation을 진행해야 하기 때문이다. 물론 relu 와 leaky relu 등은 0에서 미분 불가하지만 자세한 내용은 backpropagation에서 다루겠다.
그렇다면 의문이 생길 수 있다. Q. 활성화함수는 왜 사용하는 것일까?
바로 non-linearlity때문이다! 활성화함수가 없다면(편향도 없다 가정) 결국 Wx(W=wL...w1)로 표현되는 것인데, 이는 단층 레이어와 다를 것이 없다. 그렇기에 activation ft을 통해 multi layer perceptron으로 깊게 쌓는 것이다!
강의에서 굉장히 좋은 예시를 들어주셨다. f = ax + b 라고 가정한다면 a3(a2(a1x+b1)+b2)+b3 = ax+b이다. 하지만 f = ax^2 + b라면?! 이는 ax^8+...로 8차식이 되는 것이다. 이렇게 고차원의 정보를 담을 수 있게 된다.

이제 Softmax에 대해 설명해보자. 이 함수는 output layer에서만 사용하게 된다.
sigmoid는 이진 분류에 주로 사용되었다면, softmax는 다중 분류에 사용된다.
idea : 시그모이드를 취하고 그에 따른 값을 도출하지 말고, 시그모이드 취하기 전 값을 바로 이용하자.
각 클래스의 확률은 아니지만 확률 값처럼 생각하여(최종합은 1) 가장 적합하다고 생각하는 하나를 선택하는 것이다. 이렇게 변경하면 사람이 이해하기 훨씬 쉬워진다. softmax로 output을 냈다면, np.argmax() or torch.max(output, 1) 로 하나를 선택한다. 그리고 loss ft을 이용하여 loss값을 구하고 backpropagatoin을 실행한다.
(중요한 점은 확률의 개념을 하나도 넣지 않았기에, 확률과 관련이 없지만 확률의 모습을 띄고 있다.)

고려대학교 오승상 교수님 딥러닝 : https://www.youtube.com/watch?v=bRp0HzlgMNU
