저번시간까지는 DNN과 forward pass computation을 배웠다면, 이제는 backpropagation을 위한 cost(loss) ft을 알아보자.
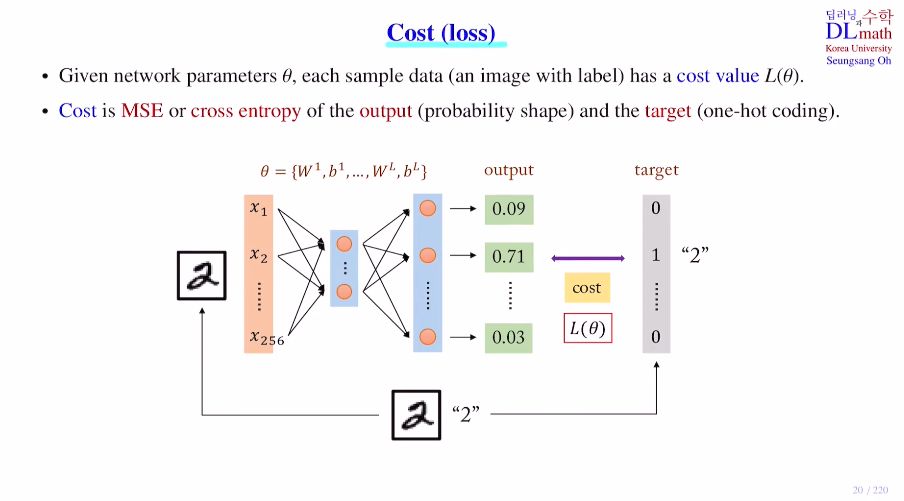
forward pass를 통해 도출된 output값을 이용하여 원래의 정답 라벨과 차이를 통해 cost value(L(θ))를 구한다.
(정답은 2일 때, 클래스 개수에 따라 원핫코딩으로 변환해주고, 이를 통해 cost값을 구한다.)
방법은 굉장히 많다. Categorical CrossEntropy, Sparse Categorical CrossEntropy, BinaryCrossEntropy, 회귀면 MSE, RMSE 등
데이터 하나만 가지고 성능이 좋은지 좋지 않은지를 따지기에는 무리가 있다. 그렇기에 Total Cost를 계산하게 되는데, 모든 training data에 대해 Total Cost C(θ)를 구하게 된다. 그리고 이를 이용하여 C를 minimize하는 방향으로 파라미터를 업데이트 해주는 것이다!
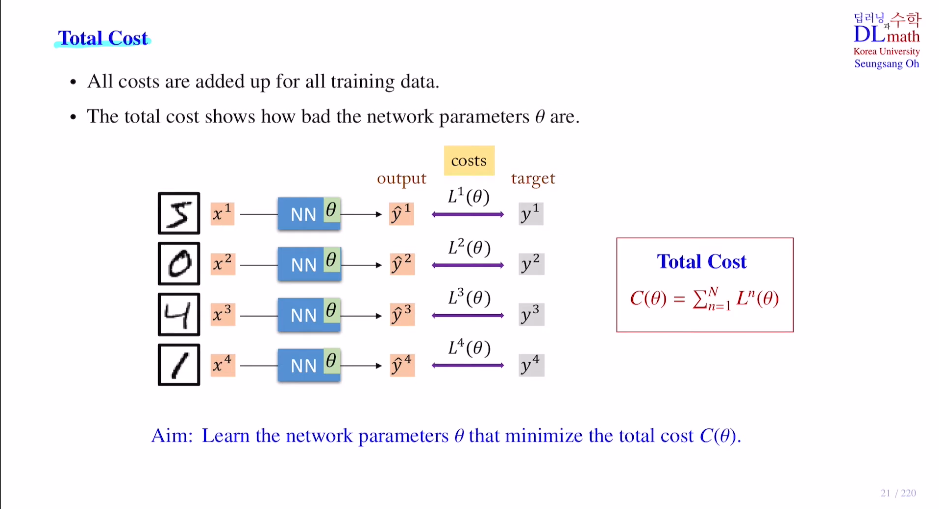
이렇게 Total Cost를 구했다면 Gradient Descent에 대해 알아보겠다.
목적은 Cost ft의 minimize인데, 이를 한번에 찾는 것이 아닌 조금씩 minimum으로 다가간다. iterative optimization algorithm
Gradient Descent Optimization Algorithms는 굉장히 많은데 이전에 작성했던
VAE 이해하기 위한 내용(1)
을 참고하면 이해가 수월할 것 같다.
각 변수에 대해 편미분을 통해 Gradient를 계산하고, 이 negative gradient방향을 이용하여 minimum으로 다가간다.
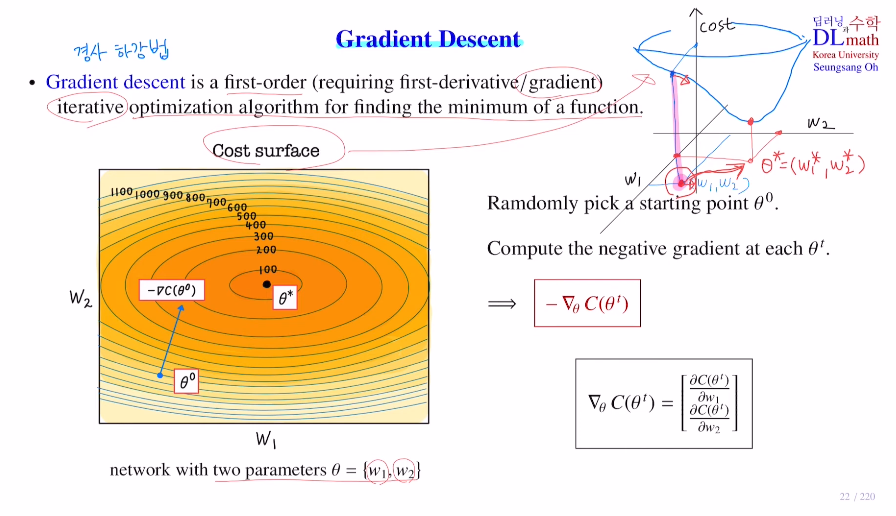
단순 미분으로 보면 이해하기 좋은데, 미분을 통해 기울기의 반대방향을 더해주어 minimum에 다가갈 수 있게 하는 것이다! 이렇게 조금씩 다가가며 파라미터를 업데이트 해준다.
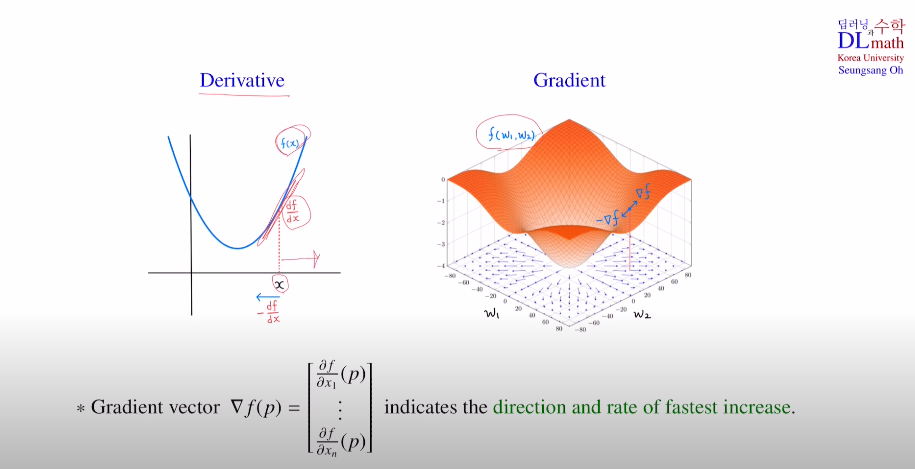
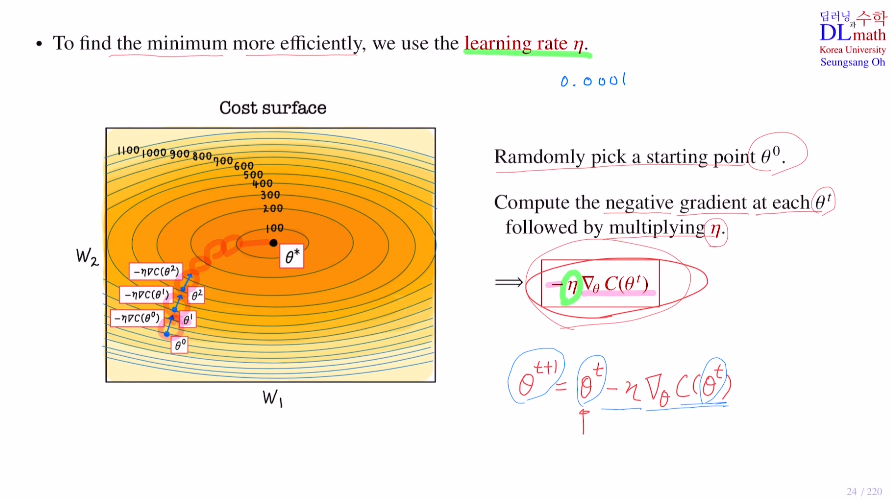
여기서 하나의 기법이 나온다. minimum에 다가가기 위한 효율적인 방법으로 learning rate (η)를 이용한다. 논문을 읽다보면 보통 0.001을 이용한다. 이렇게 조금씩 minimum으로 다가간다.
주의할 점은 이 learning rate를 잘 잡아야 하는데, local minimum에 빠질 위험이 있기 때문이다.
고려대학교 오승상 교수님 딥러닝: https://www.youtube.com/watch?v=bRp0HzlgMNU
