이번 포스터는 Wasserstein GAN : WGAN을 알아보자!
이 WGAN은 Wassestein distance를 이용한 cost ft을 활용하는 것이다.
우선 기존의 GAN은 학습할 때, non-convergence(minimax로 인해), mode collapse(한 가지 종류의 real data와 유사한 것을 만들었으면 이와 유사한 것만 만든다.), vanishing gradient problem(학습 초기에서는 판별자가 쉽게 구분하기에 gradient가 0에 가깝게 나오낟.)이 존재했다. 이 세 가지 문제로 인해 학습이 어려웠다.
이를 극복하기 위해 WGAN은 새로운 cost ft을 정의한다. 이때 사용하는 것이 Wassestein distance이다.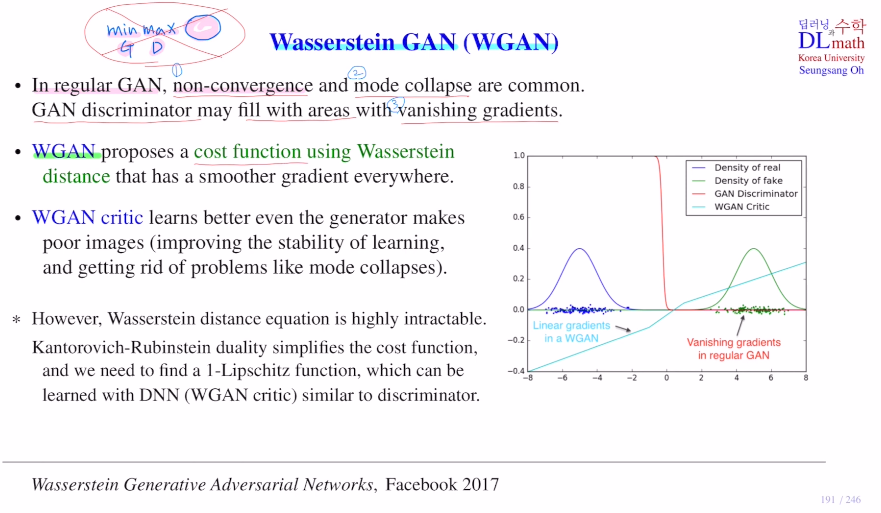
아래는 Distance와 divergence로 두 확률분포 사이의 거리를 확인하는 방법이다.
먼저 Distance(metric)을 알아보자.
확률분포 P,Q의 거리를 알고 싶은 것이다.
우선 거리 개념을 사용하기 위해 세 가지 조건이 있다.
1) d(P,Q)>=0 또한 d()=0 <=> P=Q almost everywhere ( :M({P!=Q})=0 )
2) d(P,Q) = d(Q,P) symmetriy
3) d(P,Q)<=d(P,R)+d(R,Q) triangle inequality
여기서 1)만 만족하는 조건을 divergence라고 한다. 이 diergence는 수학적으로 distance보다 약한 조건이긴 하지만 두 확률분포 사이의 거리 개념을 어느정도 줄 수 있기에 이것을 사용한다.
따라서 Wassestein distance를 알아보기 전, 자주 사용되는 divergence 세 가지를 알아보자.
1) Total Variation distance (1,2,3조건 모두 만족)
P(A)는 P라는 확률분포를 A라는 domain에서 적분한 것이다. 즉, 두 확률분포 사이의 면적의 sup을 구한 것이다. 이 델타 값을 점점 0으로 보내는 것이 좋은 것이다. 하지만 이것은 직관적으로 이해하기 쉽지만 sup을 다루기 어려워 잘 사용되지 않는다.
2) KL divergence (1만 만족)
p=q라면 값이 0이 된다. p가 더 크면 0보다 큰 값이 나오기에 파란 면적이 나온다. p가 더 작을 땐 음수값이 나오게 된다. 즉, 이 plog(p/q)를 그린 선을 적분한 값이 KD div값이 되는 것이다. 항상 0보다 큰 특징이 있지만, symetric하지 않기에 순서를 바꾸면 빨간색과 같은 그림이 나온다. 지금은 적분하면 같은 값이 나오는 것 처럼 보이지만 보통은 다른 값이 나온다. 또한 q=0이 되어 버리면 infinity값을 가질 수 있다는 단점이 있다. 그럼에도 다루기 쉽기에 딥러닝 및 강화학습에서 확률분포 사이의 거리를 측정하는데 잘 활용된다.
3) Jenson-Shannon divergence (1,2만 만족)
KL div를 약간 변형시킨 것으로 symmetric이며 infinity가 생기는 것을 막은 방법이다.
2),3)은 세 가지를 만족하지 않기에 metric은 아니다.
또한 disjoint supports를 갖게 되면 1)=1, 2)->무한대, 3)log2를 갖는다. 여기서 Q가 더욱 멀어져도 이와 같은 값을 갖는다. 즉, Q를 움직이게 하는 방법이 없다. 이 세 가지는 분포가 어느 정도 겹쳐있을 때만 사용이 가능하다. 이 문제를 Wassestein distance는 해결한다.
이제 Wassestein distance를 본격적으로 알아보자.
π(P,Q)를 set of all joint distribution γ(x,y)라고 할 때, 여기서 infimum을 구하는 것이다.
joint distribution을 아래와 같이 나타내고 이동시킬 때 이동량을 계산하면 왼쪽의 경우는 19(평균이기에 19/7), 오른쪽의 경우는 21(평균이기에 21/7)이 나온다. 그 이유는 왼쪽 경우는 모두 왼쪽에서 오른쪽으로 효율적으로 움직였지만, 오른쪽의 경우는 반대로 가는 것들이 있기에 비효율적으로 움직인다. 이런 여러 joint distribution이 있을 텐데 이 중 평균의 infimum을 찾는 것이다. 즉, 지금의 예에서는 왼쪽 것을 이용하는 것이다. 이렇게 optimal하게 이동하는 cost가 바로 Wassestein distance가 되는 것이다.
즉, 정리하자면 P라는 분포에서 Q라는 분포로 움직일 때 가장 효율적으로 움직이는 방법을 말한다.
: 분포 P에서 분포 Q로 optimal 하게 움직이는 cost
: P모래성을 Q모래성으로 움직인다고해서 Earth-mover distance라고도 한다.
두 번째 방법은 CDF라고 하는 cumulative distribution ft을 이용할 것이다.
P분포의 CDF라는 것은 x를 기준으로 왼쪽의 면적을 Fp(x)라고 한다.
누적 확률분포로 결국 증가함수로 총 1이된다.
P의 면적이 0.2에 해당하는 부분을 Q의 면적이 0.2에 해당하는 부분으로 이동시키는 것이다. 이렇게 비율을 맞추어 차근차근 움직인다.
CDF를 보면 P는 a점에서 0.2를 가졌고, Q는 b점에서 0.2를 갖는다. 이 P의 a점을 면적은 0.2로 유지하며 점점 b쪽으로 이동시키는 것이다. 즉, 총 P가 Q로 이동하는 이동향은 CDF의 면적이 될 것이다. 각각의 가로 길이들은 Fp의 역함수에서 Fq의 역함수를 뺀 것으로 생각할 수 있기에 이 거리들을 0~1까지 적분한 것이 아래의 식이 된다.
앞의 세 식은 분포의 위아래 차이를 비교하여 정의했지만, 이번에는 한 점을 오른쪽 한 점으로 이동시키는 것에 대해 정의한 것이다! 그렇기에 disjoint supports에 대해서도, Wassestein distance은 점을 움직이는 것이기에 이렇게 점점 멀어져도 값이 점점 커지게 할 수 있는 것이다!
따라서 이를 통해 GAN의 초반 학습시 발생하는 fake data의 분포와 real data의 분포의 차이가 클 때, 2,3과 달리 Wassestein distance는 gradietn descent 알고리즘으로 거리를 효과적으로 줄일 수 있게 되는 것이다!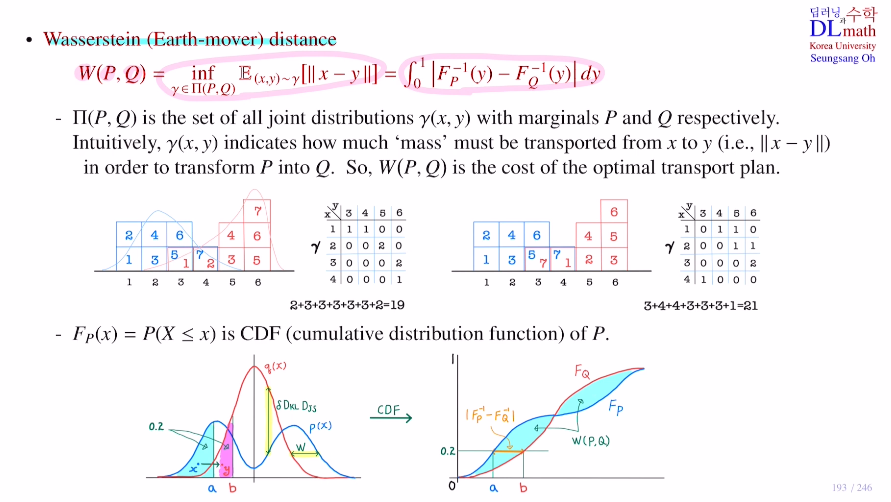
따라서 기존 GAN은 minimax로 풀었다면, WGAN은 Wassestein distance를 통해 cost ft을 정의하고, 이를 minimize시키는 쪽으로 학습을 진행하는 것이다.
이 cost ft을 정의하는 과정에서 판별자를 사용하지 않고, WGAN critic이라는 것을 사용한다. 아래 그림을 보면 real data 분포가 fake data분포가 많이 떨어져 있다. 학습 초기에는 생성자의 성능이 좋지 않기에 주로 이렇게 나온다. 이 경우 판별자는 real에서는 거의 다 1, fake data에서는 거의 다 0이기에 미분을 해도 0에 가까운 값만 내보내는 것이다. 따라서 vanishing gradient문제가 생긴다.
여기서 WGAN critic을 사용하면 linear 형태가 나오기에 gradient가 0이 나오지 않게 된다. 따라서 학습 초기에 생성자의 성능이 별로 좋지 않더라도 update를 잘 하여 성능을 잘 향상시킬 수 있게 된다. 또한 Wassestein distance를 정의해서 사용하기에 non-convergence문제도 어느정도 해결한다.
또 하나 더 언급할 점은 mode collapse 문제를 Wassestein distance는 점 자체를 이동시키기에 distance자체를 줄이므로 분포 자체가 비슷해져 골고루 이미지를 생성한다. 따라서 mode collapse 문제를 해결하게 된다.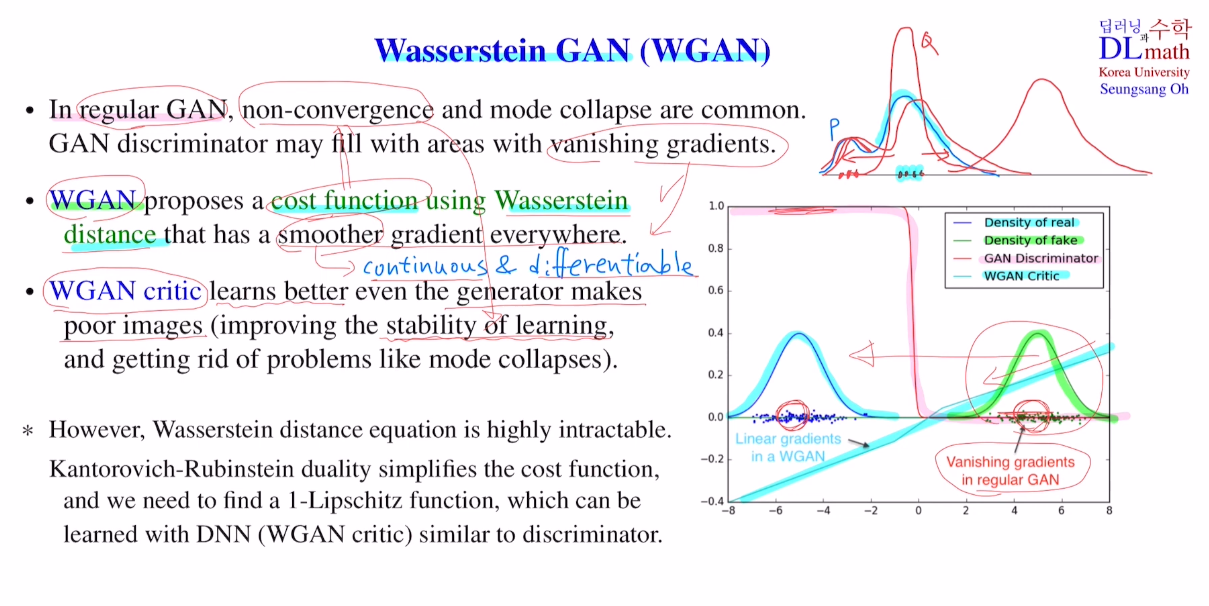
고려대학교 오승상 교수님 딥러닝 강의 : https://www.youtube.com/watch?v=Fsv57RcHRWQ&list=PLvbUC2Zh5oJvByu9KL82bswYT2IKf0K1M&index=43
