cost ft을 통해 weight와 bias를 업데이트 시키는데, 이 업데이트를 하는 과정에서 식이 굉장히 복잡하고 파라미터의 수가 많다면 계산하기 까다로울 것이다. 이를 방대한 계산량을 보완하기 위해 나온 것이 바로 backpropagation이다! 컴퓨터가 효율적으로 계산할 수 있게 한 것인데, forward pass와 달리 코스트에 있는 오차를 역으로 보내는 것이다.
single layer를 예로 들어보자.
forward pass : weight sum->activation ft
이렇게 나온 결과값을 이용하여 Cost를 구하고(아래는 MSE), Backpropagation을 진행한다.
여기서 의문이 생길 수 있다. MSE는 N으로 나누어야 하지 않나?
사실 Cost의 값은 중요하지 않다. 중요한 것은 Cost를 minimize하는 것!
Gradient방향은 바뀌지 않기에 1/N 이나 1/2를 해도 상관이 없는 것이다.
(추가로 1/2로 한 이유는 미분을 진행할 때 2가 곱해지기에 이렇게 설정한 것)
최적의 파라미터를 찾기 위해 계속 업데이트를 하는데, 아래와 같은 식을 통해 다음 weight를 반복적으로 찾게 된다. ∂C/∂wi 를 구하기 위해 Chain rule을 통해 순차적인 미분으로 backpropa를 수행한다. 이렇게 gradient를 손쉽게 계산할 수 있는 것이다!
(여기서는 n개의 data에 대해 Total Cost를 계산하기 때문에 n개를 sum해야 한다.)
정리하자면, layer가 깊어질 수록 합성함수가 연속됨에 따라 gradient를 계산하기에 굉장히 복잡해진다. 이를 chain rule로 따져보니 컴퓨터 메모리에 저장되어 있던 x,y의 값만으로 사칙연산만을 통해 바로 계산이 가능하다! 계산해야할 양은 많지만 계산 자체는 굉장히 쉽다. 그렇기에 많은 양의 파라미터가 존재할 때, Cost ft의 편미분을 진행하기 위한 효율적인 방법이 backpropagation인 것이다.
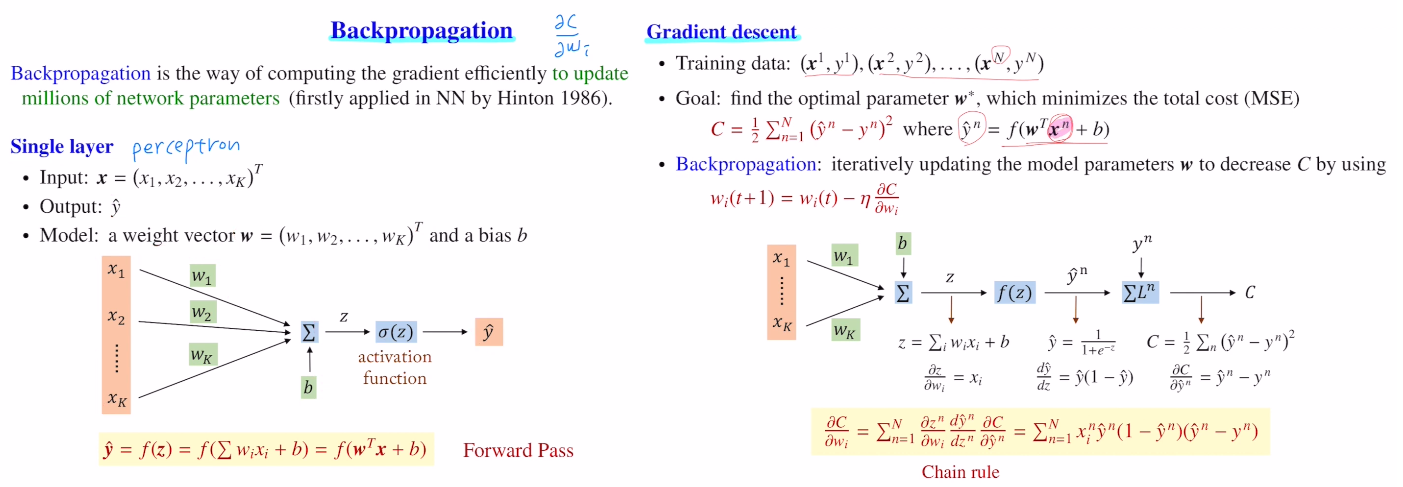
이번에는 Multi layer에 대해 살펴보자.
차이점이라고는 sumation의 개수가 달라진다. (k는 output의 dim이다.)
아래는 5번의 합성함수를 거치게 된다. 다시말해, Chain rule을 통해 5번의 편미분을 진행한 것이다.
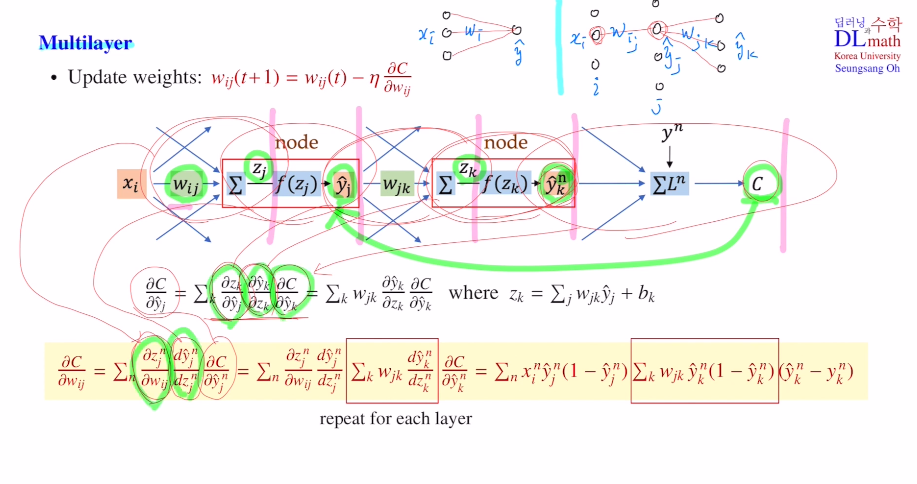
perceptron에서 계산했던 내용을 가져오면 식이 간단히 바뀐다!(y는 sigmoid미분한 것)
즉, 레이어가 늘어남에 따라 weighted sum을 미분한 값인 파라미터값과 activation ft을 미분한 값(이도 이미 저장되어 있는 output값)이 계속 추가되는 것이다.
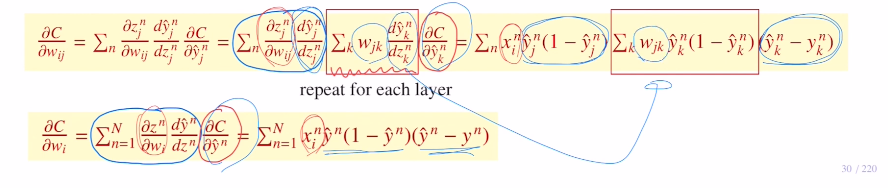
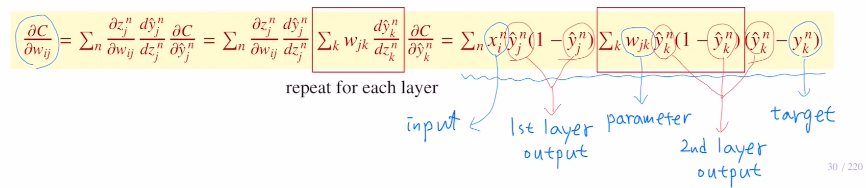
최종적으로 정리하면 아래와 같이 표현할 수 있게 되는 것이다!
이는 이미 forward pass를 진행할 때, 이미 계산했던 내용들로 컴퓨터 메모리에 저장되어 있는 값들이다. 즉, weight update시 gradient를 계산해야 하지만, 새로운 것을 추가적으로 계산하는 것이 아닌, forward pass를 이용할 때 주어졌던 값을 이용하여 사칙연산만으로도 gradient를 손쉽게 구할 수 있고 파라미터를 업데이트 할 수 있는 것이다.
고려대학교 오승상 교수님 딥러닝 : https://www.youtube.com/watch?v=2DYxY2T8y9Q&list=PLvbUC2Zh5oJvByu9KL82bswYT2IKf0K1M&index=6

