핸즈온 머신러닝
Part1. 머신러닝 ch5. 서포트 벡터 머신
- 선형 SVM 분류
- 비선형 SNM 분류
- SVM 회귀
- SVM 이론
SVM은 선형, 비선형 분류, 회귀, 이상치 탐지에 사용할 수 있는 다목적 머신러닝 모델입니다.
복잡한 분류 문제에 잘 들어 맞으며, 작거나 중간 사이즈의 dataset에 적합합니다.
1. 선형 SVM 분류
SVM의 support vector는 경계에 있는 샘플입니다.
SVM은 특성의 스케일에 민갑합니다. margin을 만들 때 거리에 의존하기에 스케일링을 통해 조정하여 결정 경계를 만들어 줍니다.
SVM에서 이상치가 존재할 경우 SVM은 거리를 따지기에 굉장히 좋지 않은 모델이 생성됩니다. 따라서 이런 경우 이상치를 제거 후 하드 마진 분류를 하거나, 일부는 무시하는 소프트 마진 분류를 실행합니다.
이 마진 사이즈는 하이퍼 파라미터 C를 통해 조절해주며, C값이 작아 마진이 넓을 수록 오류는 많을 수 있어도 일반화가 됩니다.
보통 SVM에서는 힌지 손실이 사용됩니다.
Word2Vec 2를 이해하기 위한 내용(4) - hinge loss : 힌지 손실
import numpy as np
from sklearn import datasets
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
iris = datasets.load_iris()
X = iris['data'][:, (2,3)] # 꽃잎의 너비, 길이
y = (iris['target']==2).astype(np.float64) # 아이리스 virginica인지, 아이리스 versicolor인지
svm_clf = Pipeline([
("scaler", StandardScaler()),
("linear_svc", LinearSVC(C=1, loss='hinge'))
])
svm_clf.fit(X, y)
---
svm_clf.predict([[5.5, 1.7]]) # 꽃잎의 너비, 길이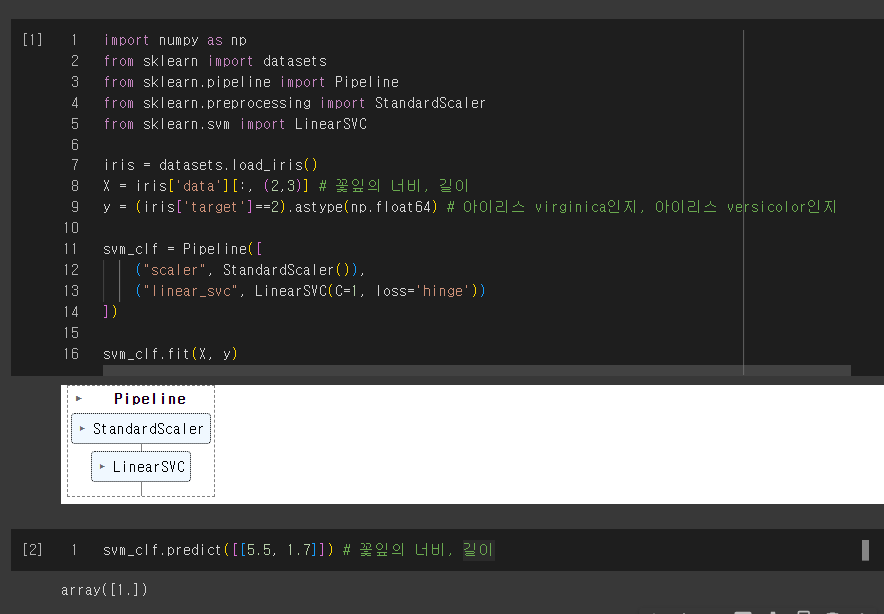
2. 비선형 SVM 분류
[ 방법1 ]
from sklearn.datastes import make_moons
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
X, y = make_moons(n_smaples=100 ,noise=0.15)
poly_svc = Pipeline([
('poly_features', PolynomialFeatures(degree=3)),
('scaler', StandardScaler()),
('svm_clf', LinearSVC(C=10, loss='hinge'))
])
poly_svc.fit(X, y)[방법2]
커널트릭을 사용하기
다항식 커널
from sklearn.svm import SVC
poly_svc = Pipeline([
('scaler', StandardScaler()),
('svm_clf', SVC(kernel='poly', degree=3, coef0=1, C=5))
])
poly_svc.fit(X. y)[방법3]
가우시안 RBF커널
유사도 함수를 이용하며, 감마가 증가할 수록 종 모양이 좁아짐을 의미합니다.
감마가 커질 수록 더욱 세세하게 나눌 수 있게 됩니다.
from sklearn.svm import SVC
poly_svc = Pipeline([
('scaler', StandardScaler()),
('svm_clf', SVC(kernel='rbf', gamma=5, C=0.001))
])
poly_svc.fit(X. y)
참고할 점은 LinearSVC가 SVC(kernel='linear') 보다 훨씬 빠르다는 점 입니다.
보통은 RBF kernel이 성능면에서 우수하지만 훈련 set이 크거나 특성 수가 많을 때 속도에서는 LinearSVC가 좋습니다.
3. SVM 회귀
회귀에서는 위에서 한 분류와는 반대로만 진행하면 됩니다.
이제는 마진 내에 최대한 많은 데이터가 들어오게 하면 되는 것 입니다. 이 마진의 폭은 입실론이라는 하이퍼파라미터를 통해 조절합니다.
여기서도 마찬가지로 LinearSVR와 SVR()를 통해 모델을 구축할 수 있고, 속도 또한 LinearSVR이 우수합니다.
from sklearn.svm import SVR, LinearSVR
# LinearSVR
linear_svr = Pipeline([
('scaler', StandardScaler()),
('linear_svr', LienarSVR(epsilon=1.5))
])
linear_svr.fit(X. y)
# SVR
svr_kernel = Pipeline([
('scaler', StandardScaler()),
('svr_kernel', SVR(kernel='poly', degree=2, C=100, epsilon=1))
])
svr_kernel.fit(X. y)4. SVM 이론
SVM의 목적은 결국 마진을 최대화하는 것 입니다.
그러한 초평면을 찾는 것인데, 3차원으로 생각해보면 결국 Decision ft이 최대한 누워서 마진을 기우게 학습을 진행하면 되는 것 입니다.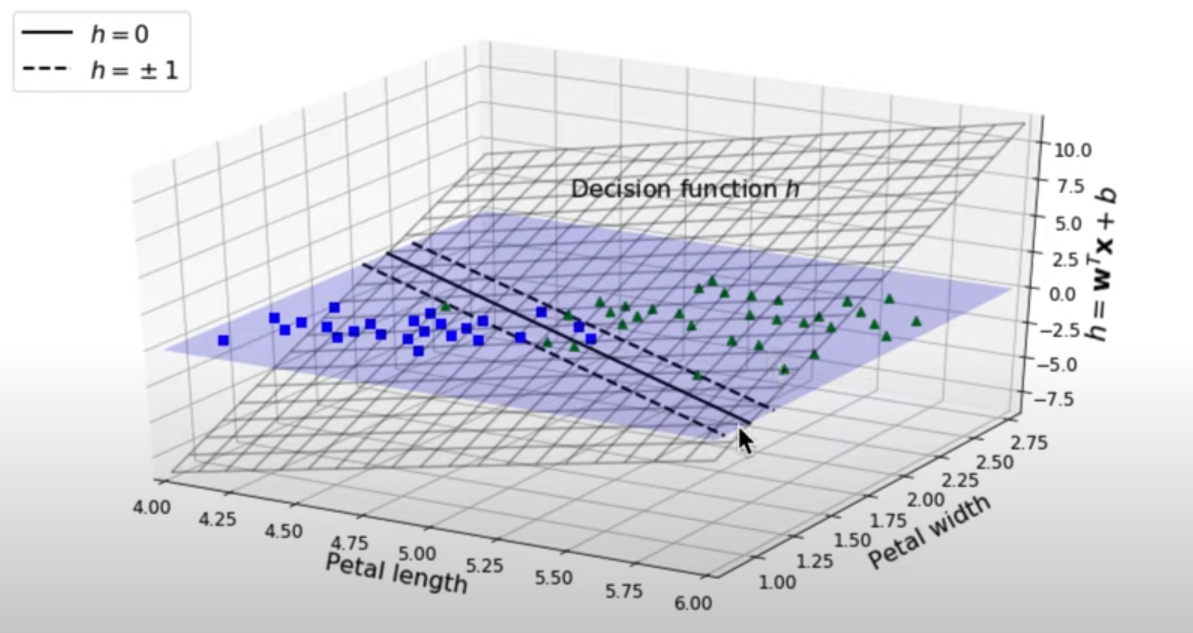
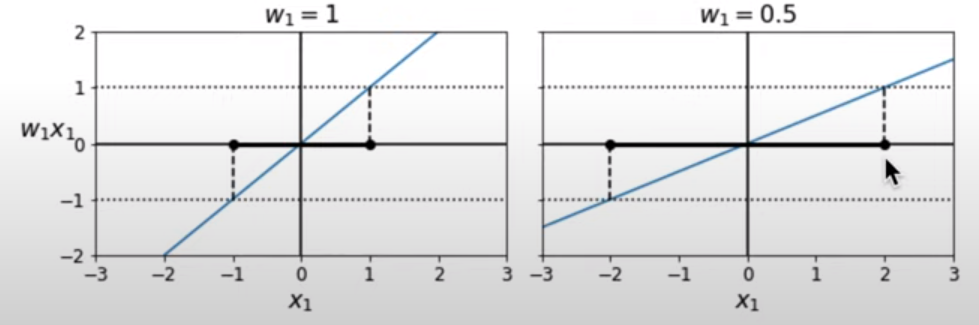
즉, 기울기를 나타내는 W의 norm을 최소화시키는 것이 목표가 됩니다.
(아래는 기울기에 따른 마진 예시 입니다.)
이 목표를 실행하기 위해 아래와 같은 식이 완성됩니다.
하드 마진의 경우 모든 데이터가 마진 안에 있으면 되지 않기에 힌지손실함수를 적용하면 모두 1보다 크거나 같아야 합니다!
소프트 마진의 경우는 슬랙변수를 첨가하여 샘플이 얼마나 마진을 위반해도 괜찮은지 설정해줍니다.

Kernel trick을 알아보자면 아래와 같이 굳이 2차 다항식을 통해 특성을 늘리지 않더라도, a와 b를 점곱을 통해 특성을 늘려서 곱한 것과 같은 효과를 발휘할 수 있습니다. 이렇게 두 벡터 사이의 거리를 마치 고차원 특성에서 거리를 계산한 것과 같은 효과를 볼 수 있습니다.