핸즈온 머신러닝

Part1. 머신러닝 ch4. 모델 훈련

• 선형회귀
• 경사하강법
• 규제가 있는 선형 모델

4.1 선형 회귀

선형 회귀의 cost ft이 MSE라고 할 때, 이 cost ft을 최소화 시키는 값은 무엇일까?
1) 미분을 통해 나온 정규방정식(normal equation) 풀기
2) 역행렬이 불가할 때, 유사역행렬(pseudoinverse) 찾기
3) 경사하강법

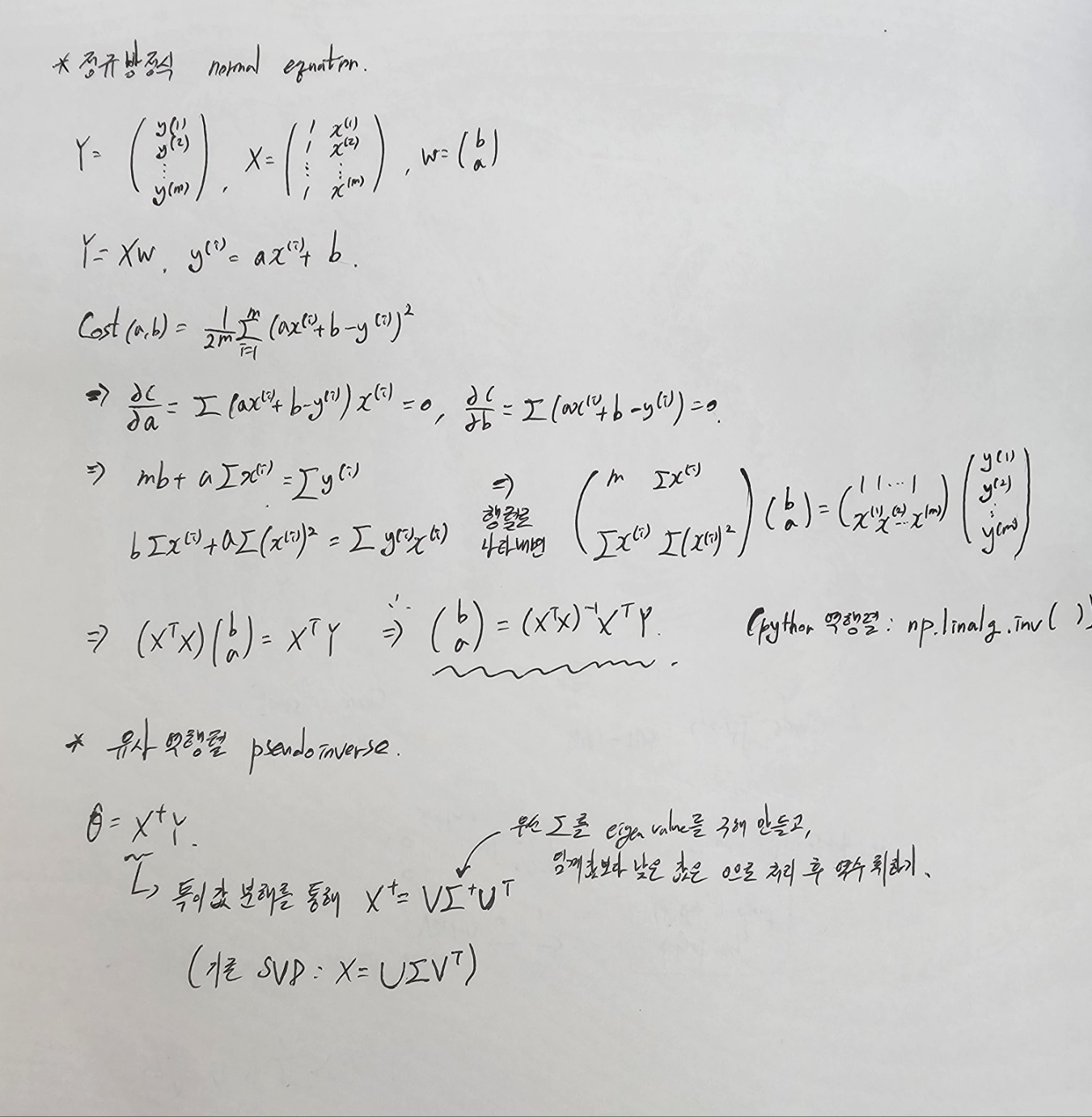
4.2 경사하강법

이전에 VAE논문을 보며 공부했던 내용인데 참고하면 좋을 것 같다.
VAE 이해하기 위한 내용(1) - Gradient Descent Optimization Algorithms

1) Batch Gradient Descent
2) Stochastic Gradient Descent
SGD를 사용할 때는 훈련 샘플이 IID(Independent and Identically Distribution)를 만족해야 평균적으로 파라미터가 global optimal을 향해 간다고 보장할 수 있다.
이를 위해 shuffle을 진행한다. 만약 그렇지 않을 경우 먼저 한 레이블에 대해 최적화하고, 그 다음 두 번째 레이블을 최적화하는 식으로 진행된다. 결국 이 모델은 최적점에 가깝게 도달하지 못 한다.

Q. 왜 IID를 따르지 않으면 최적점에 가깝게 도달하지 못 할까?
Local Minima에 갇힐 수 있음: 훈련 데이터가 IID를 만족하지 않으면, 모델은 특정 레이블 또는 패턴에 민감해질 수 있습니다. 이로 인해 모델은 지역 최소값(local minima)에 빠져서 전역 최소값(global minimum)으로 이동하지 못할 수 있습니다. 각 레이블을 순차적으로 최적화하면, 먼저 최적화된 레이블에 대한 편향된 가중치가 되어, 나중에 최적화해야 할 레이블에 영향을 미치는 것이 일반적입니다.

Gradient의 일관성 부족: IID를 만족하지 않으면 각 샘플 간의 상관관계가 높아질 수 있습니다. 이로 인해 그레디언트(gradient)가 불안정해지며, 최적화 과정이 불안정해질 수 있습니다. 이는 경사 하강법이 최적화 과정 중에 발산하거나 수렴하는데 어려움을 줄 수 있습니다.

Overfitting의 위험: 데이터가 IID를 만족하지 않으면 모델이 훈련 데이터에 과적합(overfitting)될 가능성이 증가합니다. 이는 모델이 훈련 데이터의 특정 패턴을 학습하고 일반화하기 어렵게 만들 수 있습니다.

수렴이 느려질 수 있음: IID를 만족하지 않는 데이터에서는 수렴이 더 느리게 일어날 수 있습니다. 이는 최적화 과정이 불안정하고 더 많은 반복이 필요하게 만듭니다.

3) Mini-batch Gradient Descent
미니배치로 나누어 학습을 진행

4.4 규제가 있는 모델

1) 릿지
2) 라쏘
3) 엘라스틱 넷