핸즈온 머신러닝

Part1. 머신러닝 ch9-2. 비지도 학습 - 가우시안 혼합

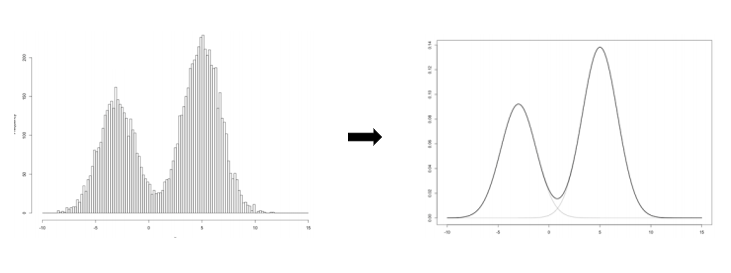
GMM은 전체 데이터를 몇 개의 가우시안 분포로 표현할 수 있다고 가정하여 각 분포에 속할 확률이 높은 데이터로 군집을 형성하는 기법입니다.

GMM은 기존 K-means, DBSCAN과 다르게 확률을 통해 군집을 형성합니다.

GMM의 파라미터 : 평균, 분산, 각 분포가 선택될 사전확률
전체 데이터를 표현할 K개의 가우시안 분포를 알아야 하며 그 분포의 모수(평균, 분산)이 필요합니다. 마지막으론 각 분포가 선택될 확률이 필요합니다.

우선 아래의 라벨이 있는 데이터의 경우 각각을 MLE를 통해 최적의 가우시안 분포를 찾아줄 수 있습니다.

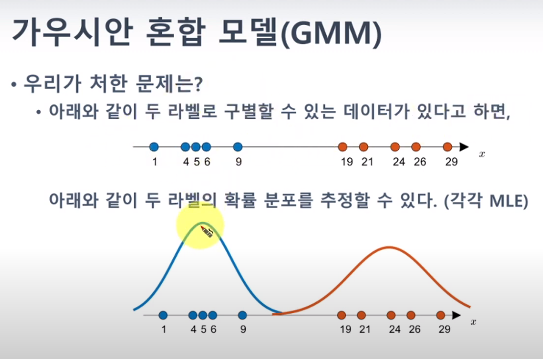
하지만! 만약 라벨이 없다면?!
라벨이 있으려면 분포가 있어야 하고, 분포를 얻으려면 라벨이 필요합니다.
따라서 라벨을 랜덤하게 주고 시작하거나 분포를 랜덤하게 설정해주는 둘 중 하나의 방법을 사용합니다.

가우시안 혼합 모델에서는 보통 분포를 랜덤하게 설정해주고 시작합니다.
두 개의 분포가 있을 것이라 상정하고(k-means와 같은 하이퍼 파라미터), 각 분포에 대한 모수를 랜덤하게 선정합니다. 이렇게 되면 하나의 데이터에 대해 각 분포의 우도값 중 더 큰 곳에 클래스를 할당할 수 있습니다.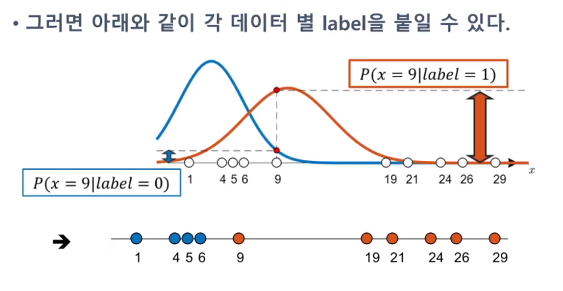

이렇게 얻어낸 라벨을 이용해서 각 그룹의 모수를 다시 추정해줍니다. 이렇게 라벨을 주고 우도를 추정하고, 를 반복하며 원하는 분포를 만들어냅니다.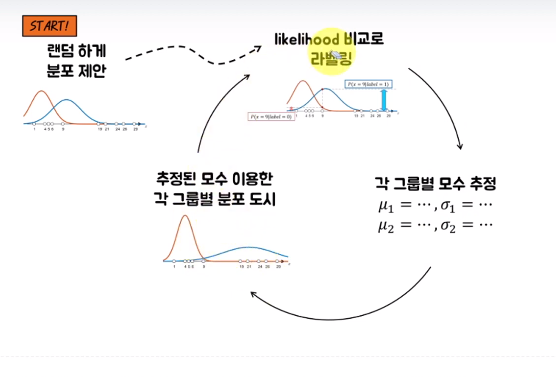

이제는 GMM을 수식으로 한 번 설명해보겠습니다.

EM:Expectation-Maximization 알고리즘을 기반으로 하고 있습니다.
EM알고리즘은 위에서 설명한
Expectation : 각 데이터에 라벨을 부여하는 과정
Maximization : 각 그룹의 모수를 재 계산하는 과정
입니다

wj(i) : i번째 데이터가 j번째 그룹에 들어갈 확률 입니다.
평균과 시그마는 분포를 우선적으로 가정했기에 알고 있는 값이고, 파이는 각 label별 weight의 합 입니다.

이 확률값을 통해 데이터의 그룹을 지정해주게 됩니다.(라벨링)

위 식을 베이즈정리를 통해 풀어주면 (likelihood)(prior) / (evidence) 가 됩니다.
likelihood : 분포를 가지고 높이 값
prior : 모든 데이터를 통틀어 1번 그룹에 있을 확률과 2번 그룹에 있을 확률
evidence : 모든 가능한 그룹에 대해 (likelihood)x(prior) 를 전부 더해 놓은 것
evidence는 전체를 확률로 만들기 위해 정규화 시키는 것

위의 내용이 E-step이고, M-step에서는 최대우도법을 이용해 모수를 계산해주면 됩니다.(여기서는 평균, 표준편차만 계산해주면 끝!)
추가적인 모수 파이는 각 그룹에 속할 평균확률입니다.(처음에는 0.5 0.5로 초기화되어 있습니다.)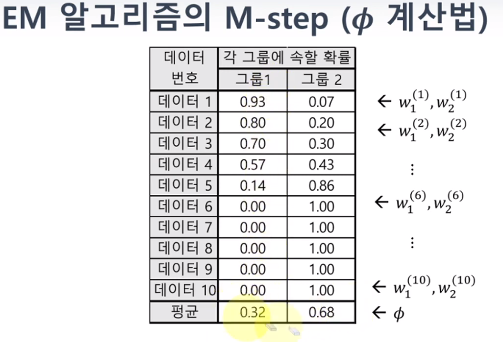

이렇게 라벨 구하고 모수 추정함을 반복하며 수렴시킵니다.

위의 내용은 https://www.youtube.com/watch?v=NNwkDi-2xVQ 을 참고하였습니다.

여기서의 우선 포인트는 "라벨이 주어져 있지 않다"는 것입니다.

GMM은 EM 알고리즘의 하위 분류라고 생각하면 됩니다. 그러니까, 데이터의 라벨이 주어져있지 않을 때 데이터가 분포한 형태만을 가지고 확률 분포를 fitting하는 알고리즘을 EM 알고리즘이라고 생각한다면, GMM은 확률 분포가 가우시안 분포로 선택한 경우라고 할 수 있습니다.

EM알고리즘은 local maximum에 빠질 위험이 있기에 조심해야 합니다.

이 가우시안 혼합모델의 코드는 간단합니다.

from sklearn.mixture import GaussianMixture

gm = GaussianMixture(n_components=3, n_init=10, random_state=42)
gm.fit(X)

---

gm.weights_
gm.means_
gm.covariances_

---

gm.converged_
gm.n_iter_

---

gm.predict(X)
gm.predict_proba(X)

가우시안 혼합 모델은 생성 모델 입니다!
즉, 이 모델에서 새로운 샘플을 만들 수 있는 것 입니다.

X_new, y_new = gm.sample(6)

또한 주어진 위치에서 모델의 밀도 또한 추정할 수 있습니다.

gm.score_samples(X)
# 이 점수의 지숫값을 계산하면 샘플의 위치에서 PDF값을 얻을 수 있습니다.(이 값은 하나의 확률이 아니라 확률 밀도입니다. 즉 1보다 작은 것이 아닌 어떠한 값도 될 수 있습니다.)

이 가우시안 혼합 모델은 특성이나 클러스터가 너무 많거나 샘플이 적을 때는 EM이 최적의 솔루션으로 수렴하기 어렵습니다. 따라서 클러스터의 모양과 방향의 범위를 제한할 수 있습니다. 공분산 행렬에 제약을 추가하는 방법인 covariance_type 매개변수에
spherical : 모든 클러스터가 원형
diag : 클러스터 크기와 모양에 상관없지만 타원의 축은 좌표축과 나란해야 합니다.(즉 공분산 행렬이 대각행렬이어야 합니다.)
tied : 모든 클러스터가 동일한 타원 모양, 크기, 방향을 가집니다.(즉 모든 클러스터는 동일한 공분산 행렬을 공유합니다.)

1. 가우시안 혼합을 사용한 이상치 탐지

가우시안 혼합 모델을 이상치 탐지에 사용하는 방법은 밀도가 낮은 지역에 있는 샘플들을 이상치로 보는 것 입니다. 밀도 임계값을 설정하여 이보다 낮은 곳에 있는 데이터는 이상치로 판단하는 것 입니다.

아래는 4%를 밀도 임계값으로 두어 이상치를 구분하는 코드입니다.

densities = gm.score_samples(X)
density_threshold = np.percentile(densities, 4)
anomalies = X[densities < density_threshold]

이렇게 이상치를 제거하여 정제된 데이터셋에서 모델을 훈련합니다.

이와 비슷하게 특이치 탐지가 있습니다. 이 알고리즘은 이상치로 오염되지 않은 깨끗한 데이터셋에서 훈련한다는 것이 특징입니다.

k-means에서는 이너셔나 실루엣 점수를 통해 적절한 클러스터의 개수를 선정합니다.
하지만 이 방법은 클러스터가 원형이고 크기가 비슷할 때 주로 사용하는 방법이기에 타원형이나 크기가 다를 때는 안정적이지 않습니다.
가우시안 혼합은 따라서 BIC or AIC를 사용합니다.

BIC=log(m)p−2log(L^)

AIC=2p−2log(L^)

m 은 샘플의 개수입니다.
p 는 모델이 학습할 파라미터 개수입니다.
L^ 은 모델의 가능도 함수의 최댓값입니다. 이는 모델과 최적의 파라미터가 주어졌을 때 관측 데이터 X 의 조건부 확률입니다.
BIC와 AIC 모두 모델이 많은 파라미터(예를 들면 많은 클러스터)를 학습하지 못하도록 제한합니다. 그리고 데이터에 잘 맞는 모델(즉, 관측 데이터에 가능도가 높은 모델)에 보상을 줍니다.

gm.bic(X)
gm.aic(X)

2. 베이즈 가우시안 혼합 모델

최적의 클러스터 개수를 수동으로 찾지 않고 불필요한 클러스터의 가중치를 0으로 만드는 베이지안 가우시안 혼합 모델을 사용할 수 있습니다.

코드는 아래와 같은데 n_components는 최적의 클러스터 개수보다 크다고 믿을 만한 값으로 지정합니다.

from sklearn.mixture import BayesianGaussianMixture
bgm = BayesianGaussianMixture(n_components=10, n_init=10)
bgm.fit(X)
np.round(bgm.weights_, 2)

지금의 예시에서는 3개의 클러스터가 필요하다고 판단했습니다.

Scikit-learn의 BGMM (Bayesian Gaussian Mixture Model)은 가우시안 혼합 모델 (GMM)의 확장된 버전으로, 데이터를 잠재적으로 다른 클러스터로 그룹화할 수 있는 모델입니다. BGMM은 확장 가능한 모수 추정 방법을 사용하여 GMM의 클러스터 개수를 자동으로 선택하는 데 도움을 줍니다. 이를 위해 BGMM은 Variational Bayesian Inference을 사용합니다.

BGMM (Bayesian Gaussian Mixture Model) 설명:

1) 데이터 준비:
데이터를 수집하고 전처리합니다.

2) BGMM 모델 초기화:
BGMM 모델을 초기화합니다. 이 과정에서는 클러스터의 개수를 정하지 않습니다.

3) E-step (Expectation Step):
현재 모델의 파라미터를 사용하여 데이터 포인트가 어떤 클러스터에 속할 확률을 추정합니다.
이 확률은 가우시안 분포의 확률밀도함수로 계산됩니다.

4) M-step (Maximization Step):
클러스터 파라미터를 업데이트합니다.

이 단계에서 BGMM은 Bayesian 방법을 사용하여 클러스터의 개수를 자동으로 선택합니다.

BGMM은 Variational Bayesian Inference을 사용하여 사후 분포를 추정하고, 클러스터 파라미터를 최적화합니다.

BGMM의 중요한 차이점 중 하나는 클러스터의 개수를 자동으로 선택하는 데 있습니다. GMM은 클러스터 개수를 사용자가 직접 지정해야 합니다.

수렴 여부 확인:

수렴 조건이 충족될 때까지 E-step과 M-step을 반복합니다.

결과 분석:

수렴한 모델을 사용하여 데이터를 클러스터링하고, 클러스터 간의 관계를 분석합니다.
수식적으로, BGMM은 GMM의 확장된 형태입니다.

BGMM과 GMM의 주요 차이점:

클러스터 개수 선택: GMM에서는 사용자가 클러스터의 개수를 사전에 지정해야 합니다. 반면, BGMM은 클러스터 개수를 자동으로 선택합니다.

1) Variational Bayesian Inference 사용: BGMM은 Variational Bayesian Inference를 사용하여 모델을 학습하고 클러스터 파라미터를 추정합니다. 이를 통해 불필요한 클러스터가 제거되고 모델의 일반화 능력이 향상됩니다.

2) 확률적 모델 선택: BGMM은 다양한 클러스터 개수에 대한 확률적 모델을 제공하므로 모델 선택의 불확실성을 고려할 수 있습니다.

3) BGMM은 GMM보다 더 자동화된 방식으로 클러스터링을 수행하며, 클러스터 개수 선택 및 모델의 정규화에 대한 더 나은 접근 방식을 제공합니다.

베이즈 정리 P(z|X) = P(X|z)p(z)/p(X) 에서 분모 evidence P(X)는 가능한 모든 z값에 대해 적분해야 하기에 계산이 어렵습니다. 따라서 이를 해결하기 위해 변분 추론(variational inference) 이 있습니다. 이 방식은 variational parameter 람다를 가진 분포 패밀리 q(z;람다)를 선택합니다. 그 다음 q(z)가 p(z|X)의 좋은 근삿값이 되도록 이 파라미터를 최적화합니다.
q(z)에서 p(z|X)로의 KL발산을 최소화하는 람다값을 찾아 이를 해결합니다.
이 식은 증거의 로그(log(P(X)))에서 증거 하한(ELBO: evidence lower bound)을 뺀 식으로 다시 쓸 수 있습니다. 증거의 로그는 q에 의존하지 않기에 상수항이므로 KL발산을 최소화하려면 ELBO를 최대화해야 합니다.

ELBO를 최대화 하는 방법은 블랙박스 확률적 변분 추론:black box stochastic variational inference BBSVI 입니다.
이는 각 반복에서 몇 개의 샘플을 q에서 뽑아 변분 파라미터 람다에 대한 ELBO의 gradient를 추정하는 데 사용합니다. 그 다음 경사 상승법 스텝에서 사용합니다.
이 방법은(미분 가능하다면) 어떤 종류의 모델과도 베이즈 추론을 사용할 수 있게 만듭니다. 심지어 심층 신경망도 가능합니다.

: 이 심층 신경망에서 사용하는 베이즈 추론을 베이즈 딥러닝 basyesian deep learning이라고 합니다.

가우시안 혼합 모델은 타원형 클러스터에 잘 작동합니다. 하지만 다른 모양을 가진 데이터셋에서는 좋지 않은 결과를 얻게 됩니다. 예를 들어 초승달 모양의 군집은 타원형을 어떻게든 나누어 잡아버립니다. 하지만 밀도 추정은 잘 하기에 이런 경우에는 이상치 탐지로 사용할 수 있을 것 입니다.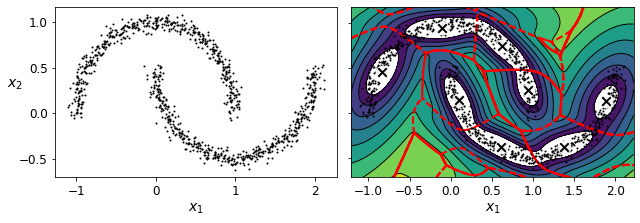

3. 이상치 탐지와 특이치 탐지를 위한 다른 알고리즘

1) PCA(그리고 inverse transform()메소드를 가진 다른 차원 축소 기법)

2) Fast-MCD(minimum covariance determinant)
이는 특히 데이터를 정제할 때 사용됩니다. 보통(정상) 샘플들이 혼합이 아닌 하나의 가우시안 분포에서 생성되었다고 가정합니다.

3) 아이솔레이션 포레스트
랜덤포레스트를 만들고 각 노드에서 특성을 랜덤하게 선택한 후 랜덤한 임곗값을 골라 데이터셋을 둘로 나눕니다. 이상치는 보통 다른 샘플과 멀리 있기에 평균적으로 정상 샘플과 적은 단계에서 격리 됩니다.

4) LOF (local outlier factor)
주어진 샘플 주위의 밀도와 이웃 주위의 밀도를 비교합니다. 이상치는 보통 KNN이웃보다 더 격리됩니다.

5) one-class SVM
여기서는 샘플 클래스가 하나이기에 one-class SVM으로 원본 공간으로부터 고차원 공간에 있는 샘플을 분리합니다.