핸즈온 머신러닝
Part1. 머신러닝 ch9-1. 비지도 학습 - 군집
8장에서는 가장 널리 사용되는 비지도 학습 방법인 차원 축소를 알아보았습니다.
이번 장에서는 추가적인 비지도 학습과 알고리즘을 알아보겠습니다.
- 군집
비슷한 샘플을 클러스로 모읍니다. - 이상치 탐지
정상 데이터가 어떻게 보이는지를 학습하고, 그 다음 비정상 샘플을 감지하는 데 사용합니다. - 밀도 추정
데이터셋 생성 확률 과정(random process)의 확률 밀도 함수(PDF)를 추정합니다. 이 밀도 추정은 이상치 탐지에 널리 사용됩니다. 밀도가 매우 낮은 영역에 놓인 샘플은 이상치일 간으성이 높습니다.
1. 군집
군집은 클러스터를 통해 그룹핑을 진행하는 것 입니다.
군집은 고객분류, 데이터 분석, 차원 축소, 이상치 탐지, 준지도 학습, 검색 엔진, 이미지 분할에서 사용됩니다.
1) K-means
군집 개수 k를 정해주면 그에 맞게 그룹핑을 해줍니다.
from sklearn.cluster import KMeans
k = 5
kmean = KMeans(n_clusters=k)
y_pred = kmeans.fit_predict(X)
---
# 5개의 센트로이드가 생성되었습니다.
kmeans.cluster_centers_Kmeans 알고리즘은 클러스터의 크기가 많이 다르면 잘 작동하지 않습니다.
하드 군집 : 결정경계를 그린 후 하나의 샘플이 들어오면 그에 맞게 분류
소프트 군집 : 모든 군집의 센트로이드 까지의 거리를 계산하여 어느 군집에 들어갈 지 분류
군집을 형성하는 방법
센트로이드 랜덤 설정 -> 샘플이 들어오며 평균을 통해 센트로이드를 업데이트
일반적으로 k-평균이 가장 빠른 군집 알고리즘 중에 하나입니다.
하지만 초기화할 때, 센트로이드의 위치를 군집에 근사하게 설정해 두면 훨씬 수월해 집니다. 따라서 1)센트로이드 리스트를 담은 넘파이 배열을 지정한 후 초기값으로 사용하거나 2) 랜덤 초기화를 여러번 한 후 가장 좋은 것을 뽑습니다. 이에 대한 성능 지표는 이너셔인데, 이것은 각 샘플과 가장 가까운 센트로이드 사이의 제곱 거리 합입니다.
good_init = np.array([[-3, 3],[-3,2],[-3,1],[-1,2],[0,2]])
kmeans = KMeans(n_clusters=5, init=good_init, n_init=1)
kmeans.fit_predict(X)
kmeans.inertia_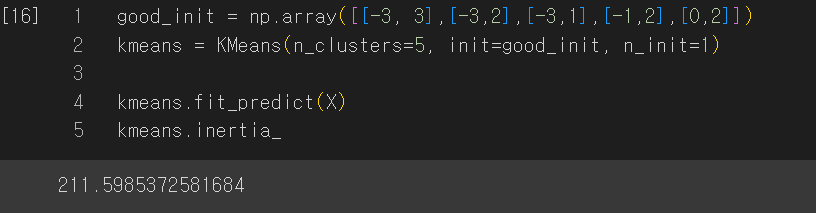
# 기본적으로 큰 값이 좋은 것이다 라는 규칙에 의해 : -무한대 ~ 0
kmeans.score(X)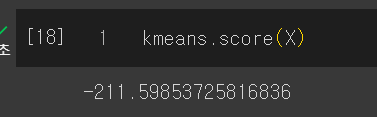
하지만 2006년에 k-평균++ 알고리즘이 나오며 반복 횟수를 줄이고 똑똑한 초기화를 할 수 있게 되었습니다.
센트로이드를 완전히 랜덤하게 초기화하는 대신 David Arthur와 Sergei Vassilvitskii가 2006년 논문에서 제안한 다음 알고리즘을 사용해 초기화하는 것이 더 좋습니다:
1) 데이터셋에서 무작위로 균등하게 하나의 센트로이드 c1 을 선택합니다.
2) D(xi)2 / ∑j=1mD(xj)2 의 확률로 샘플 xi 를 새로운 센트로이드 ci 로 선택합니다. 여기에서 D(xi) 는 샘플 xi 에서 이미 선택된 가장 가까운 센트로이드까지 거리입니다. 이 확률 분포는 이미 선택한 센트로이드에서 멀리 떨어진 샘플을 센트로이드로 선택할 가능성을 높입니다.
3) k 개의 센트로이드를 선택할 때까지 이전 단계를 반복합니다.
< 설명 2
1) (일단 아무 공간에나 중심점을 k개 찍고 시작하는 게 아니라) 가지고 있는 데이터 포인트 중에서 무작위로 1개를 선택하여 그 녀석을 첫번째 중심점으로 지정한다.
2) 나머지 데이터 포인트들에 대해 그 첫번째 중심점까지의 거리를 계산한다.
두번째 중심점은 각 점들로부터 거리비례 확률에 따라 선택한다. (뭔 소리야?) 즉, 이미 지정된 중심점으로부터 최대한 먼 곳에 배치된 데이터포인트를 그 다음 중심점으로 지정한다는 뜻이다.
3) 중심점이 k개가 될 때까지 2, 3번을 반복한다.
이 방법이 현재 default로 지정되어 있는 방법이며 가장 좋은 방법입니다.
1-1) 미니배치 k-평균
전체 데이터셋을 사용해 반복하지 않고 각 반복마다 미니배치를 통해 센트로이드를 조금씩 이동합니다. 속도를 높일 수 있다는 장점이 존재합니다. 하지만 이니셔는 일반적으로 조금 더 나쁩니다.(특히 클러스터의 개수를 증가할 때)
from sklearn.cluster import MiniBatchKMeans
minibatch_kmeans = MiniBatchKMeans(n_clusters=5)
minibatch_kmeans.fit(X)1-2) 최적의 클러스터 개수 찾기
그렇다면 클러스터의 개수는 어떻게 찾을까요?
우선 이너셔 그래프를 보며 꺾이는 엘보 부분을 선택할 수 있습니다.(이너셔는 계속 낮아지지만 적당한 군집은 엘보 부분)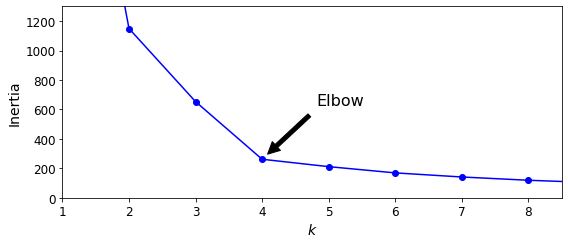
하지만 이 방법은 너무 엉성하기에 실루엣 점수(실루엣 계수의 평균)를 통해 측정합니다.
샘플의 실루엣 점수는 (b-a)/max(a, b) 이며, a는 동일한 클러스터에 있는 다른 샘플까지 평균 거리(즉 클러스터 내부의 평균 거리), b는 자신이 속한 클러스터 이외 가장 가까운 클러스터까지 평균 거리입니다. 이 값은 -1 ~ +1 로 1에 가까울 수록 자신이 속한 클러스터 안에 잘 속해있음을 의미합니다.
: a가 작아지고 b가 커질 수록 good
from sklearn.metrics import silhouette_score
silhouette_score(X, kmeans.labels_)
---
kmeans_per_k = [KMeans(n_clusters=k, random_state=42).fit(X)
for k in range(1, 10)]
silhouette_scores = [silhouette_score(X, model.labels_)
for model in kmeans_per_k[1:]]
plt.figure(figsize=(8, 3))
plt.plot(range(2, 10), silhouette_scores, "bo-")
plt.xlabel("$k$", fontsize=14)
plt.ylabel("Silhouette score", fontsize=14)
plt.axis([1.8, 9.5, 0.55, 0.7])
plt.show()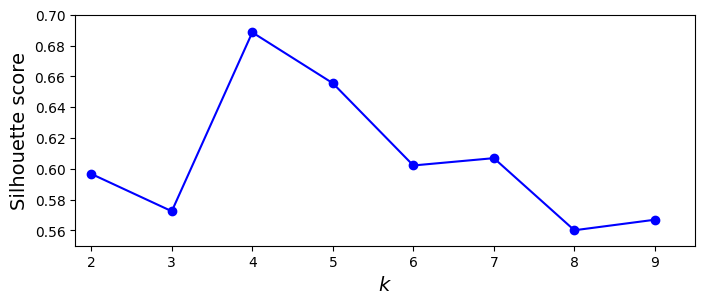
이렇게 이니셔를 비교했을 때 드러나지 않은 부분도 확인할 수 있음을 알 수 있습니다.
++ 모든 샘플의 실루엣 계수를 할당된 클러스터와 실루엣 값으로 정렬하여 그리면 훨씬 많은 정보를 얻을 수 있습니다. 이를 실루엣 다이어그램 이라고 합니다:
from sklearn.metrics import silhouette_samples
from matplotlib.ticker import FixedLocator, FixedFormatter
plt.figure(figsize=(11, 9))
for k in (3, 4, 5, 6):
plt.subplot(2, 2, k - 2)
y_pred = kmeans_per_k[k - 1].labels_
silhouette_coefficients = silhouette_samples(X, y_pred)
padding = len(X) // 30
pos = padding
ticks = []
for i in range(k):
coeffs = silhouette_coefficients[y_pred == i]
coeffs.sort()
color = mpl.cm.Spectral(i / k)
plt.fill_betweenx(np.arange(pos, pos + len(coeffs)), 0, coeffs,
facecolor=color, edgecolor=color, alpha=0.7)
ticks.append(pos + len(coeffs) // 2)
pos += len(coeffs) + padding
plt.gca().yaxis.set_major_locator(FixedLocator(ticks))
plt.gca().yaxis.set_major_formatter(FixedFormatter(range(k)))
if k in (3, 5):
plt.ylabel("Cluster")
if k in (5, 6):
plt.gca().set_xticks([-0.1, 0, 0.2, 0.4, 0.6, 0.8, 1])
plt.xlabel("Silhouette Coefficient")
else:
plt.tick_params(labelbottom=False)
plt.axvline(x=silhouette_scores[k - 2], color="red", linestyle="--")
plt.title("$k={}$".format(k), fontsize=16)
save_fig("silhouette_analysis_plot")
plt.show()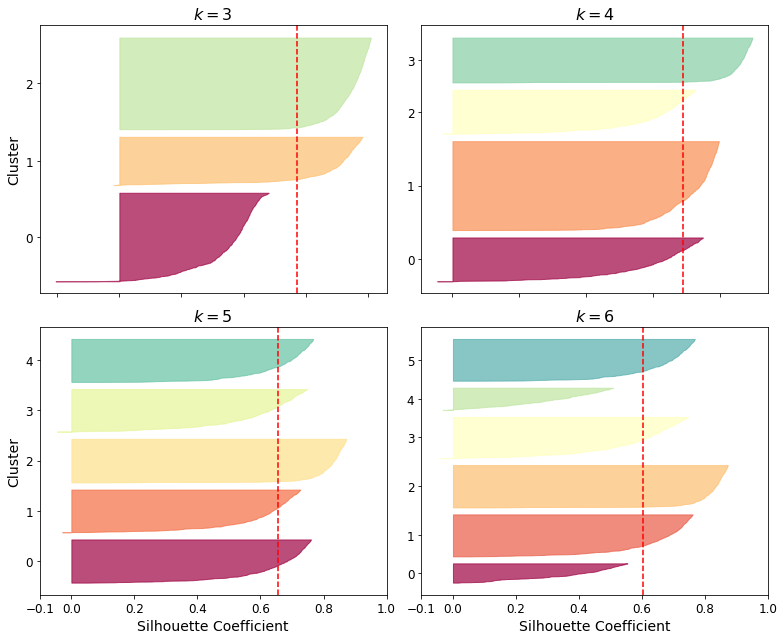
여기서는 k=4일 때 인덱스 1의 클러스터가 매우 큽니다. k=5일때는 대부분 비슷한 크기를 갖습니다. 따라서 k-4일 때 전반적인 실루엣 점수가 k=5보다 조금 높더라도 비슷한 크기의 클러스터를 얻을 수 있는 k=5를 선택하는 것이 좋습니다.
k-means 클러스터링에서 적절한 클러스터 개수(k)를 선택하는 것은 중요한 결정 사항 중 하나입니다. 여기서 언급한 상황에서 k=4와 k=5를 비교할 때, k=5를 선택하는 이유는 다음과 같습니다:
비슷한 크기의 클러스터를 얻을 수 있음: k=4일 때 인덱스 1의 클러스터가 매우 크다고 설명하셨는데, 이는 클러스터링 결과가 불균형하다는 것을 나타냅니다. 하나의 클러스터가 다른 클러스터보다 훨씬 크면, 클러스터링 결과가 편향되거나 불균형할 수 있습니다. k=5를 선택하면 클러스터의 크기가 비슷해지고, 데이터를 더 고르게 분할할 수 있습니다.
적절한 클러스터 개수 선택: k-means 클러스터링에서는 적절한 k 값을 선택하는 것이 중요합니다. 너무 적은 k 값은 클러스터를 너무 크게 만들어 데이터를 세분화하지 못하게 할 수 있고, 너무 많은 k 값은 불필요한 세분화로 이어질 수 있습니다. 따라서 데이터에 맞는 적절한 k 값을 선택하는 것이 중요합니다. k=5는 비슷한 크기의 클러스터를 얻을 수 있으면서도 데이터를 적절하게 분할하는 것으로 보입니다.
실루엣 점수 고려: 언급하신 대로, k=4일 때 전반적인 실루엣 점수가 k=5보다 조금 높다고 가정하겠습니다. 그러나 실루엣 점수는 하나의 지표일 뿐이며, 데이터에 대한 전체적인 이해를 제공하지는 않습니다. 클러스터의 크기와 불균형은 데이터의 복잡성을 고려할 때 중요한 요소이며, 적절한 k를 선택하는 데에도 영향을 미칩니다. 따라서 비슷한 실루엣 점수를 가진 k 값 중에서도 클러스터 크기와 불균형을 고려하여 선택하는 것이 바람직합니다.
종합적으로, k=5를 선택하는 것은 데이터를 더 고르게 분할하고 클러스터의 크기를 비슷하게 유지하면서 적절한 k 값을 선택하는 것으로 보입니다. 그러나 클러스터링은 데이터와 문제에 따라 다를 수 있으므로 최종 결정은 실제 데이터와 목적에 따라 조정해야 합니다.
1) 클러스터 개수를 실루엣계수와 다이어그램으로 정하기
2) 알고리즘 반복으로 centroid 찾기
2. k-평균의 한계
최적이 아닌 솔루션을 찾기 위해 알고리즘을 여러 번 반복 후 선택하게 됩니다. 또한 클러스터 개수를 지정해야 하며 클러스터의 크기나 밀집도가 서로 다르거나, 혹은 원형이 아닐 경우에는 잘 작동하지 않습니다!
따라서 타원형 클러스터 같은 경우는 잘 군집화하지 못 하고 이런 겨웅는 가우시안 혼합 모델을 사용해야 합니다.
그렇기에 k-평균은 실행 전에 스케일을 맞춰주는 것이 필수입니다.
3. 군집을 사용한 이미지 분할
이는 이미지에 있는 색상의 군집화를 통해 객체를 segmentation하는 것 입니다!
segmented_imgs = []
n_colors = (10, 8, 6, 4, 2)
for n_clusters in n_colors:
kmeans = KMeans(n_clusters=n_clusters, random_state=42).fit(X)
segmented_img = kmeans.cluster_centers_[kmeans.labels_]
segmented_imgs.append(segmented_img.reshape(image.shape))
---
plt.figure(figsize=(10,5))
plt.subplots_adjust(wspace=0.05, hspace=0.1)
plt.subplot(231)
plt.imshow(image)
plt.title("Original image")
plt.axis('off')
for idx, n_clusters in enumerate(n_colors):
plt.subplot(232 + idx)
plt.imshow(segmented_imgs[idx])
plt.title("{} colors".format(n_clusters))
plt.axis('off')
save_fig('image_segmentation_diagram', tight_layout=False)
plt.show()
4. 군집을 사용한 전처리
from sklearn.datasets import load_digits
X_digits, y_digits = load_digits(return_X_y=True)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X_digits, y_digits, random_state=42)
from sklearn.pipeline import Pipeline
pipeline = Pipeline([
("kmeans", KMeans(n_clusters=50, random_state=42)),
("log_reg", LogisticRegression(multi_class="ovr", solver="lbfgs", max_iter=5000, random_state=42)),
])
pipeline.fit(X_train, y_train)
pipeline_score = pipeline.score(X_test, y_test)
pipeline_score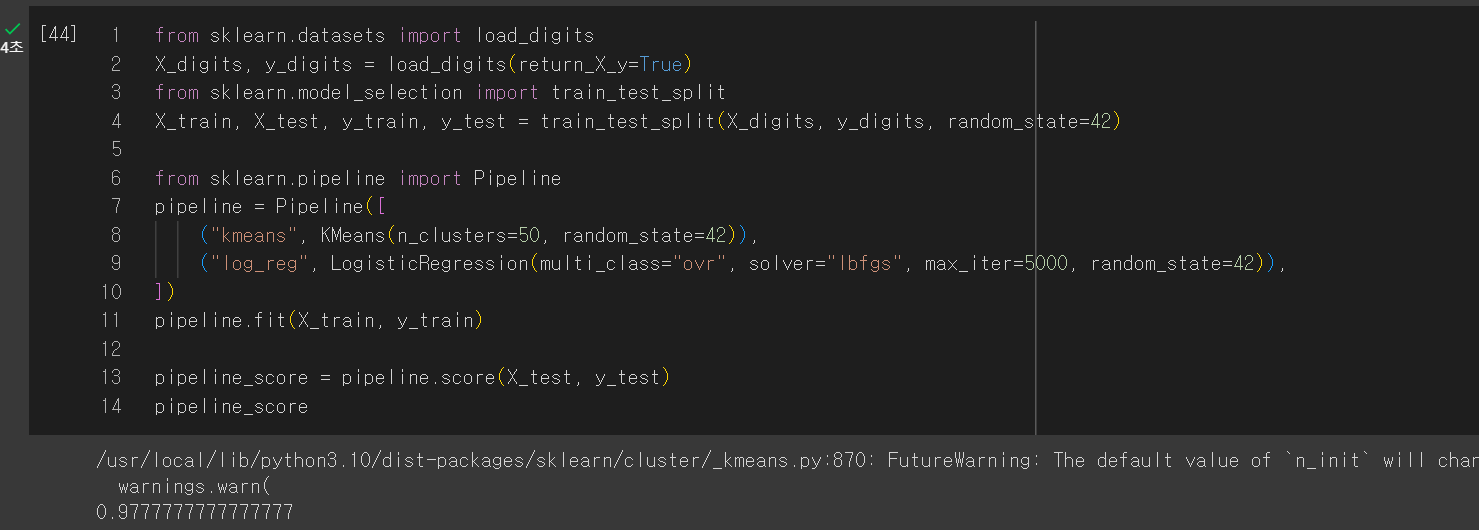
그리드 서치를 통해 최적의 파라미터를 찾을 수 있습니다.
from sklearn.model_selection import GridSearchCV
param_grid = dict(kmeans__n_clusters=range(2, 100))
grid_clf = GridSearchCV(pipeline, param_grid, cv=3, verbose=2)
grid_clf.fit(X_train, y_train)
---
grid_clf.best_params_
---
grid_clf.score(X_test, y_test)5. DBSCAN
이 알고리즘은 밀집된 연속적 지역을 클러스터로 정의합니다.
샘플에서 입실론 거리 내에 샘플이 몇 개 있는 지 셉니다. 적어도 min samples 개수만큼 있다면 이를 핵심 샘플이라고 합니다. 핵심 샘플의 이웃에 있는 모든 샘플은 동일한 클러스터에 속하게 됩니다. 그렇기에 DBSCAN은 클러스터 개수를 지정할 필요가 없습니다. 그리고 결과값을 가지고 특정 거리 이상은 이상치로 설정하기도 합니다.
from sklearn.cluster import DBSCAN
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=1000, noise=0.05)
dbscan = DBSCAN(eps=0.20, min_samples=5)
dbscan.fit(X, y)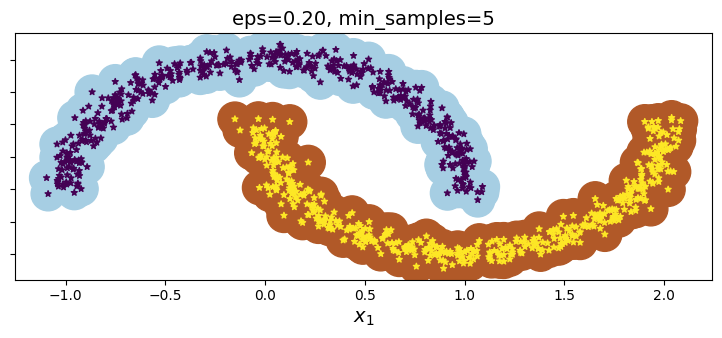
DBSCAN은 fit_predict로 새로운 샘플에 대해 클러스터를 예측할 수 없습니다.
따라서 이런 경우에는 DBSCAN의 결과값을 이용하여 KNN을 사용합니다.
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=50)
knn.fit(dbscan.components_, dbscan.labels_[dbscan.core_sample_indices_])
# 핵심 샘플, 클러스터 값
X_new = np.array([[-0.5, 0], [0, 0.5], [1, -0.1], [2, 1]])
knn.predict(X_new)
knn.predict_proba(X_new)하지만 단점으로는 클러스터 간의 밀집도가 크게 다르면 모든 클러스터를 올바르게 잡아내는 것은 불가능합니다.
추가적으로 다른 군집 알고리즘은
병합 군집, BIRCH, 평균-이동, 유사도 전파, 스펙트럼 군집 등이 있습니다.
