시계열 기본 이해

시계열 데이터의 이해

시계열(Time Series) 데이터

• 시간의 흐름에 따라 관측치가 변하는 데이터
  예) 따릉이 대여량 데이터
• 시간의 흐름에 따라 기록한 대여량 => 시계열 데이터
• 서비스 시작 이후 전체 대여량 => 일반 데이터

시계열 데이터 기본 모형

시계열 데이터는 일반 데이터에 시간이라는 속성이 더해진 경우이다. 따라서 통계적 관점에서 '시간'이라는 속성에 의해 발생하는 문제가 있다.

• 데이터의 평균/분산과 같은 속성이 시간의 흐름에 따라 변할 수 있다
• 이는 곧 같은 데이터의 집합에 서로 다른 속성을 갖는 데이터들이 모여 있다는 말(데이터의 비정상성) => 모델링을 어렵게 하는 요인이 됨
  - 기존 모형들은 데이터 모집단의 속성은 동일하다는 가정인 정상성(Stationarity)이 있는 데이터다 라는 가정이 깔려 있는 경우가 많기 때문이다. 쉽게 말하면 샘플링된 데이터의 평균과 분산이 모집단과 많이 다를 수 있기 때문에 일반적인 모델링 모형들은 데이터의 트렌드를 반영하지 못할 수 있다. 전체 데이터의 평균과 분산으로 판단하고 가정을 세우면 안된다. 시간의 흐름에 따라서 같은 데이터 안에 다른 속성을 가진 데이터가 모여 있기 때문에 이들의 평균과 분산이 다르고 모델링이 어려워지는 원인이 된다.
  

• '시간'의 변화에 따라서 어떤 특성들로 인해 속성이 변하게 되는 것인가
  - 시계열에는 전통적인 연구에서 밝혀진 다음과 같은 3개의 성분(component)이 존재함
  

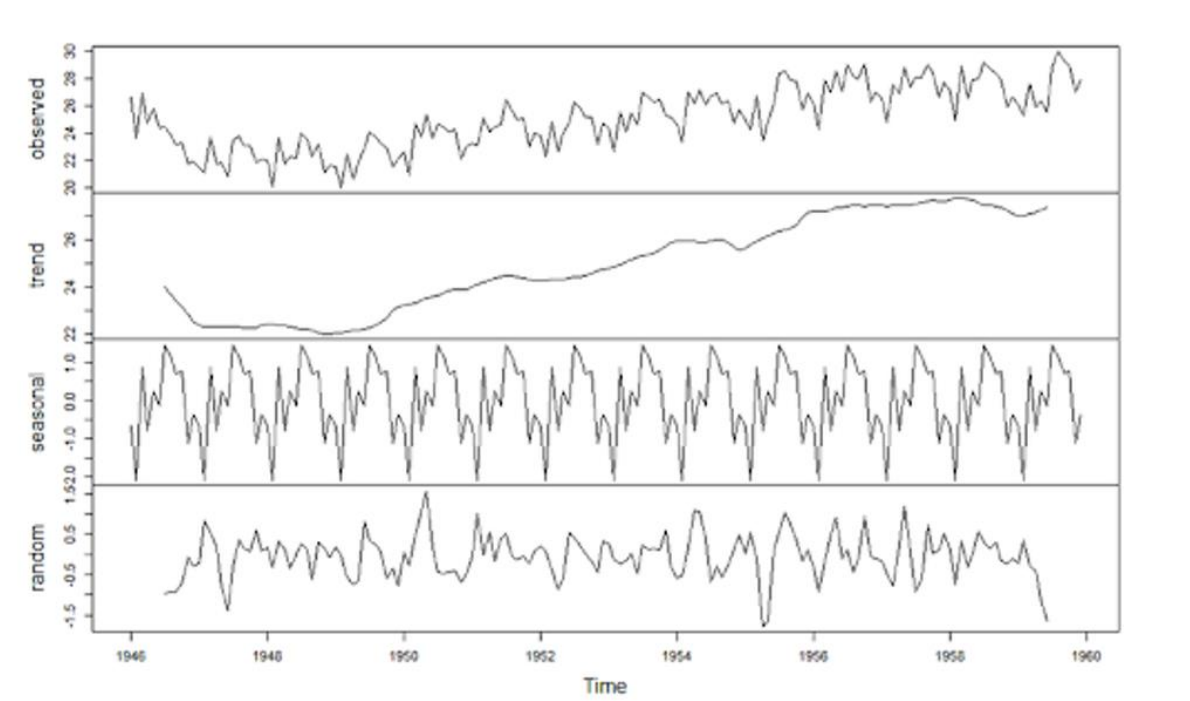
  - 추세성분(Trend Component) : 관측한 데이터가 움직이는 형태, 추세 성분에 따라서 평균값의 변화(레벨의 차이)가 나타남
  - 계절성분(Seasonal Component) : 일정한 주기의 반복, 계절 성분에 따라 분산의 값이 달라짐
  - 불규칙 성분(Irregular or Residual Component) : 시간의 흐름에 따라서 데이터가 가진 본연의 성질이 나타남
  

시계열 분해(Time Series Decomposition)

전통적인 시계열 모델의 관점에서 앞에서 설명한 3가지 속성(추세, 계절, 불규칙)의 결합으로 시계열을 표현할 수 있다.
즉, $y_t = S_t + T_t + R_t$ or $y_t = S_t \times T_t \times R_t$이고
시계열에서 각각의 성분을 구할 수 있다면, 원래 시계열에서 특정 성분을 제거하는 것이 가능하다. 즉, $y_t = S_t + T_t + R_t$라고 가정했을 때, 추세를 제거한 시계열은 $detrend = timeseries - trend$로 계산이 가능하다.

• 대다수의 시계열이 정상성(=특성이 시간의 흐름에 따라 변하지 않음)을 갖지 못하는 이유
  - 시계열 데이터의 추세, 계절성 같은 고유의 특성 때문
  • 이러한 시계열 데이터의 고유 특성을 제거할 수 있다면 정상성을 갖는 시계열로 바꿀 수 있고 이것이 시계열 분해를 수행하는 이유이다.

정상성과 비정상성(Stationarity / Non-Stationarity)

정상 시계열 : 시간의 흐름에 무관하게 일정한 평균 / 분산을 가짐
비정상 시계열 : 시간의 흐름에 따라 변동적인 평균 / 분산을 가짐
강한(Strict) 정상성 : 위에서 내린 정상 시계열의 정의(현실적으로 거의 존재하지 않음)
약한(Weak) 정상성 : 평균은 일정하고, 시간에 종속적이지 않으나, 분산은 "시차"에 따라 변함

자기상관 (Auto-Correlation)

시계열의 정상 / 비정상 여부를 판단하는 방법

• 정상 시계열은 어느 시계열 구간에서 관찰하든 평균과 분산이 일정
• 관측값 간의 공분산도 일정
• 즉, 시계열 구간 간의 상관관계(Correlation)가 일정하다는 말

자기상관(Auto-Correlation)

• 동일 변수를 시점을 달리하여 관찰하였을 때 관측값들 사이의 상호 관련된 정도(Correlation)를 나타내는 척도

자기상관의 계산 방법

• 시차(Lag)를 적용해서 계산
• Lag는 특정 시차만큼 관측값을 뒤로 이동시키는 것을 의미함
• 시차=1,2,3...을 적용한 데이터와 시차가 0(=원본)인 데이터의 상관관계를 구하면 시차의 변화에 따라 자기상관을 계산할 수 있음

정상 시계열은 자기상관이 시간에 따라 변화하지 않는다는 특징이 있음

자기상관함수(ACF)

시차=1,2,3,...k에 대한 일련의 자기상관을 구하는 함수를 ACF(Autocorrelation Function)이라고 하며 이는 시차에 따른 관측값 간의 연관 정도를 나타낸다.

• 정상 시계열의 경우
  - ACF는 빠르게 0으로 감소함
  - 약한 정상의 경우 분산이 시차에 따라 변하기 때문
  

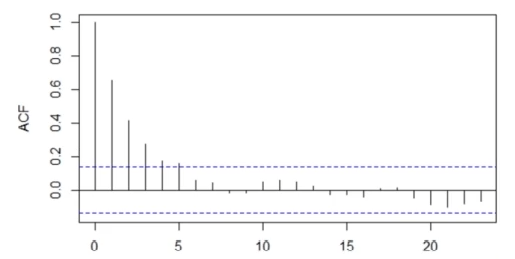
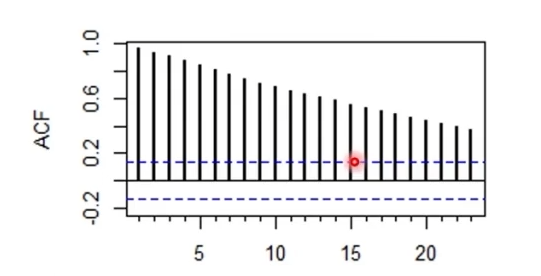
• 비정상 시계열의 경우(공분산 값이 시차에 따라 일정하지 않은 트렌드를 가짐)
  - ACF는 천천히 감소하며, 큰 값을 가지는 경우가 많음
  

정상 시계열 변환

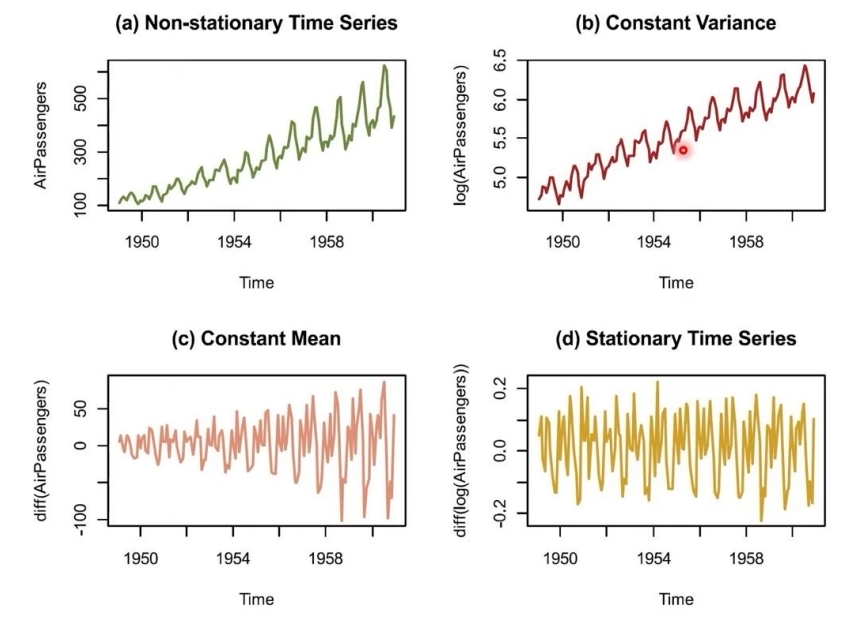
ACF를 통해 비정상 시계열로 판단된 시계열은 정상 시계열로 변환하는 작업을 거침

• 변동폭이 일정하지 않으면 로그(Log)를 씌워 분산을 일정하게 유지되도록 변환
• 추세 / 계절적 요인이 관찰되면 차분(differencing)을 수행해 평균이 일정하게 유지되도록 변환
  - 차분 : 시계열 $y_t$의 관측값을 $y_t-y_{t-1}$로 대체
• 위 두 케이스에 모두 해당하는 경우 => 로그와 차분을 모두 수행
  

정상 시계열 예측 모델 - ARIMA

시계열이 정상 시계열이라면 평균과 분산이 일정하다. 이러한 통계적 특성을 기반으로 모델링을 수행할 수 있는데 정상 시계열을 가장 잘 모델링하는 모델 중 하나는 ARIMA 모델이다. AR(AutoRegressive)과 MA(Moving Average) 모델을 결합한 모델로 ARIMA를 이해하기 위해서는 AR과 MA 모델에 대한 이해가 필요하다.

AR(Autoregressive Model)

자기회귀 모델로 과거 관측값을 이용해 현재 혹은 미래의 값을 설명하는 모델이다.

$y_t = c+\phi_1y_{t-1}+\phi_2y_{t-2}+\cdots+\phi_py_{t-p}+\varepsilon_t$

정상 시계열이라면 평균과 분산이 일정하기 때문에 과거 데이터의 선형 결합으로 현재 혹은 미래의 값을 설명할 수 있고 일반적으로 AR(p)로 표기한다.(p=window)

MA(Moving Average Model)

시계열이 약한 정상 시계열이라면, 특정 시점 t의 값은 평균이 $\mu$, 표준편차가 $\sigma$인 백색 잡음(white noise)으로 생성한 시계열과의 error의 조합으로 표현할 수 있다. 이유는 평균은 일정하고 공분산은 '시차'에만 영향을 받기 때문이다. MA 모델을 통해 시계열 데이터의 불확실성을 어느 정도 반영할 수 있고, 설명력이 약한 케이스에 이 모델을 적용하면 효과적이다.

$Z_t = a_t-\theta_1a_{t-1}-\theta_2a_{t-2}-\cdots-\theta_pa_{t-p}$

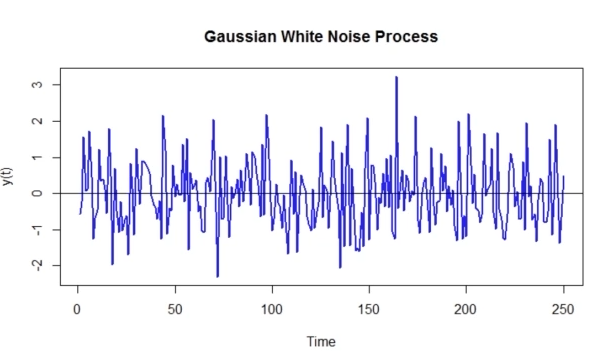
일반적으로 MA(q)로 표기한다. (q=window)

ARIMA(AutoRegressive Integrated Moving Average)

ARIMA는 AR과 MA 모델을 결합한 모델로 차분(differencing)하여 결합한 모델이다.

• AR(p) + MA(q)를 d만큼 차분한 모델
• AR 혹은 MA로만 데이터를 설명하는 것보다 훨씬 더 높은 설명력을 가짐
• 데이터에 추세, 계절성이 관찰될 때, 차분을 하면 데이터를 정상 시계열로 변환 가능

SARIMA(Seasonal ARIMA)

ARIMA 모델에 계절성 시계열을 추가로 모델링하여 더한 것이다.

• ARIMA(p,d,q) + S(p,d,q) = SARIMA
• 일반적으로 데이터에 추세만 있는 경우 ARIMA 사용
• 추세 + 계절성이 동시에 있는 경우는 SARIMA를 써서 모델링함

ARIMA 예측 과정 : Box-Jenkins Procedure

ARIMA 모델을 이용한 시계열 예측은 다음과 같이 진행할 수 있다.

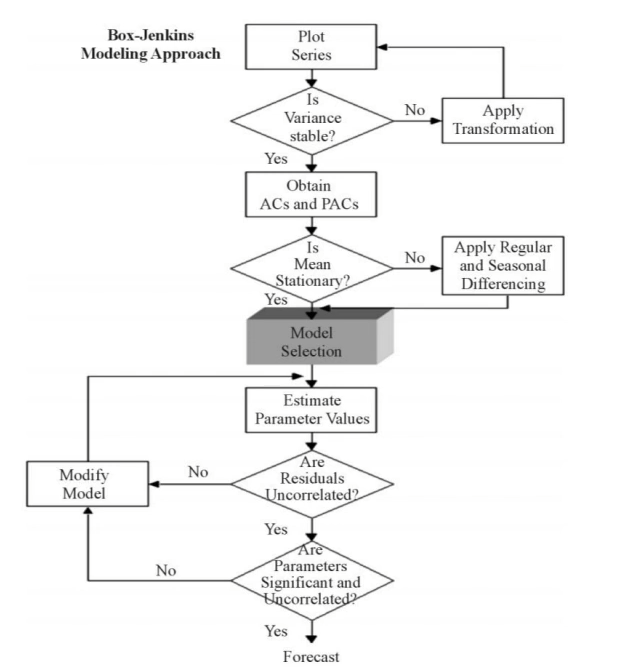
• 데이터 확인(정상성 체크)
  - 정상 시계열이 아니라면 변환(로그/차분)
• 모델 선택
• 결과 확인
• 만족스러운 결과가 나올 때까지 반복
  위와 같은 과정을 Box-Jenkins Procedure라고 함