시계열 데이터 전처리

결측치(Missing Values)

결측치는 일반적인 데이터에서도 어떻게 처리하는지가 정말 중요한 이슈이지만, 시계열 데이터에서는 그 중요도가 더욱 올라간다. 그 이유는 대부분의 시계열은 비정상(구간별로 다른 특성을 가지는)이기 때문에 시간에 따라 평균과 분산이 변한다. 따라서 특정 시점 값의 소실은 그 시점의 평균과 분산의 왜곡을 가져오고 결과적으로 분석 결과에 치명적인 영향을 미치게 되는 것이다.
실제 비즈니스 상황에서 우리가 접하는 거의 모든 데이터에는 항상 결측치가 발생한다. 특히 시계열의 경우 시간의 흐름에 따라 그때 그때 수집하는 경우가 많기 때문에 결측치가 더 자주 생기며 아래와 같은 문제 상황이 발생하는 경우도 결측치가 발생한다.

• 네트워크 이슈로 갑자기 로그 수집이 끊겨서 복구가 안되는 경우
• 센서의 정지로 일정 기간 동안 데이터 수집이 아예 되지 않는 경우
• 실시간으로 주가 데이터 수집 중에 네트워크 이슈로 일정 기간 수집하지 못한 경우

더해서 시계열 데이터의 결측치는 일반적인 데이터와 처리 방법이 달라 시계열 데이터의 결측치를 어떻게 처리하는지 알아야 한다.

일반 데이터의 결측치 처리 방법

일반 데이터에 결측치가 발생한 경우, 두가지 선택이 가능하다.

• 해당 결측치가 포함된 레코드 전체를 삭제(drop na value)
• 해당 결측치를 산입(imputation)
  - imputation : 불완전한 데이터가 있을 때 표준이나 대표성이 있는 다른 데이터를 활용하여 대체될 수 있는 값들로 계산하여 입력하는 과정

대표적인 imputation 방법론

• mean/median imputation : 결측값을 결측되지 않은 나머지 값들의 평균이나 중앙값으로 대체
• most frequent value imputation : 최빈값으로 대체
• ML imputation : 결측값을 맞추는 모델을 만들어 대체

시계열 데이터의 결측치 처리 방법

단순 평균/중앙값/최빈값으로 결측치를 처리하는 것은 바람직한 방법이 아니다. 왜냐하면 시계열 데이터는 비정상성으로 인해 시간의 흐름에 따라 데이터의 평균과 분산이 변하기 때문이다. 이러한 특징을 알고 잘 반영하는 방법론을 활용해야 성공적으로 imputation을 수행할 수 있고 이것이 시계열 imputation의 핵심이다.

단순하지만 효과적인 시계열 결측치 처리 방법들

• Last observation carried forward(LOCF) : 직전 관측치 값으로 결측치를 대체
• Next observation carried backward(NOCB) : 직후 관측치 값으로 결측치를 대체
• Moving Average / Median : 직전 N의 time window의 평균치 / 중앙값으로 결측치를 대체

조금은 복잡한 방법들

보간법(interpolation)

• 통계적으로 이미 구해진 데이터들로부터 주어진 데이터를 만족하는 근사 함수를 구하는 방법론
• 선형 / 비선형 / 스플라인 보간법 등이 존재
• 근사 함수를 만들어 선을 잇고, 어떤 근사 함수를 쓸지 결정하기만 하면 됨
• 선형 보간법 : 근사 함수가 선형(Linear) 함수임을 가정
• 비선형 보간법 : 근사 함수가 비선형(non-linear) 함수임을 가정
• 스플라인(spline) 보간법 : 전체 구간을 근사하는 것이 아닌, 소구간을 나눠서 보간

가장 복잡하고 어려운 방법

모델링(Modeling)
결측치를 맞추는 모델을 만든다.

• 일반적인 데이터라면 기존 데이터들이 결측치를 잘 설명할 가능성이 높아 조금은 수월
• 시계열의 경우 시간에 따라 평균과 분산이 다르기 때문에, 모델링을 하기에는 데이터가 충분치 않을 가능성이 높다.
• 최근에는 GAN을 이용한 시계열 데이터 생성 알고리즘으로 이를 대체하려는 시도 등장

노이즈(Noise)

노이즈는 잡음을 뜻하며 데이터에서 노이즈란 다른 외부 요인의 간섭과 같은 여러 가지 의도하지 않은 데이터의 왜곡을 불러오는 모든 것을 의미한다. 즉, 시계열의 원래 분포를 왜곡하는 모든 요인이라고 이해하면 편하다.

노이즈의 예시

• 센서 자체에서 발생하는 신호의 간섭
• 매출 로그 데이터에 발생한 일시적 이상 기록(구글 앱스토어 버그 등)과 같은 이상치들

노이즈는 특시 시계열 데이터 분석에 있어 치명적인 영향을 끼치는데 시계열 데이터의 경우 전체 데이터가 아닌 특정 구간의 데이터를 보기 때문에 시간의 흐름에 따라 변화하는 통계적 특성을 강하게 왜곡한다. 결측치와 마찬가지로 시간 순대로 기록되는 정보이기에 일반 데이터에 비해 시계열 데이터에 노이즈가 같이 기록될 가능성도 높고 일반적인 데이터와 노이즈 제거 방법도 다르다.

시계열 데이터의 노이즈 처리 방법

시계열 데이터의 노이즈 제거를 Denoising이라고 한다.

가장 간단한 Denoising 방법

Moving Average

• 평균값으로 관측치를 대체하면 이상하게 튀는 값들을 평활화할 수 있음
• 노이즈가 정말 많은 환경에서는 노이즈 자체가 평균이 되버리는 경우도 있어서 적합하지 않음
• 노이즈가 간혹 발생하는 경우에는 매우 효과적

노이즈가 너무 많은 경우 - Smoothing or Filtering

• 현재 시계열에 발생하는 노이즈가 어떤 특정한 분포를 따른다고 가정하고 해당 분포의 값을 시계열에서 제거
• 즉, 시계열이 다음과 같이 표현된다고 가정
  $x_{n+1} = A_{x_n} + \xi$
• 여기서 $\xi$(노이즈) 가 어떤 특정한 분포를 따른다고 가정하고, 이를 근사한 값을 제거함으로써 원래 값을 복원

대표적인 필터링 방법

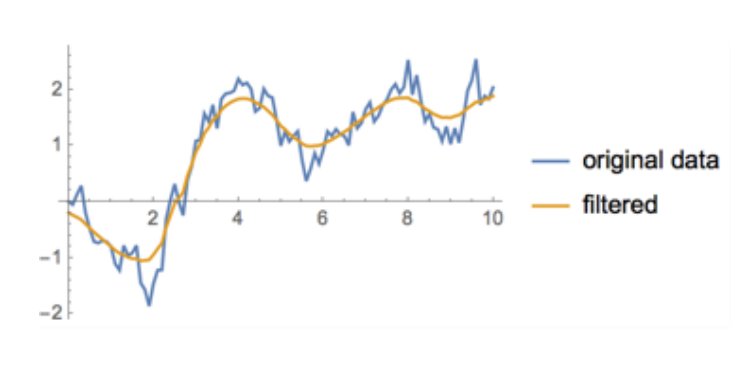
• 가우시안 필터링(Gaussian Filtering)
  - 노이즈가 정규분포를 따른다고 가정함(일반적으로 노이즈는 정규분포를 따름)
• 쌍방 필터(Bilateral Filter)
  - 변곡점이 큰 지점을 뭉개버린다는 특징을 갖는 가우시안 필터링의 단점을 보완
  -> 데이터의 원 분포에 따라 발생하는 엣지(edge)들을 더 잘 보존할 수 있음
• 칼만 필터(Kalman Filter)
  
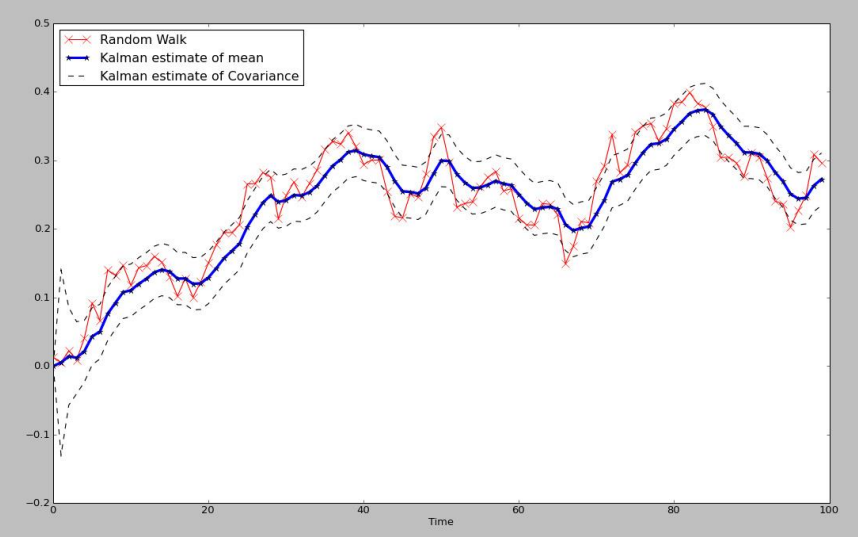
  - 현재 상태의 결합분포를 추정하는 모델링 알고리즘으로 잡음이 포함된 과거 측정값에서 현재 상태의 결합분포를 추정하는 알고리즘
  - 일반화된 분포를 가정하는 것이 아닌 데이터의 특성에 맞는 분포를 모델링할 수 있어 상당히 많이 사용되는 알고리즘

필터링의 통계적 특성까지 모두 이해하면 좋기는 하지만 시계열에서의 노이즈 처리의 중요성과 방법론의 원리만 파악해도 현업에서 적용은 가능하다.