🛍️ 배낭 문제란?

• 배낭에 담을 수 있는 무게의 최대값이 정해져 있고
• 일정한 가치와 무게가 정해져 있는 짐들을 배낭에 담을 때

가치의 합이 최대가 되도록 짐을 고르는 방법을 찾는 문제

• 짐을 쪼갤 수 있는 경우(짐의 무게가 소수일 수 있는 경우)- 분할 가능 배낭 문제(Fractional)
• 짐을 쪼갤 수 없는 경우(짐의 무게는 0 이상의 정수만 가능) - 0-1 배낭 문제(0-1 Knapsack)

두 가지로 나눌 수 있고, 주로 0-1 배낭 문제가 다루어진다.

🛍️ 0-1 배낭 문제

0-1 배낭 문제는 DP를 사용하는 기본적인 문제이다.

1️⃣ 완전 탐색

• 모든 경우의 수를 다 계산해본다.

n개의 짐이 있다고 할 때, 만들 수 있는 부분 집합은 $2^n$개이다.
시간 복잡도가 $O(2^n)$이므로 너무 느리다.

2️⃣ 그리디 알고리즘

• 가치가 큰 짐 또는 무게가 큰 짐부터 먼저 골라서 넣어 본다.
  

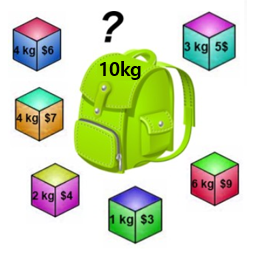
그림과 같이 짐과 가방이 있고, 가격이 비싼 짐부터 고르는 상황을 가정해보자.

6kg / $9와 4kg / $7을 고르고, 가격은 총 $16이 된다.

하지만, 그림을 유심히 보면 4kg / $6, 4kg / $7, 4kg / $4를 고르면 $17이 되기 때문에 그리디 알고리즘으로는 최적의 답을 구할 수 없다는 것을 알 수 있다.

3️⃣ DP

• i번째 짐을 넣었을 때 배낭의 최대 무게를 넘으면, i-1번째까지의 짐을 가지고 구한 최적의 가치가 최대
• i번째 짐을 넣었을 때 배낭의 최대 무게를 넘지 않으면, i-1번째까지의 짐을 가지고 구한 최적의 가치 + i번째 짐의 가치와 i-1번째까지의 짐을 가지고 구한 최적의 가치 중 더 큰 값을 선택

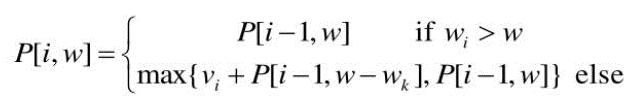
• P[i, w]는 i개의 짐이 있고, 배낭의 최대 무게가 w일 때 최대 이익을 의미한다.

• i가 0인 경우는 짐을 0개 넣은 것을 의미하므로 모두 0
• w가 0인 경우 배낭에 짐을 넣지 못하는 것을 의미하므로 모두 0

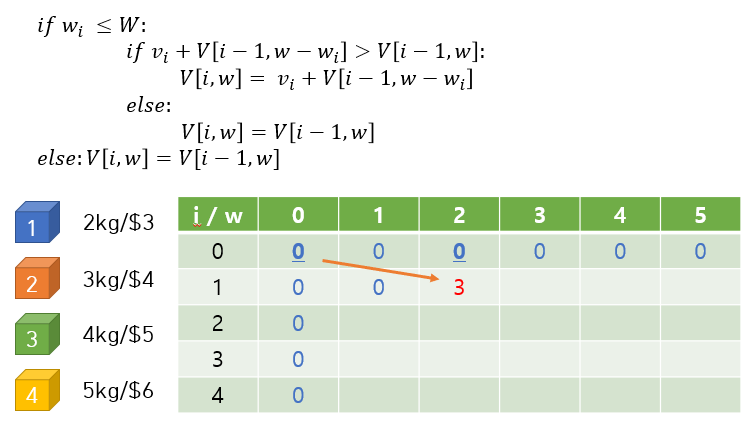
• 첫 번째 짐인 2kg/$3를 고려
• w=1일 때는 짐을 넣지 못하므로 V[1, 1] = 0
• w=2일 때는 짐을 넣을 수 있고, V[0, 2]보다 V[0,0]+3이 크므로 V[1, 2] = V[0,0]+3 = 3이 됨
• w=3, 4, 5여도 더 넣을 짐이 없으므로 모두 3이 됨

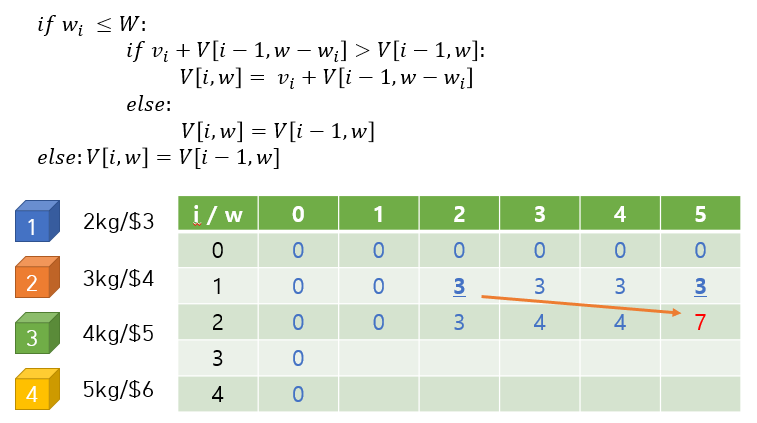
• 두 번째 짐인 3kg/$4
• w=0, 1, 2일 때는 3kg을 수용하지 못하므로, V[1, w]일 때와 값이 동일
• w=3일 때, 짐을 넣은 경우가 크므로 V[2][3] = 4
  • 짐을 넣을 경우: 4 + V[1][3-3] = 4
  • 짐을 안 넣을 경우: V[1][3] = 3

이렇게 반복하면서 표를 채우면, 마지막 칸이 결국 모든 짐들을 확인했을 때의 무게 w에서 구할 수 있는 최적의 이익이 된다.

0-1 배낭 문제의 대표적인 문제는 백준 12865번 평범한 배낭이다.

🛍️ 분할 가능 배낭 문제

분할 가능 문제에서는 4kg/$8인 짐이 있다면 2kg/$4, 2kg/$4로 짐을 분할하여 배낭에 담을 수 있다.

해당 문제는 그리디 알고리즘으로 무게 대비 가치가 높은 물건부터 담는 방법으로 간단하게 풀 수 있다.

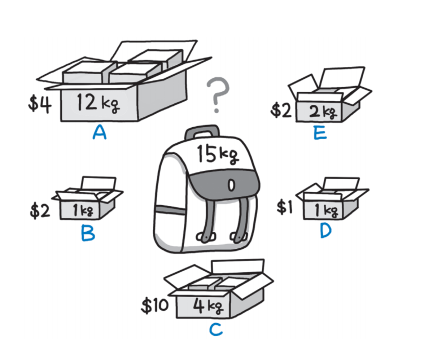
그림과 같이 짐과 가방이 있다고 가정해보자. 각 짐의 무게 대비 가치는 아래와 같다.

• A: $0.333/kg
• B: $2/kg
• C: $2.5/kg
• D: $1/kg
• E: $1/kg

이 때, 1kg을 단위로 C > C > C > C > B > D > E > E > A > A > A > A > A > A > A

순서로 담으면 총 $17.333을 담을 수 있다.

cargo = [
(4, 12),
(2, 1),
(10, 4),
(1, 1),
(2, 2)
]

def fractional_knapsack(cargo):
	capacity = 15
    pack = []
    for c in cargo:
    	pack.append((c[0]/c[1], c[0], c[1]))
    pack.sort(reverse = True)
    
    total_value: float = 0
    for p in pack:
    	if capacity - p[2] >= 0:
        	capacity -= p[2]
            total_value += p[1]
            
        else:
        	fraction = capacity / p[2]
            total_value += p[1] * fraction
            break
            
	return total_value