03.유의성검정

기본 개념 (추가)

• 변수: 대상의 속성이나 특성을 측정하여 기록한 것
• 독립변수: 원인이 되는 변수로, 설명변수
• 종속변수: 결과가 되는 변수로, 결과변수
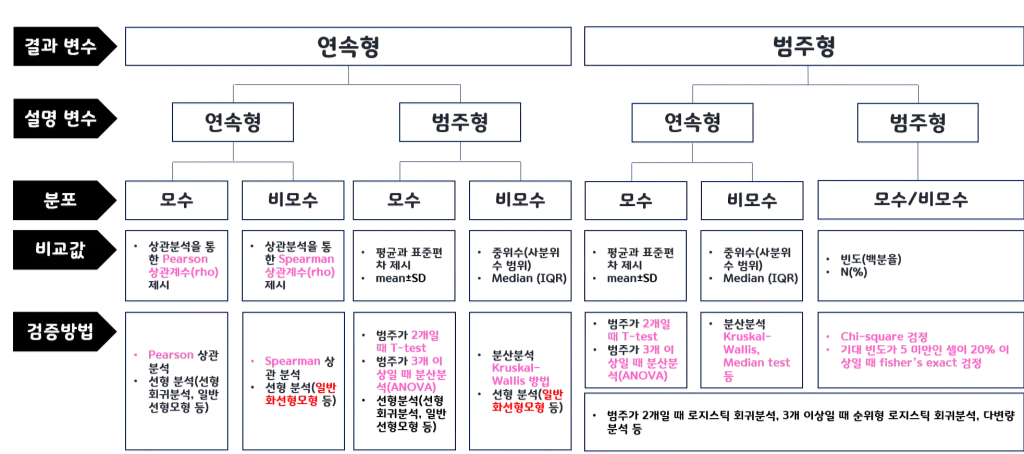
  독립변수에 따라 그 값이 변할 것이라고 예상하는 변수
• 모수: 모집단을 대표하는 값
• 모수통계: 모집단이 정규분포를 따른다는 가정하에 사용
  데이터분석가는 주로 모수통계를 진행
  평균, 분산 등의 값을 알고 있다는 가정 하에 진행하는 통계분석
• 비모수통계: 모집단이 정규분포가 아닐 때 사용
  (이 말은 곧 표본의 크기가 충분히 크지 않음: 소규모 실험에 해당).또는 평균, 분산 등의 값을 가정하지 않고 진행하는 통계분석

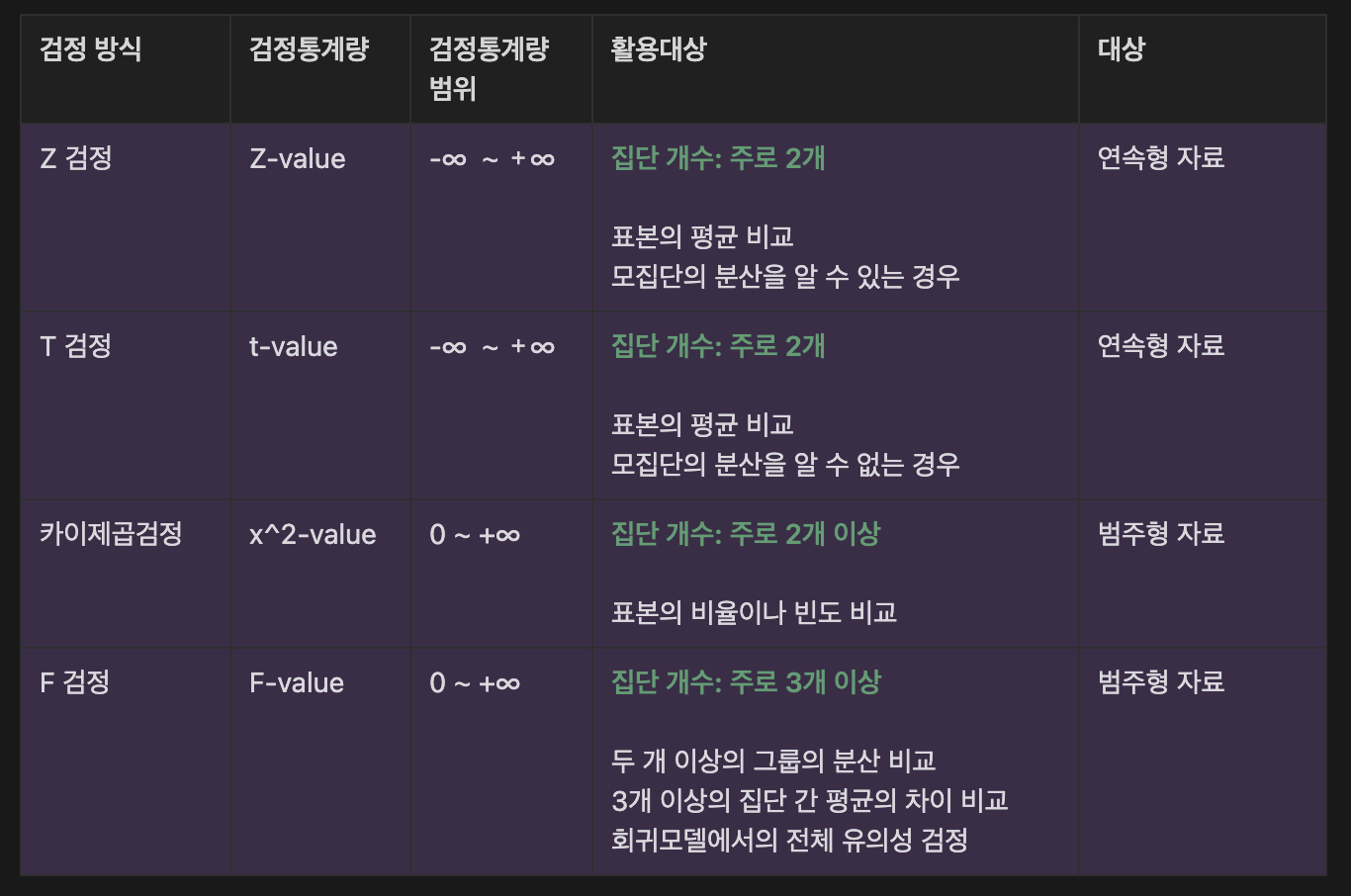
검정 방식 정리 (추가)

3.1 A/B 검정

A/B 테스트 정의 및 목적

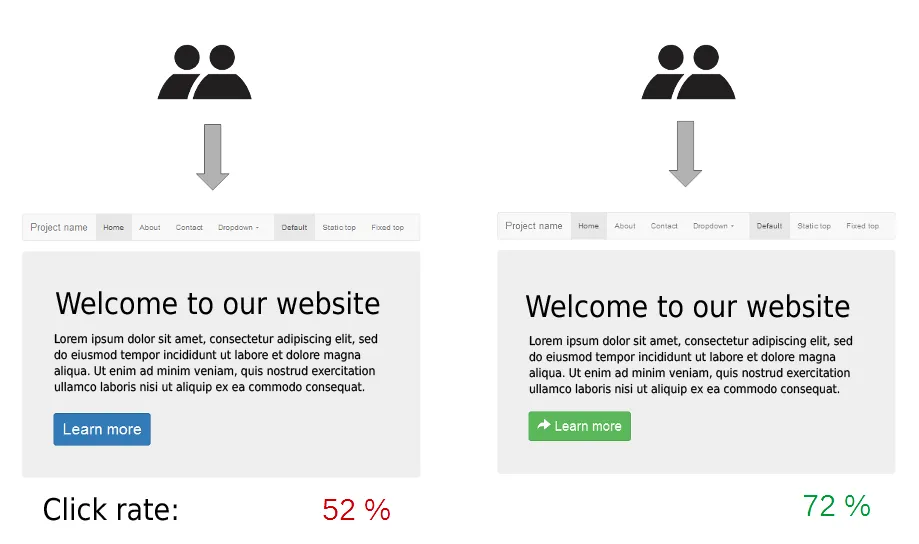
• A/B 검정은 두 버전(A와 B) 중 어느 것이 더 효과적인지 평가하기 위해 사용되는 검정 방법
• 마케팅, 웹사이트 디자인 등에서 많이 사용됨
• 사용자들을 두 그룹으로 나누고, 각 그룹에 다른 버전을 제공한 후, 반응을 비교
• 일반적으로 전환율, 클릭률, 구매수, 방문 기간, 방문한 페이지 수, 특정 페이지 방문 여부, 매출 등의 지표를 비교
• 두 그룹 간의 변화가 우연이 아니라 통계적으로 유의미한지를 확인

실제 사례

🍀 두 개를 비교하여 구매 전환율이 큰 것을 선택

• 온라인 쇼핑몰에서 두 가지 디자인(A와 B)에 대한 랜딩 페이지를 테스트하여 어떤 디자인이 더 높은 구매 전환율을 가져오는지 평가

<코드 예시>

import numpy as np
import scipy.stats as stats

# 가정된 전환율 데이터
group_a = np.random.binomial(1, 0.30, 100)  # 30% 전환율
group_b = np.random.binomial(1, 0.45, 100)  # 45% 전환율

# t-test를 이용한 비교
t_stat, p_val = stats.ttest_ind(group_a, group_b)
print(f"T-Statistic: {t_stat}, P-value: {p_val}")

<코드 설명>

• ❓ stats.ttest_ind
  - scipy.stats.ttest_ind 함수는 독립표본 t-검정(Independent Samples t-test)을 수행하여 두 개의 독립된 집단 간 평균의 차이가 유의미한지 평가
  - 이 함수는 두 집단의 데이터 배열을 입력으로 받아서 t-통계량과 p-값을 반환
  - t-통계량 (statistic)
  - t-검정 통계량-> 두 집단 간 평균 차이의 크기와 방향을 나타냄
  - p-값 (pvalue)
  - p-값은 귀무 가설이 참일 때, 현재 데이터보다 극단적인 결과가 나올 확률
  - 이 값이 유의수준(α) 보다 작으면 귀무 가설을 기각하고 이 값이 유의수준(α) 보다 크면 귀무 가설을 기각하지 않음

  👅 p값이 유의수준보다 작으면 내가 주장하는 가설을 채택한다고 이해!
  p값이 작은게 좋은거임!!

A/B 테스트 주의사항

• 적절한 표본 크기: 표본의 크기가 충분하지 않으면 유의미한 결과를 얻을 수 없음
  -> 적절한 표본 크기를 결정하고, 그에 맞는 시간과 자원을 투자해야 함
• 하나의 변수만 변경: A/B 테스트에서는 하나의 변수만을 변경해야 함
  -> 두 가지 이상의 변수를 동시에 변경하면 어떤 변수가 영향을 미쳤는지 파악할 수 없음
• 무작위성: A/B 테스트는 무작위로 선택된 사용자들에게 각각 다른 변수를 적용해야 함
• 적절한 분석 방법: A/B 테스트 결과를 해석할 때는 가설 검증을 위한 통계적 분석 방법을 선택하고, 유의수준을 설정해야 함
• 테스트 결과의 의미: A/B 테스트 결과가 통계적으로 유의미하더라도 항상 실제로 의미 있는 결과인지 한번 더 생각해보아야 함
• 정해진 기간 동안 진행: A/B 테스트는 동일한 기간 동안 진행되어야 함, 그 기간 동안에만 결과를 수집하고, 분석해야 함
  -> 너무 짧은 기간 동안에는 결과를 수집하기 어렵고, 너무 긴 기간 동안에는 사용자들의 행동이 변할 가능성이 있음

3.2 가설검정

데이터가 특정 가설을 지지하는지 검정하는게 포인트!

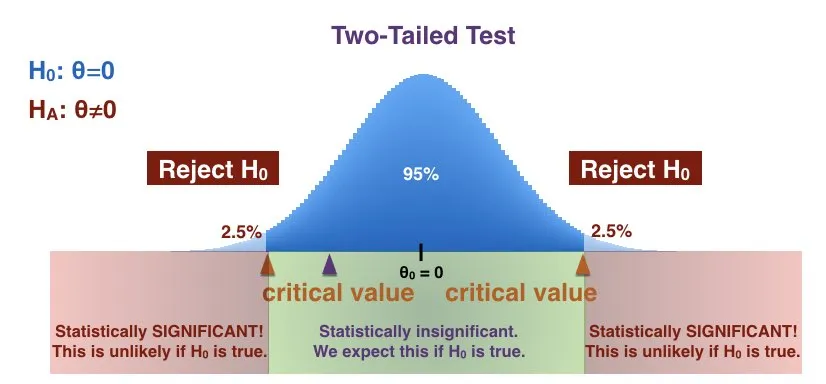
가설검정 정의

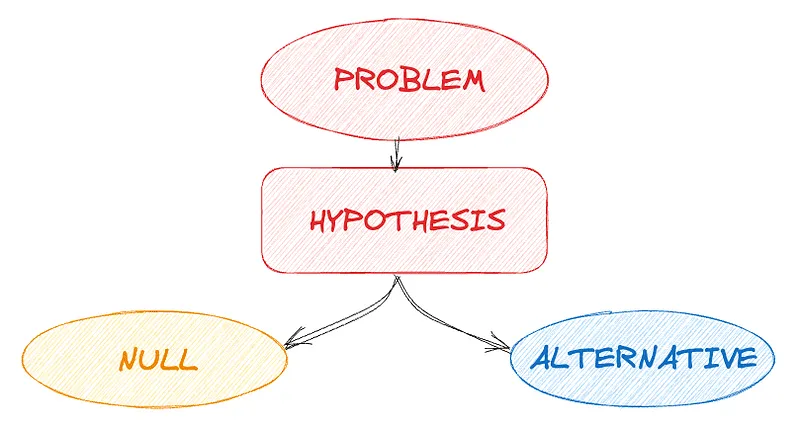
• 표본 데이터를 통해 모집단의 가설을 검증하는 과정
• 즉, 데이터가 특정 가설을 지지하는지 평가하는 과정
• 귀무가설(H0)과 대립가설(H1)을 설정하고, 귀무가설을 기각할지를 결정
• 데이터 분석시 두가지 전략을 취할 수 있음
  • 확증적 자료분석
    • 미리 가설들을 먼저 세운 다음 가설을 검증해 나가는 분석
  • 탐색적 자료분석(EDA)
    • 가설을 먼저 정하지 않고 데이터를 탐색해보면서 가설 후보들을 찾고 데이터의 특징을 찾는 것

가설검정 단계

1. 귀무가설(H0)과 대립가설(H1) 설정
2. 유의수준(α) 결정
3. 검정통계량 계산
4. p-값과 유의수준 비교
5. 결론 도출

통계적 유의성과 p값

• 통계적 유의성
  • 통계적 유의성은 결과가 우연히 발생한 것이 아니라 어떤 효과가 실제로 존재함을 나타내는 지표
  • p값은 귀무 가설이 참일 경우 관찰된 통계치가 나올 확률을 의미
  • 일반적으로 p값이 0.05 미만이면 결과를 통계적으로 유의하다고 판단
•  p-값
  • 귀무가설이 참일 때, 관찰된 결과 이상으로 극단적인 결과가 나올 확률
  • 일반적으로 p-값이 유의수준(α)보다 작으면 귀무가설을 기각
  • 유의수준으로 많이 사용하는 값이 0.05
• p-값을 통한 유의성 확인
  • p-값이 0.03이라면, 3%의 확률로 우연히 이러한 결과가 나올 수 있음
  • 일반적으로 0.05 이하라면 유의성이 있다고 봄

신뢰구간과 가설검정의 관계

• 신뢰구간과 가설검정은 밀접하게 관련된 개념
• 둘 다 데이터의 모수(ex. 평균)에 대한 정보를 구하고자 하는 것이지만 접근 방식이 다름
• 신뢰구간
  • 특정 모수가 포함될 범위를 제공
  • 신뢰구간이란?
    • 신뢰구간 (Confidence Interval)
    • 신뢰구간은 모집단의 평균이 특정 범위 내에 있을 것이라는 확률을 나타냄
    • 일반적으로 95% 신뢰구간이 사용되며, 이는 모집단 평균이 95% 확률로 이 구간 내에 있음을 의미
    • 만약 어떤 설문조사에서 평균 만족도가 75점이고, 신뢰구간이 70점에서 80점이라면, 우리는 95% 확률로 실제 평균 만족도가 이 범위 내에 있다고 말할 수 있음
• 가설검정
  • 모수가 특정 값과 같은지 다른지 테스트

실제 사례

• 새로운 약물이 기존 약물보다 효과가 있는지 검정
• 이 때 새로운 약물은 기존 약물과 큰 차이가 없다는 것이 귀무가설!
• 대립가설은 새로운 약물이 기존 약물과 대비해 교과가 있다는 것!

<코드 예시>

# 기존 약물(A)와 새로운 약물(B) 효과 데이터 생성
A = np.random.normal(50, 10, 100)
B = np.random.normal(55, 10, 100)

# 평균 효과 계산
mean_A = np.mean(A)
mean_B = np.mean(B)

# t-검정 수행
t_stat, p_value = stats.ttest_ind(A, B)

print(f"A 평균 효과: {mean_A}")
print(f"B 평균 효과: {mean_B}")
print(f"t-검정 통계량: {t_stat}")
print(f"p-값: {p_value}")

# t-검정의 p-값 확인 (위 예시에서 계산된 p-값 사용)
print(f"p-값: {p_value}")
if p_value < 0.05:
    print("귀무가설을 기각합니다. 통계적으로 유의미한 차이가 있습니다.")
else:
    print("귀무가설을 기각하지 않습니다. 통계적으로 유의미한 차이가 없습니다.")

3.3 t검정

가설검정의 대표적인 검정

t 검정 정의

• t검정은 두 집단 간의 평균 차이가 통계적으로 유의미한지 확인하는 검정 방법
• 독립표본 t검정과 대응표본 t검정으로 나뉨
• 독립표본 t검정 : 두 독립된 그룹의 평균을 비교
• 대응표본 t검정 : 동일한 그룹의 사전/사후 평균을 비교

실제 사례

• 두 클래스의 시험 성적 비교(독립표본 t검정)
• 다이어트 전후 체중 비교(대응표본 t검정)

< 코드 예시>

# 학생 점수 데이터
scores_method1 = np.random.normal(70, 10, 30)
scores_method2 = np.random.normal(75, 10, 30)

# 독립표본 t검정
t_stat, p_val = stats.ttest_ind(scores_method1, scores_method2)
print(f"T-Statistic: {t_stat}, P-value: {p_val}")

3.4 다중검정

여러 가설을 동시에 검정! 하지만 오류가 발생할 수 있음!

다중검정 정의 및 보정 방법

• 여러 가설을 동시에 검정할 때 발생하는 문제
• 각 검정마다 유의수준을 조정하지 않으면 1종 오류(귀무가설이 참인데 기각하는 오류) 발생 확률이 증가
  <보정 방법>
• 본페로니 보정, 튜키 보정, 던넷 보정, 윌리엄스 보정 등이 있음
• 가장 대표적이고 기본적인게 본페로니 보정

실제 사례

• 여러 약물의 효과를 동시에 검정 -> 이 때 본페로니 보정을 사용해볼 수 있음

<코드 예시>

import numpy as np
import scipy.stats as stats

# 세 그룹의 데이터 생성
np.random.seed(42)
group_A = np.random.normal(10, 2, 30)
group_B = np.random.normal(12, 2, 30)
group_C = np.random.normal(11, 2, 30)

# 세 그룹 간 평균 차이에 대한 t검정 수행
p_values = []
p_values.append(stats.ttest_ind(group_A, group_B).pvalue)
p_values.append(stats.ttest_ind(group_A, group_C).pvalue)
p_values.append(stats.ttest_ind(group_B, group_C).pvalue)

# 본페로니 보정 적용
alpha = 0.05
adjusted_alpha = alpha / len(p_values)

# 결과 출력
print(f"본페로니 보정된 유의 수준: {adjusted_alpha:.4f}")
for i, p in enumerate(p_values):
    if p < adjusted_alpha:
        print(f"검정 {i+1}: 유의미한 차이 발견 (p = {p:.4f})")
    else:
        print(f"검정 {i+1}: 유의미한 차이 없음 (p = {p:.4f})")

3.5 카이제곱검정

범주형 데이터의 분석에 사용한다는 것이 포인트!

카이제곱검정 정의

• 범주형 데이터의 표본 분포가 모집단 분포와 일치하는지 검정 (적합도 검정) 하거나
• 두 범주형 변수 간의 독립성을 검정 (독립성 검정)

적합도 검정

• 관찰된 분포와 기대된 분포가 일치하는지 검정
• p값이 높으면 데이터가 귀무 가설에 잘 맞음. 즉, 관찰된 데이터와 귀무 가설이 적합
• p값이 낮으면 데이터가 귀무 가설에 잘 맞지 않음. 즉, 관찰된 데이터와 귀무 가설이 부적합

독립성 검정

• 두 범주형 변수 간의 독립성을 검정
• p값이 높으면 두 변수 간의 관계가 연관성이 없음 → 독립성이 있음
• p값이 낮으면 두 변수 간의 관계가 연관성이 있음 → 독립성이 없음

실제 사례

🌞 범주형 데이터의 분포 확인 및 독립성 확인을 위해 사용

• 주사위의 각 면이 동일한 확률로 나오는지 검정(적합도 검정)
• 성별과 직업 만족도 간의 독립성 검정(독립성 검정)

<코드 예시>

# 적합도 검정
observed = [20, 30, 25, 25]
expected = [25, 25, 25, 25]
chi2_stat, p_value = stats.chisquare(observed, f_exp=expected)
print(f"적합도 검정 카이제곱 통계량: {chi2_stat}, p-값: {p_value}")

# 독립성 검정
observed = np.array([[10, 10, 20], [20, 20, 40]])
chi2_stat, p_value, dof, expected = stats.chi2_contingency(observed)
print(f"독립성 검정 카이제곱 통계량: {chi2_stat}, p-값: {p_value}")

# 성별과 흡연 여부 독립성 검정
observed = np.array([[30, 10], [20, 40]])
chi2_stat, p_value, dof, expected = stats.chi2_contingency(observed)
print(f"독립성 검정 카이제곱 통계량: {chi2_stat}, p-값: {p_value}")

<코드 설명>

• stats.chisquare 함수
  • scipy.stats.chisquare 함수는 카이제곱 적합도 검정을 수행하여 관찰된 빈도 분포가 기대된 빈도 분포와 일치하는지 평가
    이 검정은 주로 단일 표본에 대해 관찰된 빈도가 특정 이론적 분포(예: 균등 분포)와 일치하는지 확인하는 데 사용됨
  • 반환 값
    • chi2: 카이제곱 통계량
    • p: p-값, 이는 관찰된 데이터가 귀무 가설 하에서 발생할 확률
• ❓ stats.chi2_contingency 함수
  • scipy.stats.chi2_contingency 함수는 카이제곱 검정을 수행하여 두 개 이상의 범주형 변수 간의 독립성을 검정
    이 함수는 관측 빈도를 담고 있는 교차표(contingency table)를 입력으로 받아 카이제곱 통계량, p-값, 자유도, 그리고 기대 빈도(expected frequencies)를 반환
  • 반환 값
    • chi2 : 카이제곱 통계량
    • p : p-값, 이는 관측된 데이터가 귀무 가설 하에서 발생할 확률
    • dof : 자유도, 이는 (행의 수 - 1) * (열의 수 - 1)로 계산됨
    • expected : 기대 빈도, 이는 행 합계와 열 합계를 사용하여 계산된 이론적 빈도

3.6 제 1종 오류와 제 2종 오류

두가지의 오류를 구분하는 것이 포인트!

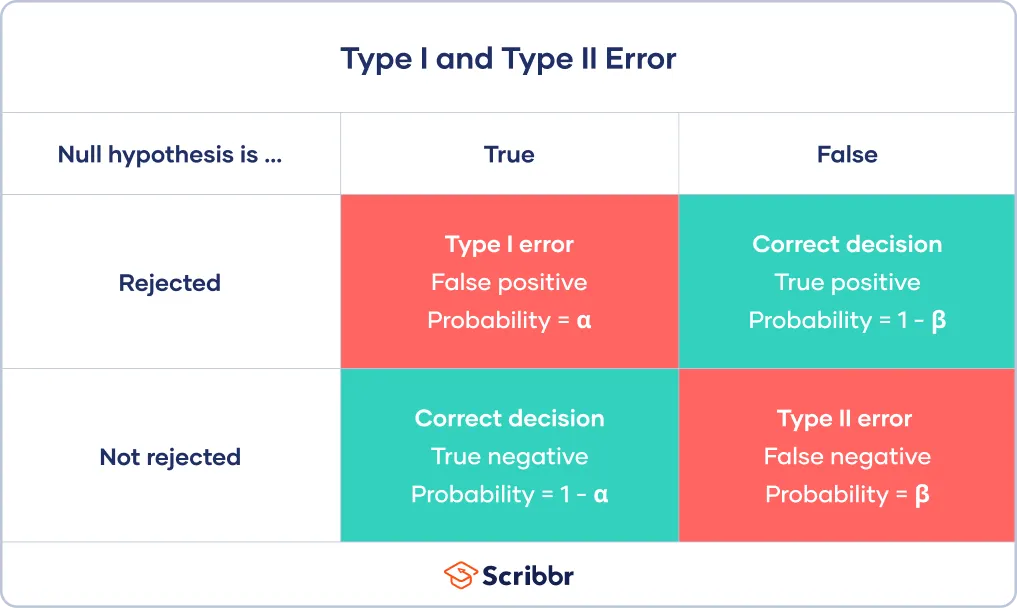
제 1종 오류

• 귀무가설이 참인데 기각하는 오류
• 잘못된 긍정을 의미 (아무런 영향이 없는데 영향이 있다고 하는 것)
• 한 단어로 위양성!
• α를 경계로 귀무가설을 기각하기 때문에 제1종 오류가 α만큼 발생
• 따라서 유의수준(α)을 정함으로써 제 1종 오류 제어 가능
• 만약, 유의수준이 0.05라면 100번 중 5번 정도 일어날 수 있는 제 1종 오류는 감수하겠다는 것
• 다중 검정시 제 1종 오류가 증가하는 이유?
  • 하나의 검정에서 제1종 오류가 발생하지 않을 확률은 $1-\alpha$
  • m개의 독립된 검정에서 제1종 오류가 전혀 발생하지 않을 확률은 $(1-\alpha)^{m}$
  • 따라서, m개의 검정에서 하나 이상의 제1종 오류가 발생할 확률(즉, 전체 제1종 오류율)은 $1-(1-\alpha)^{m}$
  • 이 값은 m이 커질수록 빠르게 증가함 -> 예를 들어, α=0.05, m=10인 경우 $1-(1-0.05)^{10} \approx 0.401$
  • 즉, 10개의 가설을 동시에 검정할 때 하나 이상의 가설에서 제 1종 오류가 발생할 확률이 약 40.1% 이므로 개별검증에서 발생하는 오류율(5%)보다 높음

제 2종 오류

• 귀무가설이 거짓인데 기각하지 않는 오류
• 잘못된 부정을 의미 (영향이 있는데 영향이 없다고 하는 것)
• 한 단어로 위음성!
• 제 2종 오류가 일어날 확률은 β로 정의
• 제 2종 오류가 일어나지 않을 확률은 검정력(1-β)으로 정의
• 하지만 이를 직접 통제할 수는 없음
• 그나마 통제를 해볼 수 있는 방법으로는…
  • 표본크기 n이 커질 수록 β가 작아짐.
  • α와 β는 상충관계에 있어서 너무 낮은 α를 가지게 되면 β는 더욱 높아짐

실제 사례

• 새로운 약물이 효과가 없는데 있다고 결론 내리는 것 (제 1종 오류)
• 효과가 있는데 없다고 결론 내리는 것 (제 2종 오류)

04.회귀

회귀분석 요약 (추가)

4.1 단순선형회귀

한개의 변수에 의한 결과를 예측

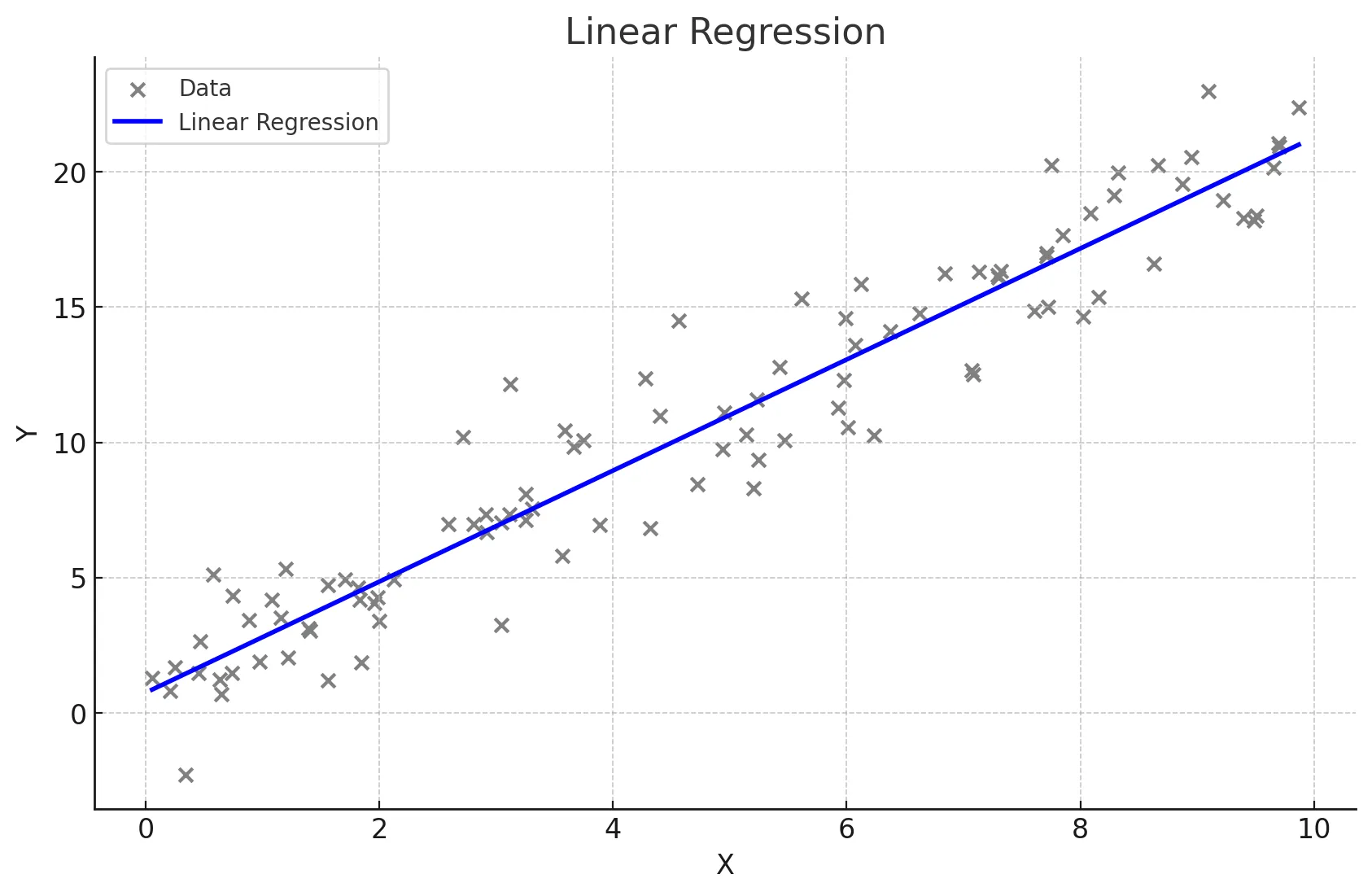
단순선형회귀 정의

• 하나의 독립 변수(X)와 하나의 종속 변수(Y) 간의 관계를 직선으로 모델링하는 방법
• 회귀식
  • Y = β0 + β1X, 여기서 β0는 절편, β1는 기울기
  • 중학교 때 배웠던 1차함수를 생각하면 이해하기 쉬움!
• 특징
  • 독립 변수의 변화에 따라 종속 변수가 어떻게 변화하는지 설명하고 예측
  • 데이터가 직선적 경향을 따를 때 사용함
  • 간단하고 해석이 용이
  • 데이터가 선형적이지 않을 경우 적합하지 않음

실제 사례

하나의 독립변수와 종속변수와의 관계를 분석 및 예측

• 광고비(X)와 매출(Y) 간의 관계 분석
• 현재의 광고비를 바탕으로 예상되는 매출을 예측 가능

<코드 예시>

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score

# 예시 데이터 생성
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

# 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 단순선형회귀 모델 생성 및 훈련
model = LinearRegression()
model.fit(X_train, y_train)

# 예측
y_pred = model.predict(X_test)

# 회귀 계수 및 절편 출력
print("회귀 계수:", model.coef_)
print("절편:", model.intercept_)

# 모델 평가
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print("평균 제곱 오차(MSE):", mse)
print("결정 계수(R2):", r2)

# 시각화
plt.scatter(X, y, color='blue')
plt.plot(X_test, y_pred, color='red', linewidth=2)
plt.title('linear regeression')
plt.xlabel('X : cost')
plt.ylabel('Y : sales')
plt.show()

4.2 다중선형회귀

두 개 이상의 변수에 의한 결과를 예측

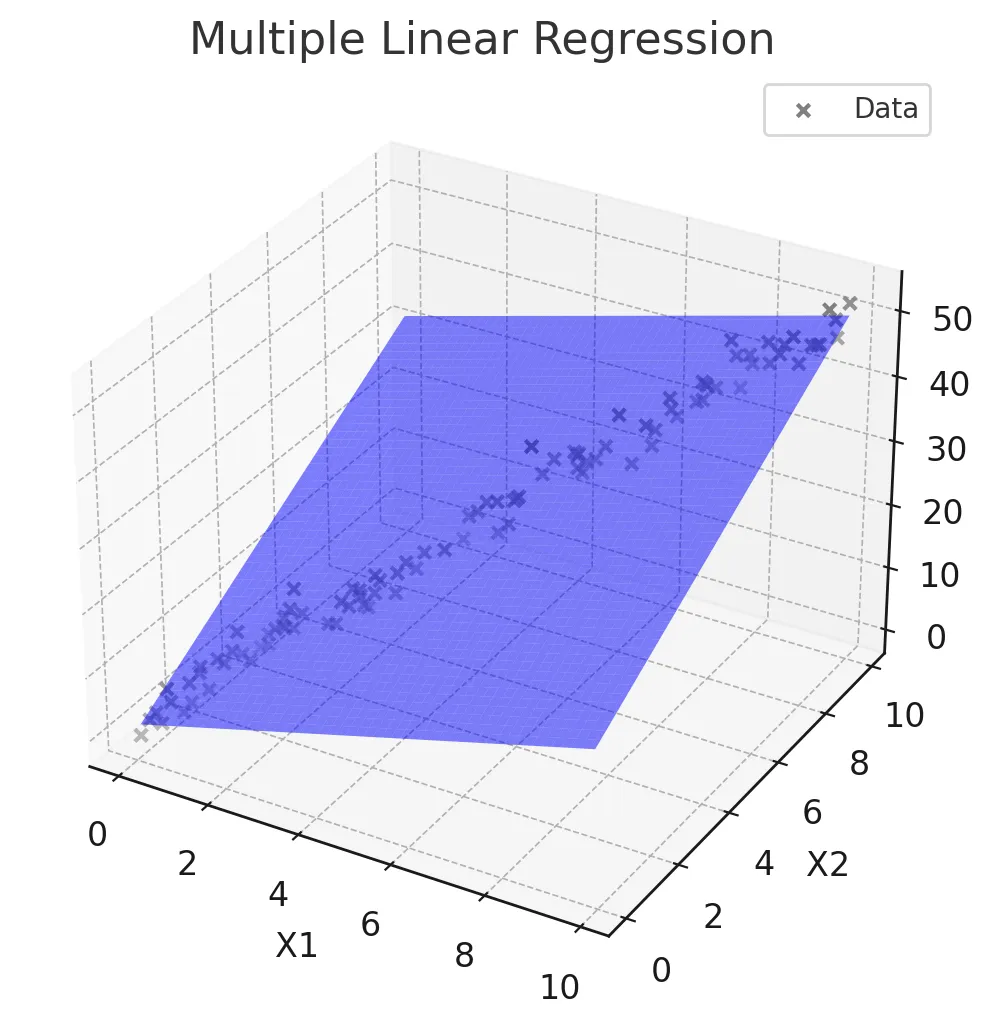
다중선형회귀 정의

• 두 개 이상의 독립 변수(X1, X2, ..., Xn)와 하나의 종속 변수(Y) 간의 관계를 모델링
• 회귀식
  • Y = β0 + β1X1 + β2X2 + ... + βnXn
• 특징
  • 여러 독립 변수의 변화를 고려하여 종속 변수를 설명하고 예측
  • 종속변수에 영향을 미치는 여러 독립변수가 있을 때 사용
  • 여러 변수의 영향을 동시에 분석할 수 있음
  • 변수들 간의 다중공선성 문제가 발생할 수 있음

✋🏻 다중공선성이란?

• 다중공선성(Multicollinearity)은 회귀분석에서 독립 변수들 간에 높은 상관관계가 있는 경우를 말함
• 이는 회귀분석 모델의 성능과 해석에 여러 가지 문제를 일으킬 수 있음
  • 독립 변수들이 서로 강하게 상관되어 있으면, 각 변수의 개별적인 효과를 분리해내기 어려워져 회귀의 해석을 어렵게 만들어버림
  • 다중공선성으로 인해 실제로 중요한 변수가 통계적으로 유의하지 않게 나타날 수 있음
• 진단 하는 법
  • 가장 간단한 방법으로는 상관계수를 계산하여 상관계수가 높은(약 0.7) 변수들이 있는지 확인
  • 더 정확한 방법으로는 분산 팽창 계수 (VIF)를 계산하여 VIF값이 10이 높은지 확인하는 방법으로 다중공선성이 높다고 판단
• 다중공선성 해결 방법
  • 가장 간단한 방법으로는 높은 계수를 가진 변수 중 하나를 제거
  • 혹은 주성분 분석(PCA)과 같은 변수들을 효과적으로 줄이는 차원 분석 방법을 적용하여 해결할 수도 있음

실제 사례

🫡 두 개 이상의 독립 변수와 종속변수와의 관계를 분석 및 예측

• 다양한 광고비(TV, Radio, Newspaper)과 매출 간의 관계 분석
• 현재의 광고비(TV, Radio, Newspaper)를 바탕으로 예상되는 매출을 예측 가능

<코드 예시>

# 예시 데이터 생성
data = {'TV': np.random.rand(100) * 100,
        'Radio': np.random.rand(100) * 50,
        'Newspaper': np.random.rand(100) * 30,
        'Sales': np.random.rand(100) * 100}
df = pd.DataFrame(data)

# 독립 변수(X)와 종속 변수(Y) 설정
X = df[['TV', 'Radio', 'Newspaper']]
y = df['Sales']

# 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 다중선형회귀 모델 생성 및 훈련
model = LinearRegression()
model.fit(X_train, y_train)

# 예측
y_pred = model.predict(X_test)

# 회귀 계수 및 절편 출력
print("회귀 계수:", model.coef_)
print("절편:", model.intercept_)

# 모델 평가
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print("평균 제곱 오차(MSE):", mse)
print("결정 계수(R2):", r2)

4.3 범주형 변수

회귀에서 범주형 변수의 경우 특별히 변환을 해주어야 함!

범주형 변수 종류

1. 순서가 있는 범주형 변수 : 옷의 사이즈 (L, M, …), 수능 등급 (1등급, 2등급, ….)과 같이 범주형 변수라도 순서가 있는 변수
   -> 이런 경우 각 문자를 임의의 숫자로 변환해도 문제 없음 (순서가 잘 반영될 수 있게 숫자로 변환)
   ex) XL → 3, L → 2, M → 1, S → 0
2. 순서가 없는 범주형 변수 : 성별 (남,여), 지역 (부산, 대구, 대전, …) 과 같이 순서가 없는 변수

실제 사례

🌸 범주형 변수를 찾고 더미 변수로 변환한 후 회귀 분석 수행

<순서>

• 성별, 근무 경력과 연봉 간의 관계.
• 성별과 근무 경력이라는 요인변수 중 성별이 범주형 요인변수에 해당
• 해당 변수를 더미 변수로 변환
• 회귀 수행

<코드 예시>

# 예시 데이터 생성
data = {'Gender': ['Male', 'Female', 'Female', 'Male', 'Male'],
        'Experience': [5, 7, 10, 3, 8],
        'Salary': [50, 60, 65, 40, 55]}
df = pd.DataFrame(data)

# 범주형 변수 더미 변수로 변환
df = pd.get_dummies(df, drop_first=True)

# 독립 변수(X)와 종속 변수(Y) 설정
X = df[['Experience', 'Gender_Male']]
y = df['Salary']

# 단순선형회귀 모델 생성 및 훈련
model = LinearRegression()
model.fit(X, y)

# 예측
y_pred = model.predict(X)

# 회귀 계수 및 절편 출력
print("회귀 계수:", model.coef_)
print("절편:", model.intercept_)

# 모델 평가
mse = mean_squared_error(y, y_pred)
r2 = r2_score(y, y_pred)
print("평균 제곱 오차(MSE):", mse)
print("결정 계수(R2):", r2)

4.4 다항회귀, 스플라인 회귀

데이터가 훨씬 복잡할 때 사용하는 회귀

다항회귀, 스플라인 회귀란?

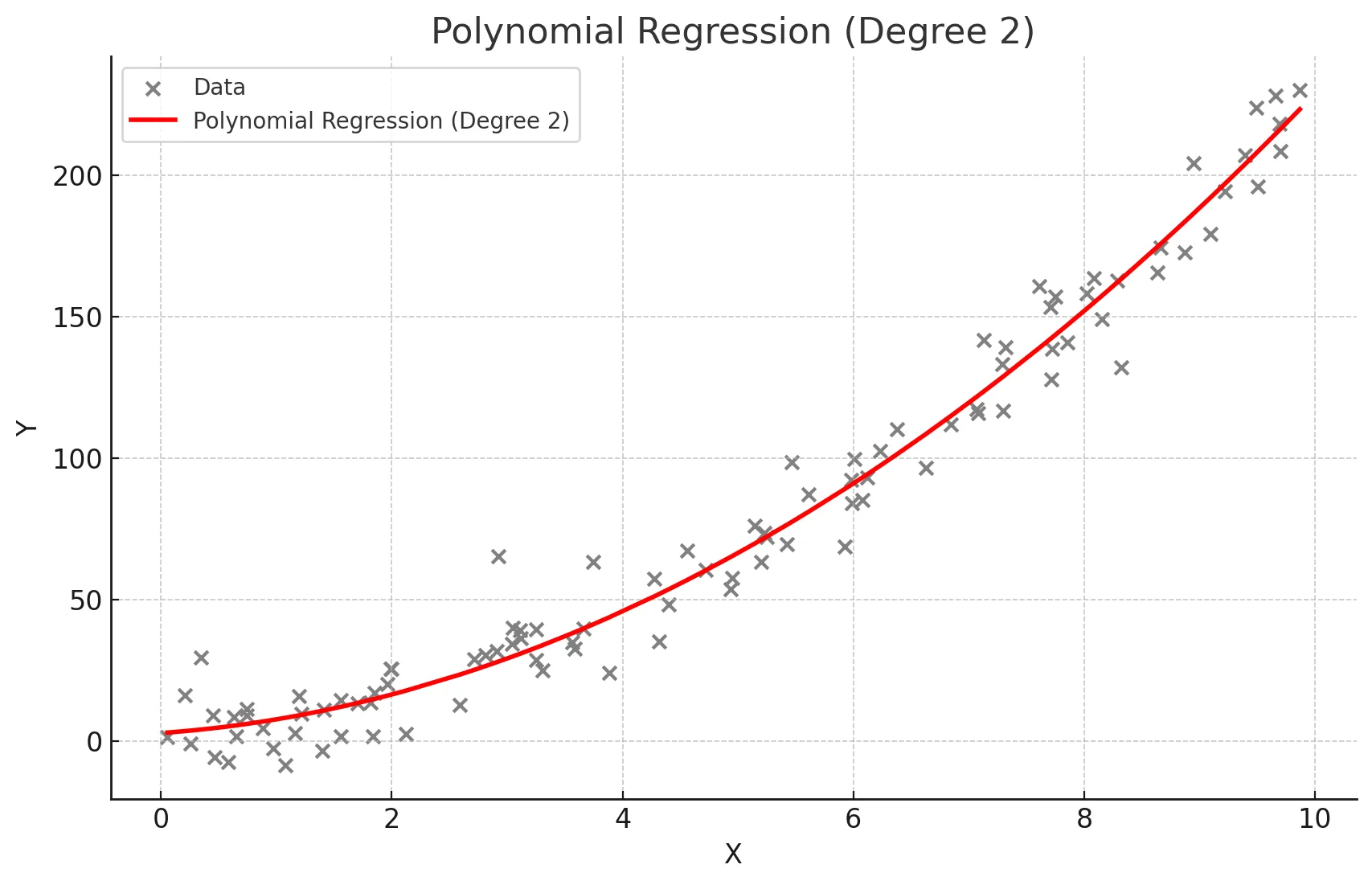
☑️ 다항회귀

• 독립 변수와 종속 변수 간의 관계가 선형이 아닐 때 사용 -> 독립 변수의 다항식을 사용하여 종속 변수를 예측
• 데이터가 곡선적 경향을 따를 때 사용
• 비선형 관계를 모델링할 수 있음
• 고차 다항식의 경우 과적합(overfitting) 위험이 있음
  

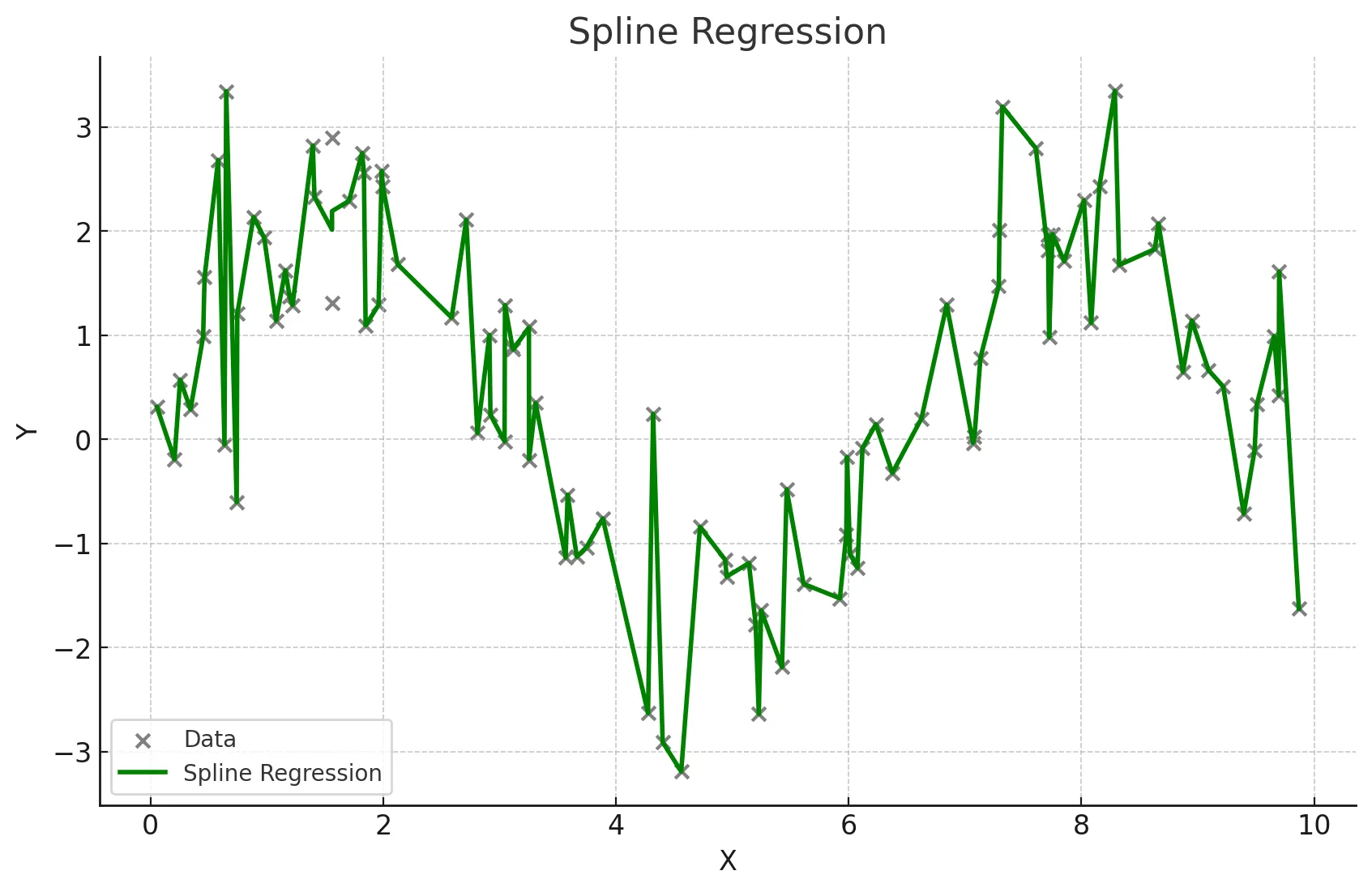
☑️ 스플라인 회귀

• 독립 변수의 구간별로 다른 회귀식을 적용하여 복잡한 관계를 모델링
• 구간마다 다른 다항식을 사용하여 전체적으로 매끄러운 곡선을 생성
• 데이터가 국부적으로 다른 패턴을 보일 때 사용
• 복잡한 비선형 관계를 유연하게 모델링할 수 있음
• 적절한 매듭점(knots)의 선택이 중요
  

다항 회귀 실제 사례

독립변수와 종속변수의 관계가 비선형 관계일 때 사용

• 주택 가격 예측(면적과 가격 간의 비선형 관계)

from sklearn.preprocessing import PolynomialFeatures

# 예시 데이터 생성
np.random.seed(0)
X = 2 - 3 * np.random.normal(0, 1, 100)
y = X - 2 * (X ** 2) + np.random.normal(-3, 3, 100)
X = X[:, np.newaxis]

# 다항 회귀 (2차)
polynomial_features = PolynomialFeatures(degree=2)
X_poly = polynomial_features.fit_transform(X)

model = LinearRegression()
model.fit(X_poly, y)
y_poly_pred = model.predict(X_poly)

# 모델 평가
mse = mean_squared_error(y, y_poly_pred)
r2 = r2_score(y, y_poly_pred)
print("평균 제곱 오차(MSE):", mse)
print("결정 계수(R2):", r2)

# 시각화
plt.scatter(X, y, s=10)
# 정렬된 X 값에 따른 y 값 예측
sorted_zip = sorted(zip(X, y_poly_pred))
X, y_poly_pred = zip(*sorted_zip)
plt.plot(X, y_poly_pred, color='m')
plt.title('polynomial regerssion')
plt.xlabel('area')
plt.ylabel('price')
plt.show()

선형회귀, 로지스틱회귀 정리(추가)

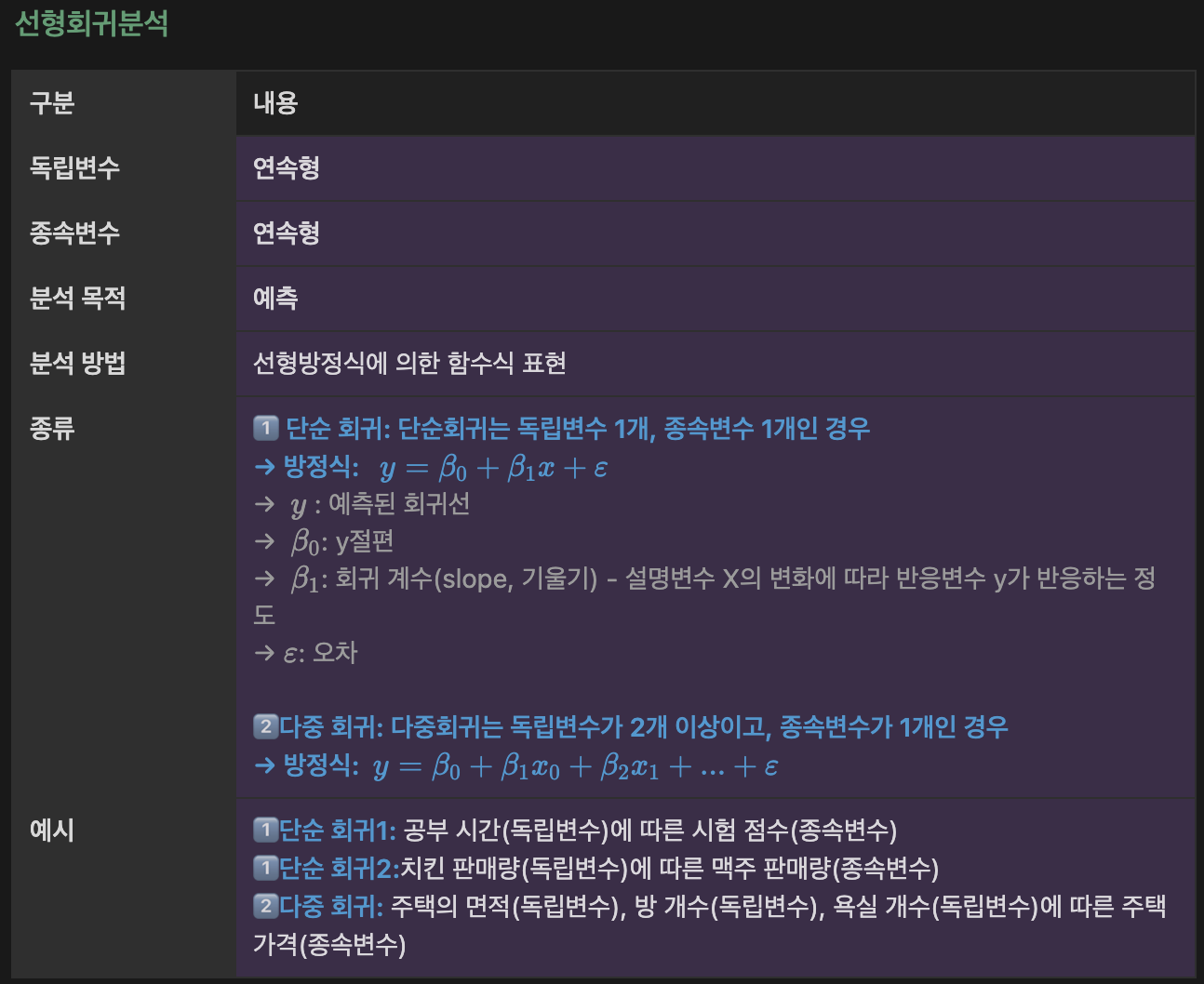
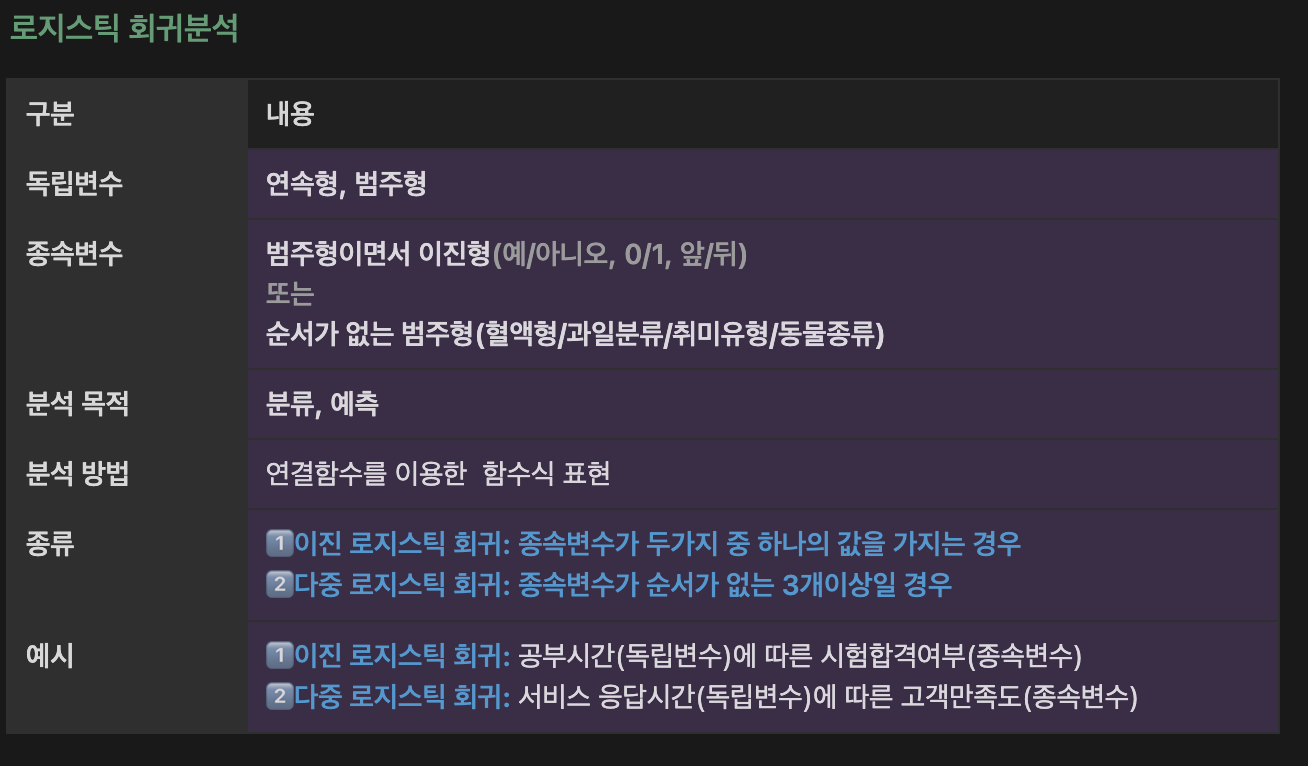
정합성 검증 & 결과 해석(추가)

1️⃣ 회귀모델(회귀식)이 얼마나 설명력을 갖는지? 

-> 결정계수 R_squared(R²) 를 확인

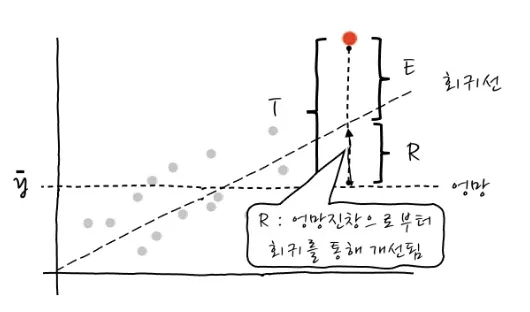
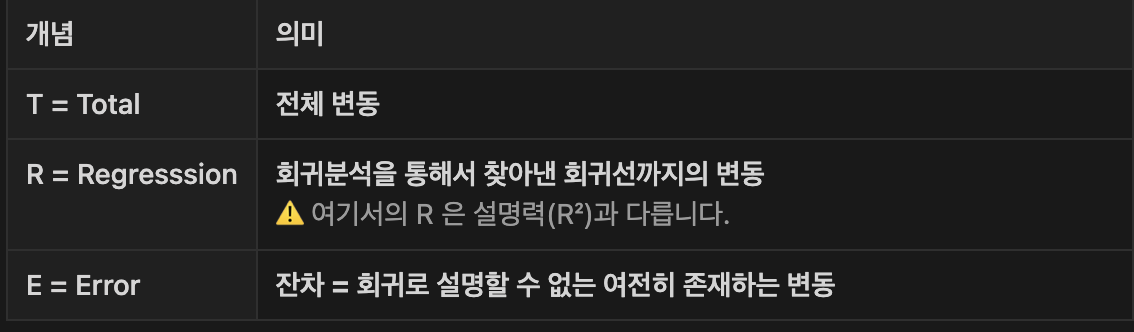
설명력(R²)은 전체오류중 회귀를 함으로써 얼마나 개선되었는가를 의미
-> 설명력은 0과 1 사이의 값을 가지며, 1에 가까울수록 모델의 성능이 좋다는 것을 의미

2️⃣ 회귀모델(회귀식)이 통계적으로 유의한지?

-> 회귀식에 대한 F검정 시행

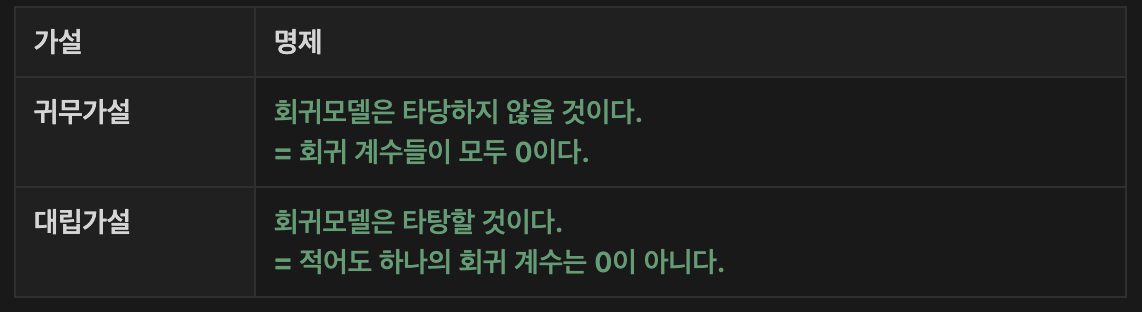
→ p-value로 유의성을 판단

→ F-검정을 통해 얻은 p-value 값이 0.05보다 작다면 대립가설을 채택(신뢰도95%)

3️⃣ 독립변수와 종속변수 간 선형관계가 있는지?

-> 회귀식의 $\beta_1$(기울기) 에 대한 t 검정 시행

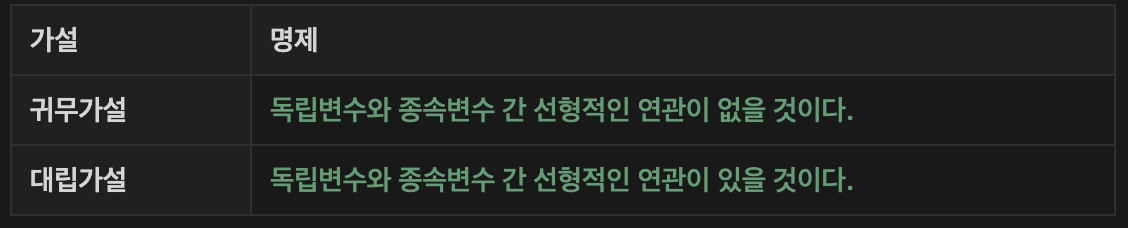
-> p-value로 유의성을 판단

-> t-검정을 통해 얻은 p-value 값이 0.05보다 작다면 대립가설을 채택

4️⃣ OLS(Ordinary Least Squares) 해석하기

OLS = 선형 회귀 모델의 결과를 나타내는 회귀 결과 표
summary 라는 함수를 통해 아래와 같은 결과표를 얻을 수 있음

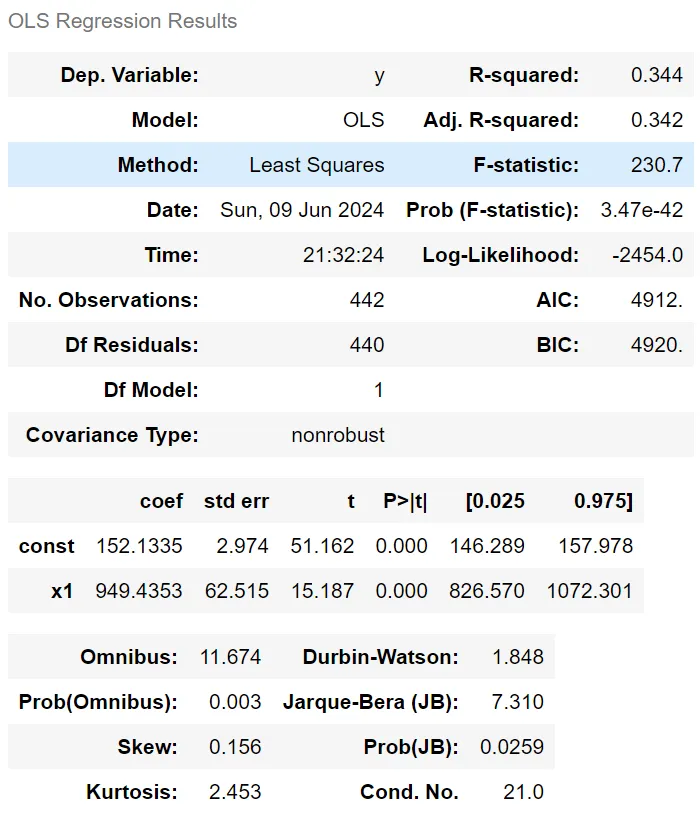
• 주요 지표 총정리

1. Dep. Variable (y): 종속 변수
2. R-squared (0.344): 결정계수로, 회귀 모델이 종속 변수의 변동성을 얼마나 설명하는지를 나타냄
   -> 이 값은 0에서 1 사이에 위치하며, 0.344는 약 34.4%의 변동성이 설명된다는 것을 의미
3. Adj. R-squared (0.342): 수정된 결정계수로, 설명 변수의 개수를 고려하여 R-squared 값을 조정한 것
   -> 변수의 수가 늘어날 때 발생하는 과적합을 방지하기 위해 사용됨
   -> 0.342는 모델이 적절하게 조정되었음을 나타냅니다.
4. Method (Least Squares): 사용된 회귀 방법이 최소제곱법임을 나타냄
   1. 최소제곱법: 근사적으로 구하려는 해와 실제 해의 오차의 제곱의 합이 최소가 되는 해를 구하는 방법
5. F-statistic (230.7): 회귀 모형의 전체 유의성을 검정하는 F-통계량입니다. 값이 클수록 모형이 유의미할 가능성이 높음
6. Prob (F-statistic) (3.47e-42): F-통계량의 p-값으로, 이 값이 매우 작으면 대립가설을 채택할 수 있음 -> 이 경우 p-값이 거의 0에 가까우므로, 회귀 모형이 통계적으로 유의미하다고 볼 수 있음
7. Log-Likelihood (-2454.0): 회귀 모형의 로그 우도(likelihood) -> 값이 클수록 모형이 데이터에 더 잘 맞는다는 것을 의미
8. No. Observations (442): 사용된 관측치(데이터 포인트)의 수
9. Df Residuals (440): 잔차의 자유도, 즉 전체 데이터 포인트 수에서 회귀 계수의 수를 뺀 값
10. Df Model (1): 모델에 포함된 설명 변수의 수
11. Covariance Type (nonrobust): 공분산 추정의 유형을 나타냄 nonrobust는 기본 공분산 추정이 사용되었음을 의미
12. coef (coefficients):
    • const (152.1335): 상수항(절편)으로, 독립변수가 0일 때 종속 변수의 예측값
    • x1 (949.4353): 설명 변수 x1의 회귀 계수로, 독립변수가 1 단위 증가할 때 종속 변수가 평균적으로 949.4353 단위 증가한다는 의미
13. std err (Standard Error): 회귀 계수 추정치의 표준 오차입니다. 상수항과 x1에 각각 2.974, 62.515가 있음
14. t (t-statistic): 회귀 계수가 0인지 검정하는 t-값
    -> 절대값이 클수록 해당 계수가 유의미할 가능성이 높음
    -> x1의 t-값은 15.187로 매우 크며 유의미함을 나타냄
15. P>|t| (P-value): 각 계수에 대한 p-값
    -> 일반적으로 0.05보다 작으면 해당 계수는 유의미하다고 판단
    -> x1과 상수항의 p-값은 모두 0으로, 매우 유의미
16. [0.025 0.975] (Confidence Interval): 회귀 계수에 대한 95% 신뢰구간입니다.
    예를 들어, x1의 신뢰구간은 [826.570, 1072.301]로,
    -> 이 범위 내에서 실제 계수가 있을 가능성이 95%
17. Omnibus (11.674): 잔차의 정규성을 검정하는 Omnibus 검정 통계량
    -> 값이 작을수록 잔차가 정규분포에 가깝다는 의미
18. Prob(Omnibus) (0.003): Omnibus 검정의 p-값
    -> 0.05보다 작으므로 잔차가 정규분포에서 벗어날 가능성이 있음
19. Skew (0.156): 잔차의 왜도(skewness)
    -> 값이 0에 가까울수록 대칭적
20. Kurtosis (2.453): 잔차의 첨도(kurtosis)
    -> 3에 가까울수록 정규분포에 가까움
    -> 2.453은 정규분포보다 조금 더 평평함을 의미
21. Durbin-Watson (1.848): 잔차의 자기상관을 검정하는 통계량
    -> 2에 가까우면 자기상관이 없음을 의미
22. Jarque-Bera (JB) (7.310): 잔차의 정규성을 검정하는 Jarque-Bera 검정 통계량
23. Prob(JB) (0.0259): Jarque-Bera 검정의 p-값
    -> 0.05보다 작아 잔차가 정규성을 만족하지 않을 가능성이 있음
24. Cond. No. (21.0): 설명 변수의 다중공선성을 나타내는 조건수
    -> 값이 높으면 다중공선성 문제가 있음을 시사