AIFFEL FD #20 활성화 함수 (Activation Function)

✅ 핵심내용

• 신경세포, 퍼셉트론의 구조
• 선형과 비선형
• 활성화 함수의 종류 (이진 계단 함수, 선형 활성화 함수, 비선형 활성화 함수)

---

퍼셉트론

딥러닝 모델은 보통 여러 개의 층으로 이루어져 있다. 그중에 하나의 층을 가져와 다시 쪼갠다면 보통 '노드'라고 불리는 것으로 쪼개지게 되는데, 이것이 바로 퍼셉트론(Perceptron)이다.

퍼셉트론은 동물의 신경세포와 유사하게 설계해나오게 되었다. 신경세포의 구조와 퍼셉트론의 구조를 비교해가며 살펴보자.

신경세포의 구조

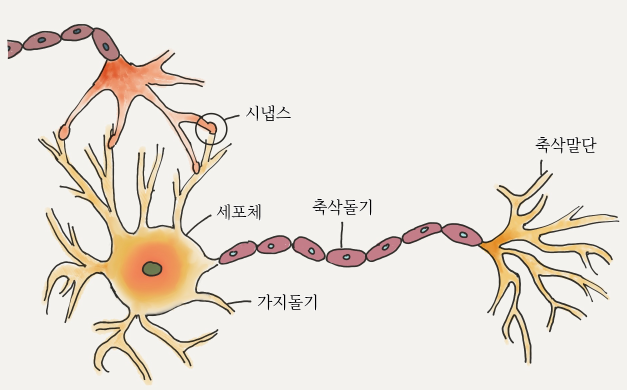
• 가지돌기 : 세포로 전달되는 신호를 받아들임

• 축삭돌기 : 세포에서 다른 세포로 신호를 전달하는 부분

• 시냅스

  • 가지돌기와 축삭돌기 사이에 있는 부분으로 신호 전달의 세기를 담당하며 시냅스의 발달 정도에 따라 같은 신호도 강하게 전달되거나 약하게 전달됨
  • 시냅스는 사용 빈도에 따라 커지거나 작아지며 심지어 시냅스 자체가 사라지기도 함

• 세포체

  • 각 가지돌기로부터 들어온 신호들로부터 자신의 출력 신호를 만들고 이를 다음 세포에 전송
  • 이때, 출력 신호는 단순히 입력신호들의 합이 아닌 비선형 방식으로 결정됨
  • 합이 일정 수준 이하이면 비활성 상태가 되어 신호를 무시하고, 일정 수준을 넘게 되면 활성 상태가 되어 신호를 다음 세포로 전송함

퍼셉트론의 구조

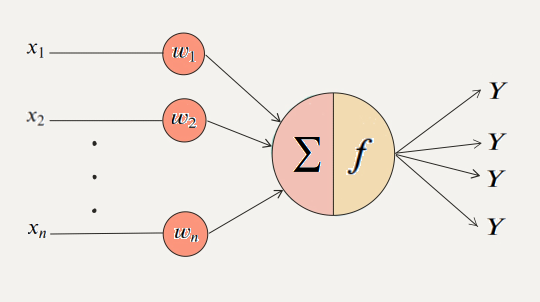
• 퍼셉트론에 주어지는 입력 ($x_1,x_2,..x_n$) : 신경세포에서 가지돌기로 받아들이는 신호

• 각 입력 항에 곱해지는 가중치 : 신경 세포들의 연결 부위에 형성된 시냅스의 발달 정도

• $x_iw_i$ 값들과 추가로 편향($b$)가 합쳐짐

• 활성화 함수(activation function : 세포체에서 신호를 처리하는 방식

• 활성화 함수를 거쳐 출력($Y$)이 결정됨

• 퍼셉트론과 신경세포 비교

퍼셉트론(노드)	신경세포(뉴런)
입력 신호($x_1,x_2,..x_n$)	가지돌기
출력 신호($Y$)	축삭돌기
가중치($w_1,w_2,..w_n$)	시냅스
활성화 함수	세포 활성화

---

활성화 함수

활성화 함수는 신경 세포로 치면 세포체에서 하는 일을 수행한다. 들어온 신호가 특정 임계점을 넘으면 출력을 하고, 넘지 못하면 무시를 한다.

활성화 함수는 신호를 전달 해주기 때문에 Transfer function 으로도 알려져있다.

활성화 함수는 크게

• 선형 활성화 함수(Linear activation function)
• 비선형 활성화 함수(Non-Linear activation function)
  으로 나눌 수 있는데 딥러닝에서는 일반적으로 비선형 활성화 함수를 사용한다.

왜일까? 이를 알아보기위해 선형과 비선형에 대해 알아보자.

---

선형과 비선형

선형

선형 변환은 선형 이라는 규칙을 지키면 $V$ 공간상의 벡터를 $W$ 공간상의 벡터로 바꿔주는 역할을 한다.

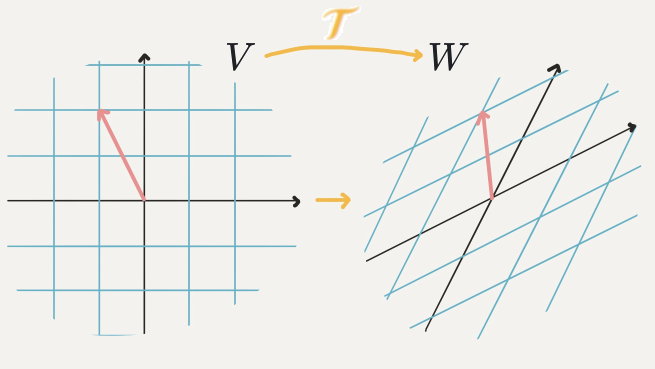
선형 변환의 정의
$V$ 와 $W$ 가 어떤 벡터 공간이고 둘 모두 실수 집합에 있다고 가정할 때 함수 $\mathcal{T}: V \rightarrow W$ 가 다음 두 조건을 만족할 때,

• 가산성(Additivity) : 모든 $x, y \in V$ 에 대해, $\mathcal{T}(x+y) = \mathcal{T}(x)+ \mathcal{T}(y)$
• 동차성(Homogeneity) :모든 $x \in V, c \in \Bbb{R}$ 에 대해, $\mathcal{T}(cx) = c\mathcal{T}(x)$
  함수 $\mathcal{T}$ 를 선형 변환(linear transformation) 이라고 한다.

비선형

딥러닝에서는 모델의 표현력을 향상시키기 위해 비선형 활성화 함수를 사용한다. 그 이유는 아래와 같다.

• 선형함수끼리의 합성함수도 선형함수이기 때문에 활성화 함수로 선형 함수를 쓰면 다층 신경망을 구성하는 이유가 없음 (결국은 하나의 선형함수로 표현 가능하기 때문)
• 즉, 선형 활성화 함수를 사용한다면, 노드의 개수를 아무리 많이 붙여도 결국 하나의 노드를 사용하는 것과 차이가 없음

---

활성화 함수의 종류

활성화 함수는 크게 3가지 종류의 함수로 나눌 수 있다.

• 이진 계단 함수(Binary step function)
• 선형 활성화 함수(Linear activation function)
• 비선형 활성화 함수(Non-linear activation function)

이진 계단 함수(Binary step function)

이진 계단 함수(Binary step function)는 들어온 입력이 특정 임계점을 넘으면 1(혹은 True)를 출력하고 그렇지 않을 때는 0을 출력한다. 따라서 간단한 이진 분류 문제에서 유용하게 사용된다.

아래의 식은 임계점이 0일때의 이진 계단 함수식이다.

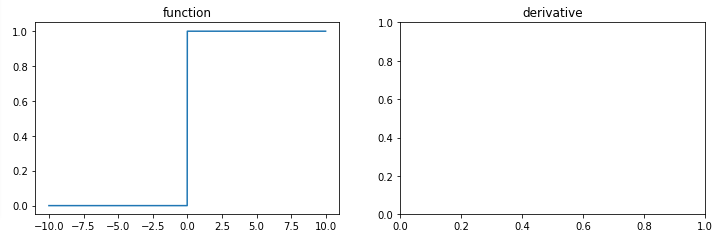
• 이진 계단 함수 특징

  • 이진 계단 함수는 단층 퍼셉트론(single layer perceptrons)라는 초기의 신경망에서 자주 사용되었음
  • 선형적으로 구분 가능한(linearly separable) 문제(ex, AND gate, OR gate) 구현 가능

• 이진 계단 함수 한계

  • 단층 퍼셉트론은 XOR gate 같은 그래프를 하나의 선으로 구분을 할 수 없는 경우를 구현 불가
  • 이를 해결할 방법이 여러 층을 쌓는 모델인 다층 퍼셉트론(multi-layer perceptron, MLP)
  • 역전파 알고리즘(backpropagation algorithm)을 사용하지 못함
  • 다중 출력이 불가능하여 다양한 클래스를 구분하는 문제 해결 불가

이진 계단 함수를 구현하고 특징과 한계를 시각화한 과정을 아래의 GitHub 링크에 기록하였다.

GitHub Link : Activation_Function

---

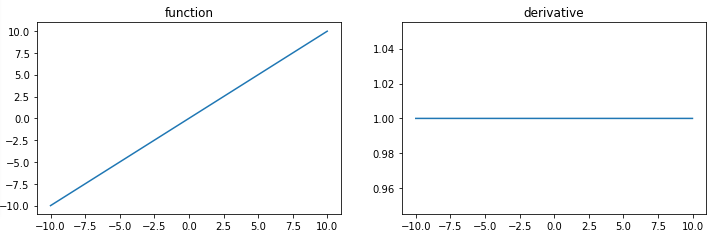
선형 활성화 함수

선형 활성화 함수(linear activation function)은 말 그대로 '선형'인 활성화 함수이다.

• 선형 활성화 함수 특징

  • 이진 계단 함수를 사용한 모델과 다르게 다중 출력이 가능
  • 이진 분류 문제와 간단한 다중 분류 문제까지도 해결 가능
  • 역전파 알고리즘 사용 가능

• 선형 활성화 함수 한계

  • XOR gate 같은 그래프를 하나의 선으로 구분을 할 수 없는 경우를 구현 불가
  • 즉, 비선형적 특성을 지닌 데이터를 예측하지 못함

선형 활성화 함수를 구현하고 특징과 한계를 시각화한 과정을 아래의 GitHub 링크에 기록하였다.

GitHub Link : Activation_Function

---

비선형 활성화 함수 - 시그모이드, Softmax

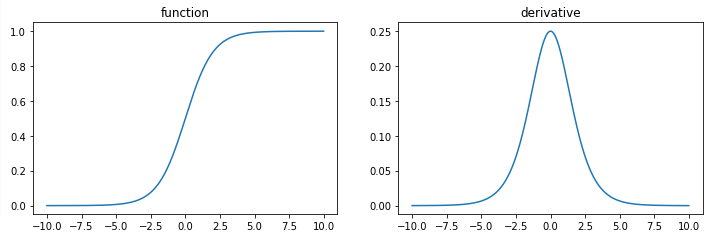
시그모이드, 로지스틱

시그모이드(sigmoid) 함수 (또는 logistic 함수)는 다음과 같이 표현된다.

$\sigma(x)=\frac{1}{1+e^{-x}}$

• 시그모이드 함수 특징

  • 시그모이드 함수의 치역은 (0,1), 즉, $0<\sigma(x)<1$
  • 따라서 확률을 예측해야하는 모델에서 자주 사용됨

• 시그모이드 함수 단점

  • 시그모이드 함수는 0 또는 1에서 포화(saturate) 됨
  • 입력값이 아무리 커져도 함수의 출력은 1에 가까워질 뿐 1 이상으로 높아지지 않고, 아무리 작아져도 출력은 0 이하로 떨어지지 않는다는 것
  • 그래디언트가 0과 아주 가까워져 가중치 업데이트가 일어나지 않게 됨
  • 훈련의 시간이 오래걸리게 됨

시그모이드 활성화 함수를 구현하고 특징과 한계를 시각화한 과정을 아래의 GitHub 링크에 기록하였다.

GitHub Link : Activation_Function

Softmax

Softmax 는 class의 수에 제한 없이 각 class의 확률을 구할 때 쓰인다.

• Softmax 함수 특징
  • 확률의 성질인 모든 경우의 수(=모든 class)의 확률을 더하면 1 이 됨
  • 보통 모델의 마지막 layer 에서 활용됨

---

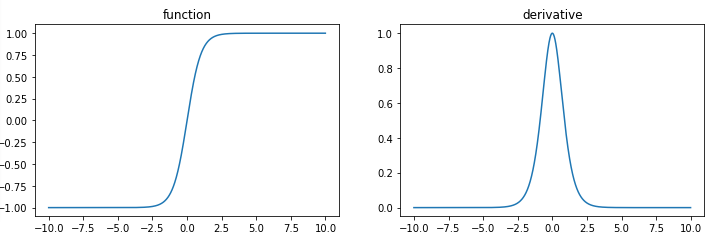
비선형 활성화 함수-하이퍼볼릭 탄젠트 ($tanh$)

하이퍼볼릭 탄젠트(tanh, Hyperbolic tangent) 함수는 쌍곡선 함수 중 하나로 다음과 같이 표현된다.

$\tanh (x)=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}$

• 하이퍼볼릭 탄젠트 함수 특징

  • 하이퍼볼릭 탄젠트 함수의 치역은 (-1,1), 즉, $-1<\sigma(x)<1$
  • 0을 중심으로 함
  • 일반적으로 하이퍼볼릭 탄젠트 함수를 사용한 모델이 시그모이드 함수를 사용한 모델보다 더 빨리 훈련됨

• 하이퍼볼릭 탄젠트 함수 단점

  • -1 또는 1에서 포화됨

하이퍼볼릭 탄젠트 함수를 구현하고 특징과 한계를 시각화한 과정을 아래의 GitHub 링크에 기록하였다.

GitHub Link : Activation_Function

---

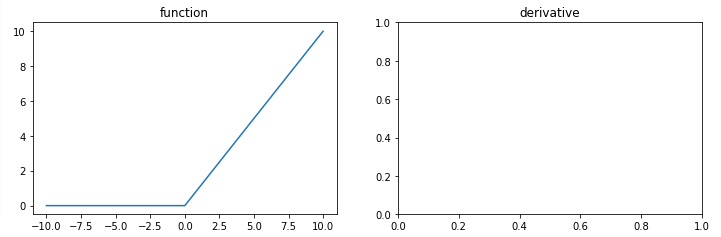
비선형 활성화 함수-ReLU

ReLU(rectified linear unit) 함수는 최근 가장 많이 사용되고 있는 활성화 함수이고 다음과 같이 표현된다.

$f(x)=\max (0, x)$

• ReLU 함수 특징

  • ReLU 함수의 치역은 $[0, \infty)$
  • 하이퍼볼릭 탄젠트를 사용한 모델보다 몇 배 더 빠르게 훈련됨

• ReLU 함수 단점

  • ReLU 함수의 출력값이 0 이 중심이 아님
  • Dying ReLU (모델에서 ReLU를 사용한 노드가 비활성화되며 출력을 00으로만 하게 되는 현상)
  • Dying ReLU는 학습률(learning rat)를 크게 잡을 때 자주 발생

ReLU 함수를 구현하고 특징과 한계를 시각화한 과정을 아래의 GitHub 링크에 기록하였다.

GitHub Link : Activation_Function

---

ReLU 의 단점을 극복하기 위한 시도

Leaky ReLU

Leaky ReLU함수는 ReLU 함수의 'Dying ReLU'를 해결하기 위한 시도 중 하나로 다음과 같이 표현한다.

• 'Dying ReLU'를 발생시켰던 0을 출력하던 부분을 아주 작은 음수값을 출력하게 만들어 주어 해당 문제를 해결

$f(x)=\max (0.01 x, x)$

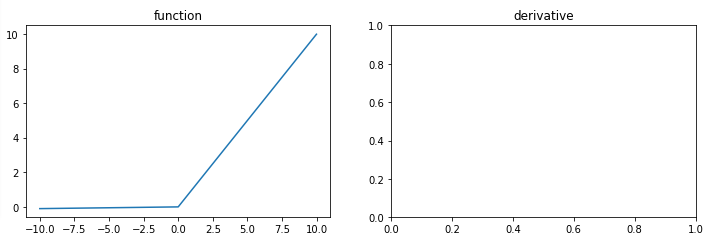
Leaky ReLU 함수를 구현하고 시각화한 과정을 아래의 GitHub 링크에 기록하였다.

GitHub Link : Activation_Function

PReLU

PReLU(parametric ReLU) 는 Leaky ReLU와 유사하지만 새로운 파라미터를 추가하여 0 미만일 때의 '기울기'가 훈련되게 했다.

$f(x)=\max (\alpha x, x)$
여기서 $\alpha$가 훈련과정에서 업데이트 된다.

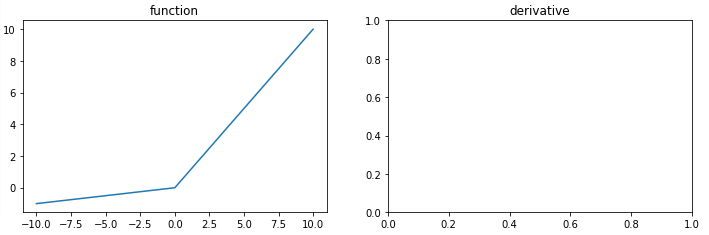
PReLU 함수를 구현하고 시각화한 과정을 아래의 GitHub 링크에 기록하였다.

GitHub Link : Activation_Function

ELU

ELU(exponential linear unit)은 ReLU의 모든 장점을 포함하며, 0이 중심점이 아니었던 단점과, 'Dying ReLU'문제를 해결한 활성화 함수이다.

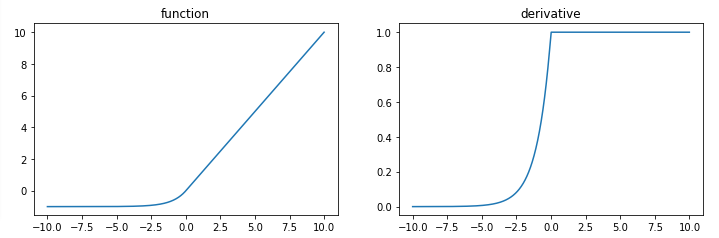
• ELU 함수 단점
  • exponential 연산이 들어가서 계산 비용이 높아짐

ELU 함수를 구현하고 시각화한 과정을 아래의 GitHub 링크에 기록하였다.

GitHub Link : Activation_Function