AI_Tech부스트캠프 week16...[4] Knowledge distillation(1)

Leejaegun·2024년 12월 26일

NaverAIBoostCamp

AI_tech_CV트랙 여정

목록 보기

63/74

1. Concept of Knowledge Distillation

1.1 What is Knowledge Distillation?

경량화의 한 종류로써, 고성능의 Teacher 모델로부터 지식을 전달 받아서 Student 모델을 학습 시키는 기법

1.2 KD Taxonomy

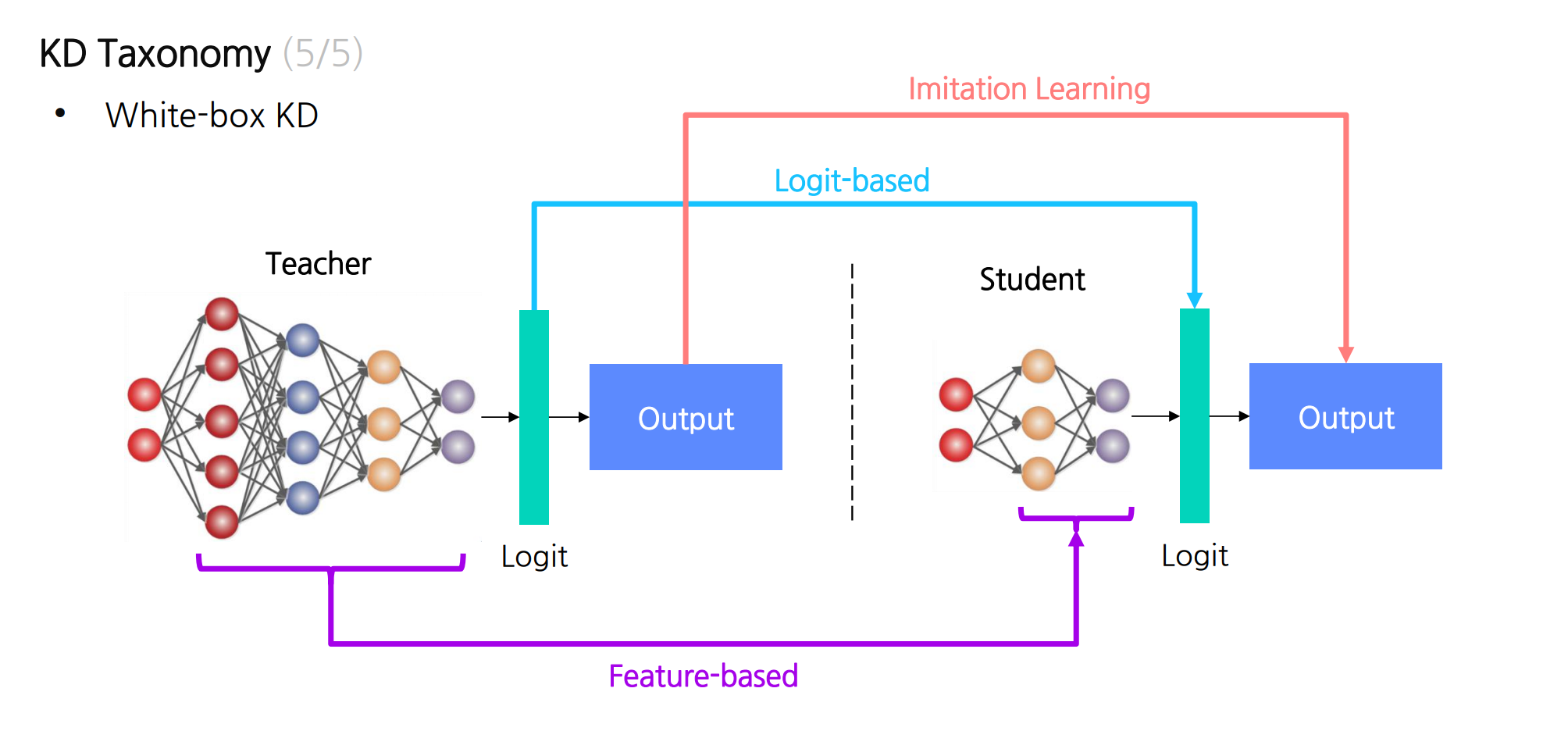
{"White-box KD" : Feature based,
"Gray-box KD": Logit-based,
"Black-box KD: Imitation-learning}

2. Logit-based KD

2.1 Logit-based

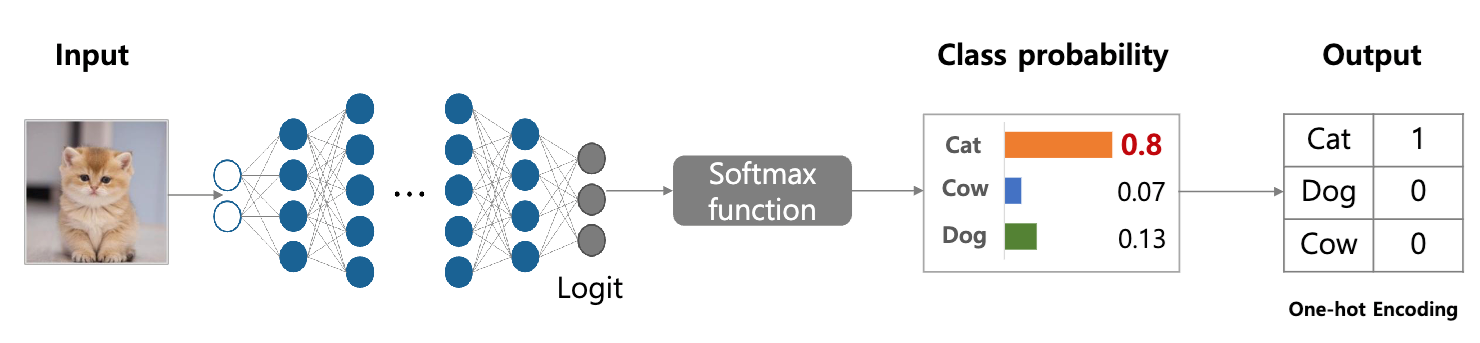
정답 학습과 더불어, 세부적인 선택지 간의 차이와 의미를 이해하도록 함.
Logit 값 안에는 정답 외에도 선택지 간의 상대적 가능성 및 유사도 정보가 들어 있음.

teacher model의 logit값을 지식으로 활용.-> teacher 의 지식값은 logit으로 계산된 클래스 확률값

클래스 간의 유사도 정보가 간접적으로 있기 때문에 teacher는 데이터를 학습하면서 클래스 간 유사도를 자연스럽게 파악
그리고 이는 유용한 지식이라는 가정을 하는 것.

Student의 학습

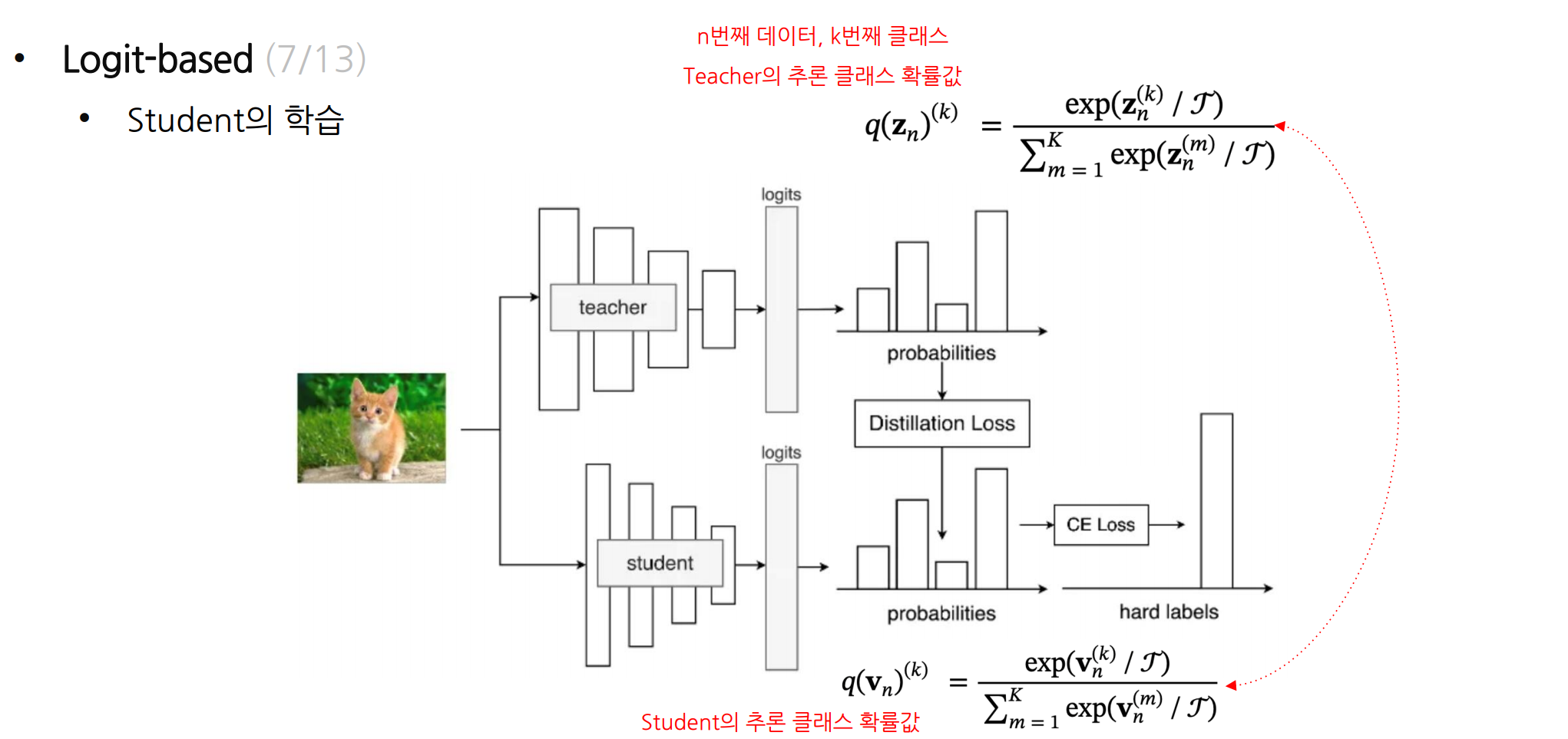
일반적인 분류기 학습 + 추가적으로, Teacher의 지식을 학습

Teacher의 지식 = 출력의 확률분포
따라서, Student는 자신의 클래스 예측이 선생의 클래스 예측이 유사해지도록 추가학습을 진행
👉 이 과정이 바로 지식 전달

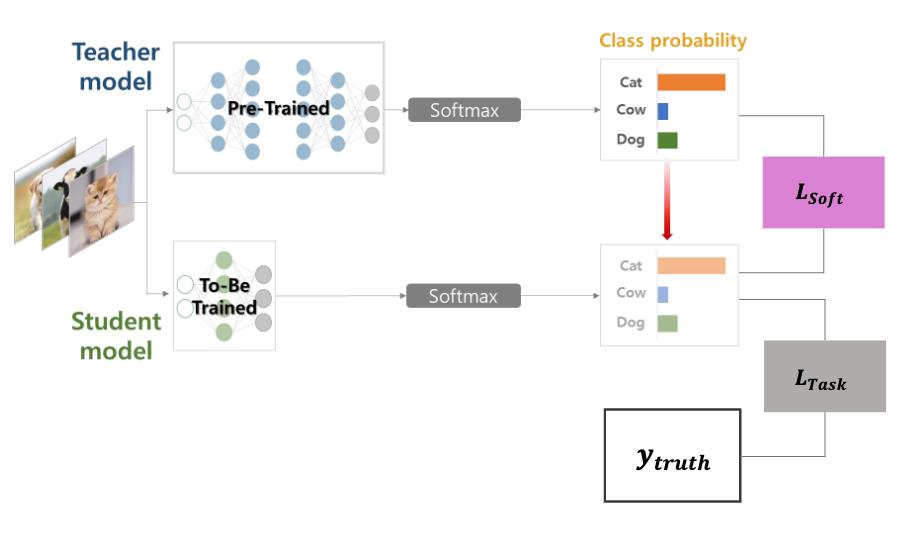
Teacher

분류 문제를 Cross-entropy Loss로 사전에 학습 (Hard Label)
이후 클래스 확률값(softmax 결과값)을 지식으로 전달

Student

분류 문제를 푸는 Cross-entropy Loss에 더해 (Hard Label)
Student의 확률값을 Teacher의 확률값으로 모사하는 KL-divergence Loss를 추가 (Soft Label)
확률값(분포)이 비슷한 정도: KL-divergence를 일반적으로 사용

Teacher의 학습

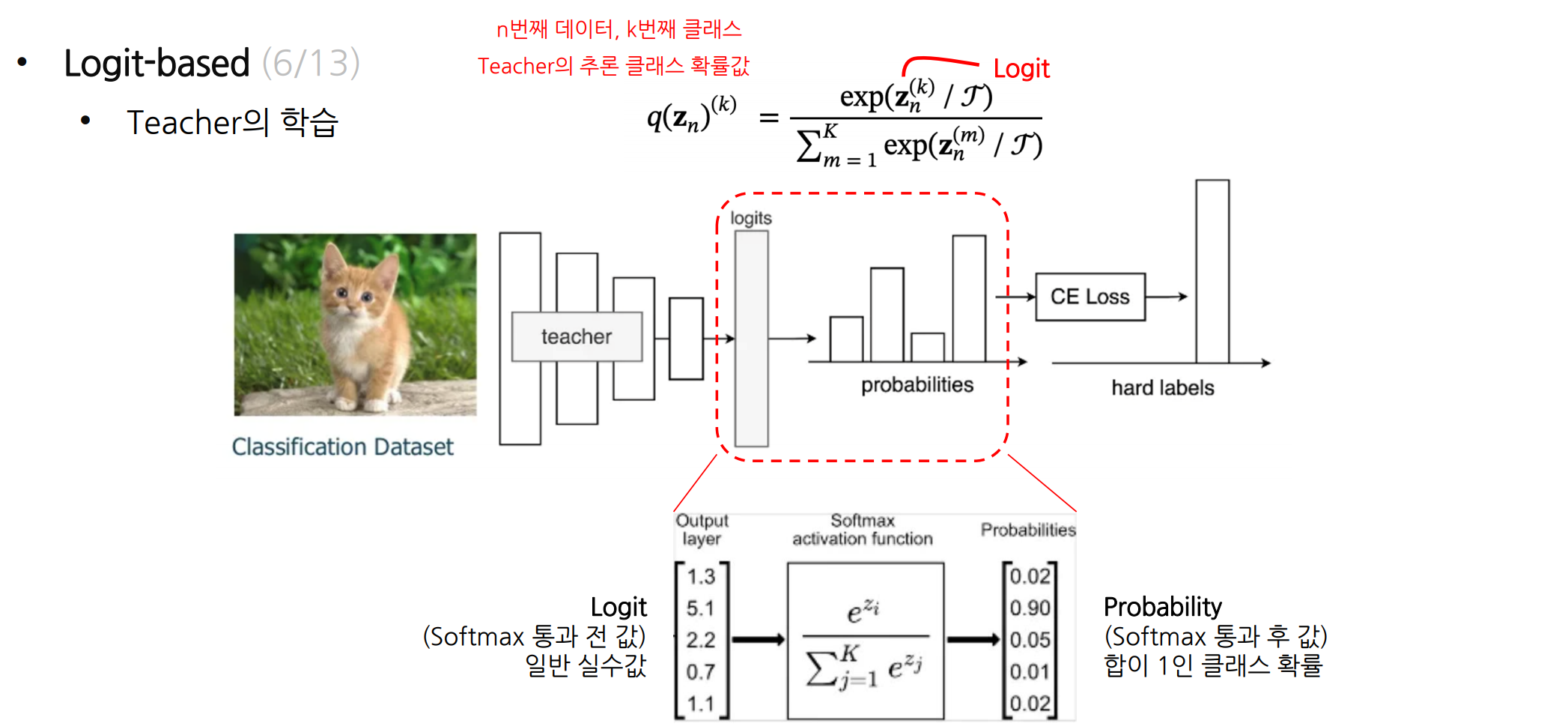
n번째 아이템, k번째 클래스

Teacher의 추론 클래스 확률값

q(z_n)^{(k)} = \frac{\exp\!\bigl(z_n^{(k)} / \mathcal{T}\bigr)}{\sum_{m=1}^{K} \exp\!\bigl(z_n^{(m)} / \mathcal{T}\bigr)}

Student의 추론 클래스 확률값

q(v_n)^{(k)} = \frac{\exp\!\bigl(v_n^{(k)} / \mathcal{T}\bigr)}{\sum_{m=1}^{K} \exp\!\bigl(v_n^{(m)} / \mathcal{T}\bigr)}

KL Loss (Soft Label)

\mathcal{L}_{\mathrm{KL}}\bigl(q(v_n) \mid q(z_n)\bigr) = \sum_{k=1}^K q(v_n)^{(k)} \,\log \!\biggl(\frac{q(v_n)^{(k)}}{q(z_n)^{(k)}}\biggr)

CE Loss (Hard Label)

\mathcal{L}_{\mathrm{CE}}\bigl(q(v_n),\,q(z_n)\bigr) = -\sum_{k=1}^K q(v_n)^{(k)} \,\log \! \bigl(q(z_n)^{(k)}\bigr)

Teacher의 loss: $\mathcal{L}_{\mathrm{CE}}$
Student의 loss: $\lambda_{\mathrm{CE}} \,\mathcal{L}_{\mathrm{CE}} \;+\; \lambda_{\mathrm{KL}} \,\mathcal{L}_{\mathrm{KL}}$
-> 여기서 헷깔리면 안되는것이 teacher의 $L_{CE}$ 랑 student의 $L_{CE}$ 가 다름
teacher는 정답과 비교한것이고
student도 정답과 비교한 것인데, teacher에 있는 L{CE}를 student의 L{CE}가 아니라는것..
즉, 결과적으로 수식 형태(CE)는 같아도, 실제로는 ‘Teacher 모델’과 ‘Student 모델’ 각각에 대해 따로 계산한다는 점에서 서로 다른 것

Temperature에 대해

q(z_n)^{(k)} = \frac{\exp\!\bigl(z_n^{(k)} / \mathcal{T}\bigr)}{\sum_{m=1}^{K} \exp\!\bigl(z_n^{(m)} / \mathcal{T}\bigr)}

모든 클래스에 대한 logit을 동일한 temperature로 나눈 후에 softmax를 적용
확률분포를 보다 날카롭게(T<1)/완만하게(T>1)변형

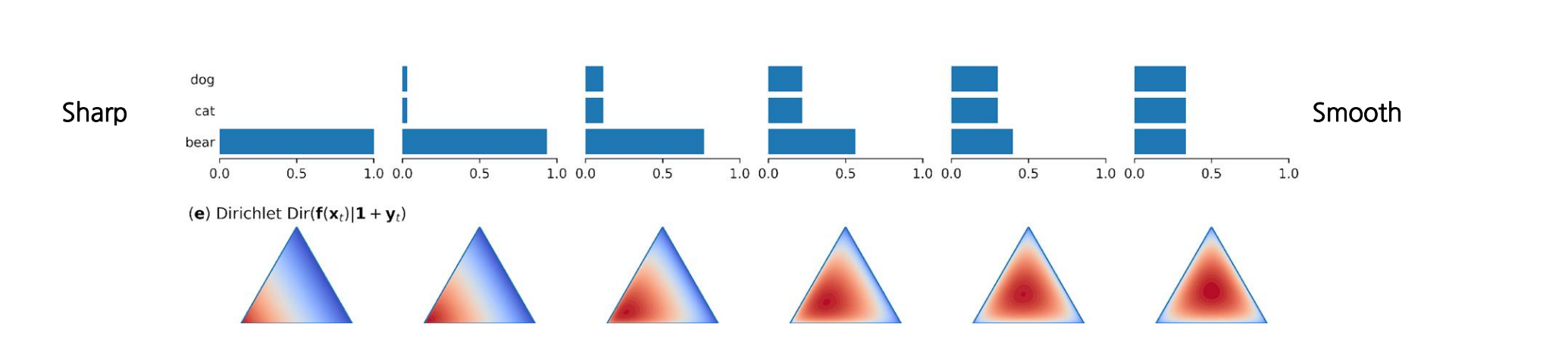
robustness가 증가해서 generalization 능력이 향상됨

2.2 PyTorch Tutorial

Teacher 모델

# Teacher 모델을 정의합시다. 평범한 CNN 기반 이미지 분류 모델입니다.
class Teacher(nn.Module):
	def __init__(self, num_classes=10):
	super(Teacher, self).__init__()
      self.features = nn.Sequential(
      nn.Conv2d(3, 128, kernel_size=3, padding=1),
      nn.ReLU(),
      nn.Conv2d(128, 64, kernel_size=3, padding=1),
      nn.ReLU(),
      nn.MaxPool2d(kernel_size=2, stride=2),
      nn.Conv2d(64, 64, kernel_size=3, padding=1),
      nn.ReLU(),
      nn.Conv2d(64, 32, kernel_size=3, padding=1),
      nn.ReLU(),
      nn.MaxPool2d(kernel_size=2, stride=2),
	)
  self.classifier = nn.Sequential(
    nn.Linear(2048, 512),
    nn.ReLU(),
    nn.Dropout(0.1),
    nn.Linear(512, num_classes)
    )
def forward(self, x):
  x = self.features(x)
  x = torch.flatten(x, 1)
  x = self.classifier(x)
  return x

student 모델

# Student 모델은 Teacher와 유사하지만 훨씬 shallow한 모델입니다.
class Student(nn.Module):
  def __init__(self, num_classes=10):
  	super(Student, self).__init__()
      self.features = nn.Sequential(
        nn.Conv2d(3, 16, kernel_size=3, padding=1),
        nn.ReLU(),
        nn.MaxPool2d(kernel_size=2, stride=2),
        nn.Conv2d(16, 16, kernel_size=3, padding=1),
        nn.ReLU(),
        nn.MaxPool2d(kernel_size=2, stride=2),
        )
      self.classifier = nn.Sequential(
        nn.Linear(1024, 256),
        nn.ReLU(),
        nn.Dropout(0.1),
        nn.Linear(256, num_classes)
        )
  def forward(self, x):
    x = self.features(x)
    x = torch.flatten(x, 1)
    x = self.classifier(x)
  return x