8. Video Generation
Video generation involves the model's creation of a new video, with or without
specific conditions.
Why Video Generation is necessary?
Creativity and Art,
Education and Training,
Media and Entertainment
8.1 Video Diffusion Models
처음으로 diffusion model를 활용해서 만든 영상

3D U-Net을 활용한 Video Diffusion 모델 구조
Video Diffusion 모델에서는 3차원(시간 + 2차원 공간) 정보를 동시에 다룰 수 있는 3D U-Net 구조를 사용합니다. 이 아키텍처는 일반적인 이미지용 2D U-Net과 달리, 시간 축을 추가하여 영상(frame) 단위의 특징을 추출하고, 이를 공간(Height × Width) 정보와 함께 종합적으로 처리합니다.
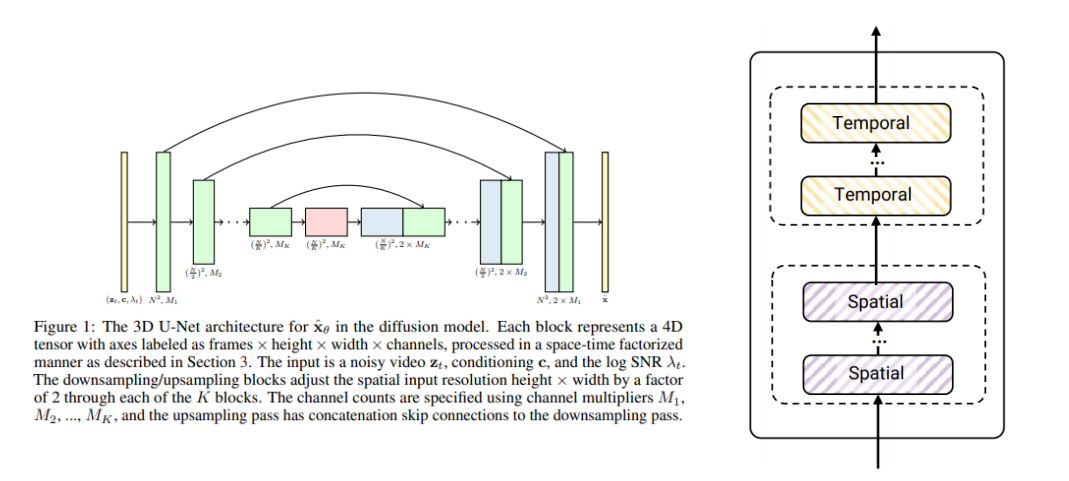
핵심 아이디어
-
입력 텐서 구조
- 4차원 텐서:
- : 프레임(시간) 수
- : 영상의 높이와 너비(공간 차원)
- : 채널 수
-
Diffusion 모델의 입력
- : 노이즈가 섞여 있는 영상(시점 에서의 noisy video)
- : 조건(conditioning) 정보 (예: 클래스, 텍스트 등)
- : log SNR(Signal-to-Noise Ratio)(신호 대 잡음비)
- 목표는 노이즈가 섞인 입력 를 깨끗한 영상 로 복원해 나가는 것
-
U-Net의 전체 구조
- 인코더(Downsampling) + 디코더(Upsampling) 구조
- 인코더: 영상의 공간 해상도를 단계적으로 절반씩 줄이면서 추상적인 특징을 추출
- 디코더: 낮아진 해상도를 다시 단계적으로 복원하며, 인코더에서 추출된 특징 지도(feature map)를 스킵 커넥션(skip connection)으로 전달받음
- 3D 블록으로 되어 있어, 시간 축(Temporal)과 공간 축(Spatial) 처리를 동시에 혹은 단계적으로 병렬/직렬 구성
- 각 Down/Up 블록마다 채널을 늘리거나 줄이는 채널 멀티플라이어 를 사용
공간-시간 분해(Spatial-Temporal Factorization)
3D U-Net은 공간 차원과 시간 차원을 별도로 혹은 병렬로 처리하기 위한 다양한 모듈을 포함할 수 있습니다:
-
Spatial 블록:
- 2D 커널(또는 3D 커널 중 공간 차원만 사용)을 사용해 영상의 차원을 주로 처리
- Down/Upsampling 시 해상도가 절반으로 축소/확장됨
-
Temporal 블록:
- 시간 축()에 대한 1D 커널(또는 3D 커널 중 시간 차원만 사용)로 순차적 혹은 병렬적으로 특징 추출
- 영상 시퀀스의 연속성/동작 정보를 포착하기 위함
아키텍처 구현 시, 공간-시간 합성곱 연산(3D Conv)을 바로 적용하거나, 구조를 좀 더 factorized 형태(예: (2+1)D Conv로 분리)로 적용하기도 합니다.
Downsampling & Upsampling
-
Downsampling (인코더 부분)
- 입력된 텐서를 공간 차원에서 2배씩 축소
- 예:
- 채널 수는 멀티플라이어 에 따라 늘어남
-
Upsampling (디코더 부분)
- Downsampling 단계에서 줄어든 해상도를 다시 키움
- 예:
- Skip Connection을 통해 인코더의 동일 단계 출력 특징과 결합(Concatenate)
채널 멀티플라이어(Channel Multipliers)
- :
- 각 Down/Up 블록마다 시작 채널 수의 배수를 결정
- 예: 초기 채널 수가 라면, 번째 블록에서의 채널 수는
- 일반적으로 는 낮은 해상도에서 더 많은 채널을 사용하여, 심도 있는 표현을 학습
모델 동작 과정
-
노이즈 섞인 영상 입력
- 시점 에서의 noisy video를 형태로 입력
- 조건 벡터 , log SNR 등 추가 정보도 함께 전달
-
인코더 (Downsampling) 단계
- 개의 Downsampling 블록으로 구성
- 각 블록에서 해상도를 절반으로 줄이고, 채널은 비율로 증가
- 3D 합성곱과 Activation(예: ReLU, SiLU 등), Normalization(예: GroupNorm 등)을 반복 적용
- 마지막 Downsampling 블록의 해상도는 매우 작아지지만, 채널은 크게 증가
-
중간 Bottleneck (Temporal + Spatial)
- 가장 낮은 해상도에서 시공간적 특징을 심층적으로 변환
- 여러 Residual 블록 또는 Attention 메커니즘 등을 포함해, 전역 정보를 학습
-
디코더 (Upsampling) 단계
- Downsampling의 역순으로 진행
- 해상도를 2배씩 복원하면서, 해당 단계 인코더 특징을 Skip Connection을 통해 Concatenate
- 채널 수는 Downsampling과 반대로 줄어듦(멀티플라이어 역순 적용)
-
출력
- 최종적으로 깨끗한 영상에 대한 예측값(또는 노이즈 예측)을 출력
- Diffusion 모델에서는 를 통해 역확산 과정을 거쳐 실제 영상 복원을 수행
예시 (간단한 의사 코드)
아래는 3D U-Net의 Down/Up 블록 구조를 간단히 나타낸 의사 코드입니다.
class Conv3DBlock(nn.Module):
def __init__(self, in_ch, out_ch, kernel_size=3, stride=1, padding=1):
super().__init__()
self.conv = nn.Conv3d(in_ch, out_ch, kernel_size, stride, padding)
self.norm = nn.GroupNorm(num_groups=8, num_channels=out_ch)
self.act = nn.SiLU() # 또는 ReLU, LeakyReLU 등
def forward(self, x):
return self.act(self.norm(self.conv(x)))
class DownBlock(nn.Module):
def __init__(self, in_ch, out_ch):
super().__init__()
self.conv1 = Conv3DBlock(in_ch, out_ch)
self.conv2 = Conv3DBlock(out_ch, out_ch)
self.pool = nn.MaxPool3d(kernel_size=2)
def forward(self, x):
x = self.conv1(x)
x = self.conv2(x)
x_down = self.pool(x)
return x_down, x # Skip 용도
class UpBlock(nn.Module):
def __init__(self, in_ch, out_ch):
super().__init__()
self.up = nn.Upsample(scale_factor=2, mode='trilinear', align_corners=False)
self.conv1 = Conv3DBlock(in_ch, out_ch)
self.conv2 = Conv3DBlock(out_ch, out_ch)
def forward(self, x, skip):
x = self.up(x)
# Skip connection (concat)
x = torch.cat([x, skip], dim=1)
x = self.conv1(x)
x = self.conv2(x)
return x8.2 Video Probabilistic Diffusion Models in Projected Latent Space(PVDM)
이 모델은 동영상 데이터를 직접 3차원(시간 + 공간) 구조로 처리하기보다는,
3D→2D 형태로 투영한 잠재 공간(latent space)에서 Diffusion 모델을 수행함으로써
효율적인 학습과 생성 품질 향상을 목표로 합니다.
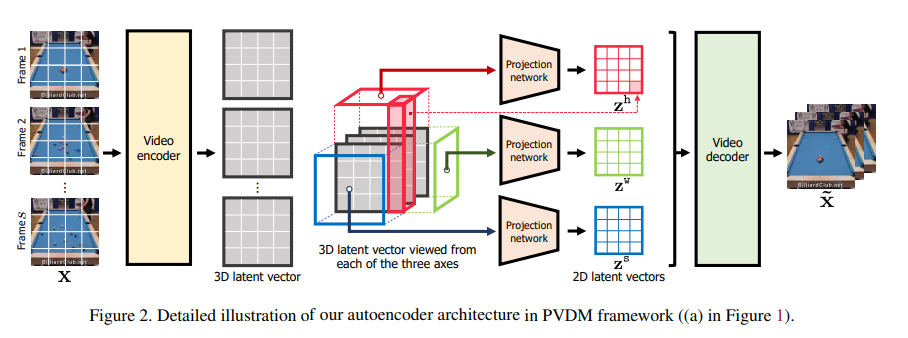
개념 요약
-
오토인코더 (Autoencoder) 구조
- 비디오 인코더를 통해, 원본 비디오 를 3D 잠재 벡터로 변환
- 이 3D 잠재 벡터는 차원을 유지한 채로, 채널 수만 축소된 형태
- 이후 프로젝션 네트워크 (Projection network)를 이용해,
- 시간축,
- 높이축,
- 너비축
각각을 기준으로 2D 형태로 투영한 뒤, 3개의 2D 잠재 벡터 를 얻음
- 비디오 디코더는 다시 이들 2D 잠재 벡터들을 3D 형태로 통합(역투영)하고,
최종적으로 복원된 비디오 를 출력
-
Diffusion 모델
- 오토인코더가 생성한 2D 잠재 벡터들에서, 실제 2D 이미지처럼 Diffusion 과정을 수행
- 시간 단계별로 노이즈를 추가하고 제거(denoising)하는 과정을 통해,
- 노이즈 섞인 잠재 공간에서
- 점진적으로 깨끗한 잠재 표현으로 복원
- 이때 Diffusion 모델 아키텍처는,
- Downsample / Upsample 레지듀얼 블록,
- Attention 레이어,
- 기타 U-Net형 구조
등을 활용해, 2D 이미지-like 구조에서 효과적으로 노이즈를 제거함
-
Projected Latent Space
- 3D 비디오 픽셀()을
3개의 2D 투영(예: , , )으로 압축, 인코딩 - 이 2D 변환으로 인해,
- 3D 합성곱을 다루는 복잡도가 줄어듦 (모델 파라미터 감소, 연산량 감소)
- 기존의 2D Diffusion 모델 기법(예: 이미지용 Diffusion)을 재활용 가능
- 각각의 2D 투영을 독립적으로 Diffusion 처리하거나 합쳐서 한 번에 처리할 수도 있는 유연한 설계
- 3D 비디오 픽셀()을
상세 흐름
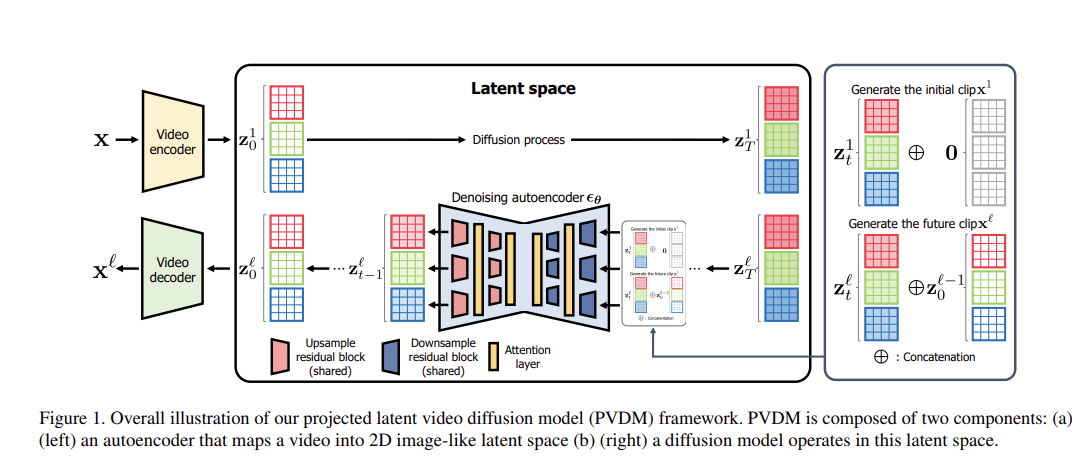
1. 원본 비디오 입력
- (예시)
- : 프레임 수 (Time), : 공간 해상도, 채널 수(3)는 RGB
-
비디오 인코더
- 3D Convolution, 2+1D Convolution, 혹은 변형된 CNN/RNN 등으로 구성 가능
- 입력 비디오의 시공간 정보를 압축하여,
3D 잠재 벡터 를 생성- 여기서 , , 는 축소된 시공간 해상도
- 는 잠재 표현에서의 채널 수
-
프로젝션 네트워크
- 3D 잠재 벡터 를 세 축 방향으로 각각 2D 투영
- 예시:
- Height 축:
- Width 축:
- Spatial(또는 Temporal) 축:
- 이 과정을 통해, 3D 텐서를 3개의 2D 텐서로 분리해서 얻음
-
Diffusion 모델
- 각각의 2D 잠재 맵 에 대해 노이즈 추가→노이즈 제거 과정을 수행
- 2D U-Net 혹은 변형된 Diffusion 아키텍처로 단계별로 잠재 벡터를 정제(denoise)
- 결과적으로 노이즈가 제거된 2D 잠재 벡터를 얻음
- Diffusion 과정은 여러 타임스텝 을 거치며 각 시점에서 노이즈 비율(예: )을 조절
-
비디오 디코더 (역투영 + 복원)
- Diffusion을 거쳐 깨끗해진 2D 잠재 벡터
→ 다시 3D 형태로 결합 (역투영, 또는 3D 재구성) - 최종적으로,
- 비디오 디코더가 이를 입력받아,
- 원본 해상도로 비디오 를 재구성
- Diffusion을 거쳐 깨끗해진 2D 잠재 벡터
요약
Projected Latent Video Diffusion Model (PVDM)은 비디오를 3차원 전체로 한 번에 다루는 대신, 3D 잠재 벡터를 2D 투영으로 변환하여 Diffusion을 수행함으로써,
- 연산량 절감,
- 2D Diffusion 노하우 활용,
- 시공간 일관성 유지
등의 이점을 얻는 모델입니다.
8.3 Align your Latents: High-Resolution Video Synthesis with Latent Diffusion Models
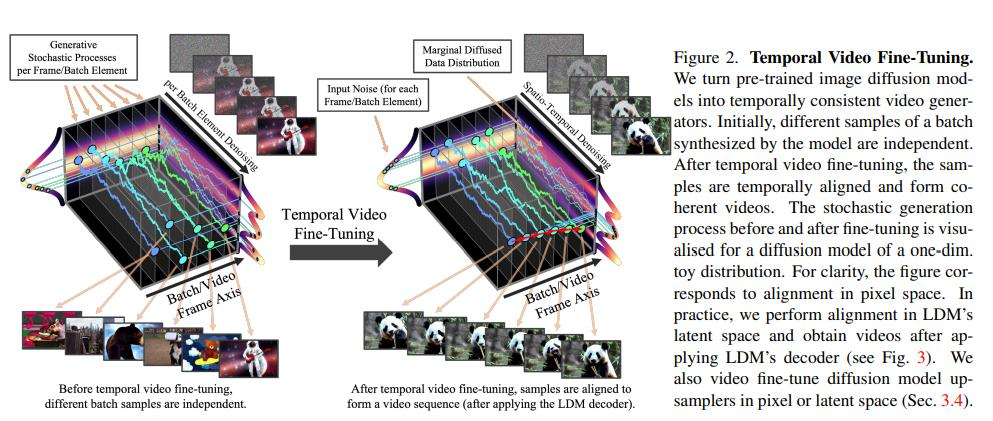
Temporal Video Fine-Tuning
이 그림은 기존에 학습된 이미지 확산(Diffusion) 모델을 이용해 시간적으로 일관성 있는 동영상을 생성하는 과정을 보여줍니다.
- 좌측(Before temporal video fine-tuning):
- 사전에 학습된 이미지 확산 모델이 프레임 단위로 독립적인 샘플(이미지)을 생성
- 배치(batch) 내의 서로 다른 샘플(프레임)들이 시간적 연관성이 없이 독립적으로 생성되어, 영속적인 비디오 시퀀스를 이루지 못함
- 우측(After temporal video fine-tuning):
- Temporal Video Fine-Tuning 과정을 거쳐,
- 이전엔 독립적이던 배치 샘플들이 시간적으로 정렬(Aligned)되어,
- 연속적인 동영상 형태로 변환
- 즉, 배치의 각 요소가 연속 프레임처럼 연결되어 자연스러운 시퀀스를 형성
과정 요약
-
사전 학습된 이미지 Diffusion 모델 준비
- 일반 이미지 생성에 최적화된 이미지 모델
- 프레임 단위 샘플(정적 이미지)을 생성하는 데 특화
-
동영상 데이터에 대한 Fine-Tuning
- 사전 학습 모델을 “Temporal Video Fine-Tuning” 기법으로 재학습
- Fine-Tuning 시,
- 인접 프레임 간 일관성(Temporal Consistency)을 학습하도록
- 공동 분포를 맞추는 방향으로 모델을 조정
-
결과
- 독립적이었던 이미지 생성이 연속된 비디오 프레임 생성으로 전환
- 시간적 연결성(Temporal Alignment)을 확보해,
- 동일한 대상이나 배경이 프레임마다 유지되는 등
- 부드러운 동영상을 얻을 수 있음
그림 해석
-
좌측:
- “Generative Stochastic Processes per Frame/Batch Element”로 표시된 부분은
각 프레임이 독립적으로 생성된다는 것을 의미 - 여러 샘플이 있더라도, 각각은 별개의 이미지로 취급되어,
비디오처럼 이어지지 않음
- “Generative Stochastic Processes per Frame/Batch Element”로 표시된 부분은
-
중간:
- “Input Noise(for each Frame/Batch Element)”는 Diffusion 모델이 이미지별로 노이즈를 추가-제거하는 과정을 반복해 각 이미지(프레임)를 생성함
- 하지만 여전히 프레임 간 공유 정보나 시간적 상관 고려가 부족
-
우측:
- “Temporal Video Fine-Tuning”을 수행한 후,
- 생성된 프레임들이 시퀀스 형태로 맞춰짐 (Align)
- 스토캐스틱(확률적) 생성 과정이 프레임 간 시간적 연관성을 반영하여 일관성 있는 동영상 시퀀스를 만듦
- 실제로는 Latent Diffusion Model(LDM)의 잠재 공간에서 정렬을 수행하고 최종 디코더를 거쳐 픽셀 공간의 영상을 복원
- Fine-Tuning된 Diffusion 모델로,
- 동영상에서 부드러운 전이,
- 연속적 모션,
- 장면 일관성을 유지하며 생성 가능
- “Temporal Video Fine-Tuning”을 수행한 후,
Temporal Video Fine-Tuning with Fixed Image Backbone
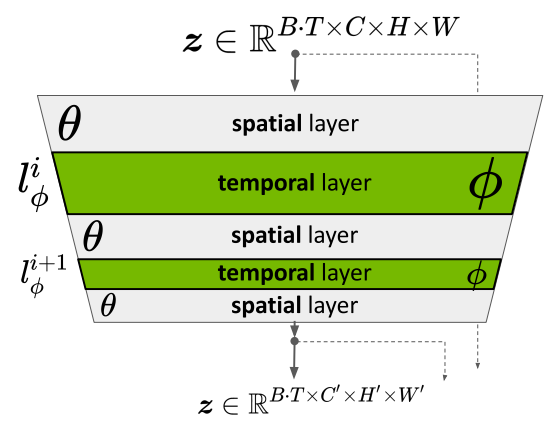
위 그림은 이미지 기반 확산 모델(LDM, Latent Diffusion Model)을 동영상으로 확장하기 위해,
- 공간(spatial) 처리를 담당하는 이미지 백본(Backbone) 와
- 시간(temporal) 처리를 담당하는 추가 레이어 로 나누어 설계된 구조를 보여줍니다.
주요 아이디어
-
이미지 백본() 고정
- 는 사전에 학습된 LDM(이미지용 Diffusion 모델)의 파라미터
- 공간 해상도를 처리하는 역할
- Fine-Tuning(미세 조정) 단계에서는 갱신되지 않음 (고정된 상태로 유지)
- 이미 뛰어난 이미지 생성 능력을 갖춘 모델을 활용해, 시간 차원의 학습 비용을 줄임
-
시간 레이어()만 학습
- 그림 속 녹색(temporal layer) 부분이
- 배치 시간 채널 높이 너비 형태의 입력()에 대해,
시간 축(temporal dimension) 처리를 전담 - Fine-Tuning 동안 만 학습(업데이트)
- 이를 통해 프레임 간 일관성(Temporal Consistency)을 확보
-
구조
- Spatial Layer:
- 로 표시된 층
- 기존의 이미지 기반 합성곱(혹은 UNet 블록 등)이 이 역할을 수행
- 이미지 처리, 해상도 축소/확대, 채널 변환 등 수행
- Temporal Layer:
- 로 표시된 층
- RNN, 1D Conv(시간축), Attention, 혹은 맞춤형 레이어 등을 사용
- 각 프레임 간 상호 작용을 학습해, 연속된 동영상으로 변환
- Spatial Layer:
학습 과정 개요
-
사전 학습된 LDM() 준비
- 고품질 이미지 생성을 가능케 하는 이미지 Diffusion 모델
- 공간 정보 처리에 특화
-
동영상 Fine-Tuning
- 별도의 Temporal Layer()를 추가/삽입해 프레임들 사이의 시간적 연관성을 학습
- 이때 (이미지 백본)는 고정하고,
- (시간 레이어)만 업데이트
- 결과적으로 프레임마다 일관된 객체와 배경 정보, 모션을 유지하는 동영상을 생성
-
추론(Inference)
- 학습 후, 입력 노이즈(또는 조건)를 넣으면
- Spatial Layer()가 이미지를 잘 처리하고,
- Temporal Layer()가 프레임 간 자연스러운 연결성을 확보
- 최종적으로 시간적으로 일관성 있는 비디오를 출력
결론
이 구조에서는
- 이미 학습된 이미지 백본()을 활용해 공간 정보를 처리하고
- 추가된 시간 레이어()를 통해 프레임 간 연속성을 학습함으로써
시간적으로 일관성 있는 비디오를 생성할 수 있습니다.
Fine-Tuning 시에는 는 고정하고, 만 업데이트하므로,
- 파라미터 효율적
- 이미지 모델의 이미 확보된 성능을 그대로 활용하며 동영상 생성 능력을 빠르게 습득하게 됩니다.
9. 2d to 3d
The goal of the 2d to 3d is to produce high quality 3d object from 2d image or 2d prior models
2D모델을 3D로 바꾸는 것은 다른 차원의 이야기인데!!
Why 2d to 3d is necessary?
3D 모델 학습에는 대규모 3D 데이터가 필요하지만, 실제로 3D 데이터는 부족하고 제작도 어렵습니다.
대신, 대규모 2D 데이터의 풍부한 정보를 활용하면 적은 3D 데이터로도 고품질 3D 생성을 수행할 수 있습니다.
이 방식은 한정된 3D 데이터 자원을 보완하고 대량의 3D 데이터를 확보하기 어려운 문제를 해결합니다.
9.1 DreamFusion: Text-to-3D using 2D Diffusion
배경 (Background)
- NeRF (Neural Radiance Fields)
- 3D 공간 상의 물체·장면을 2D 영상들을 통해 표현하는 모델
- 서로 다른 카메라 각도·시점에서 촬영된 다수의 이미지를 입력으로 받아,
밀도(density) 및 색깔(color)에 대한 방사율(radiance) 함수를 학습 - 학습이 끝나면, 아무 각도에서든 해당 장면을 렌더링(rendering) 가능
Diffusion Models and Score Distillation Sampling
DreamFusion은 텍스트에서 3D 장면을 생성하기 위해, 2D Diffusion 모델(예: Imagen)을 활용합니다.
이 과정에서 Score Distillation Sampling (SDS) 기법을 사용하여,
NeRF와 같은 3D 표현(예: )의 파라미터를 효율적으로 업데이트합니다.

1. 기본 수식:
우선 2D Diffusion 모델에서 사용하는 일반적인 손실(단계 에서 노이즈 제거를 학습하는 목적)
는 다음처럼 표현할 수 있습니다.
- : Diffusion 모델(예: U-Net)에서 예측한 노이즈
- : 실제 데이터(또는 생성하고자 하는 이미지)
- : Diffusion 타임스텝(0에서 1 사이)
- : 일정(schedule)에 따른 스케일 파라미터
- : 가중치 함수 (타임스텝마다 달라질 수 있음)
- : 시점 에서 노이즈가 섞인 상태의 샘플
- : 텍스트 등 조건(conditional) 정보
1.1 파라미터 업데이트 식
이때, 라고 두면(예: 3D 표현에서 렌더링한 이미지를 로 봄),
Diffusion 모델의 노이즈 예측 결과를 기준으로 에 대해 역전파가 일어납니다.
Noise Residual:
U-Net Jacobian:
Generator Jacobian: , 여기서
- 우측에서 U-Net(또는 Diffusion 모델) 쪽의 Jacobian( )을 생략(omit)하여 파라미터 쪽으로만 미분이 이어지도록 하는 것이 Score Distillation Sampling (SDS)의 핵심 아이디어 중 하나입니다.
2. Score Distillation Sampling (SDS)
DreamFusion에서는 라는 손실을 정의해 NeRF(또는 3D MLP)의 파라미터 가 2D Diffusion 모델이 예측한 노이즈와 실제 노이즈의 차이를 줄이도록 학습시킵니다.
2.1 정의
- 이는 의 업데이트 식에서 U-Net( )의 Jacobian 항을 생략한 형태로 볼 수 있습니다.
- 결과적으로, 2D Diffusion 모델에서 얻은 노이즈 예측 오차만으로 3D 파라미터()가 직접 업데이트됩니다.
- 논문/코드에 따라 추가적으로 KL 항이나 등 정규화 항이 포함되기도 합니다.
예시 형태:
3. DIP(Differentiable Image Parameterization)와 연결
- DreamFusion에서 는 NeRF처럼 3D를 파라미터화한 MLP를 통해 랜덤 시점에서 렌더링한 2D 이미지입니다.
- SDS는 렌더링된 이미지가 텍스트 조건에 부합하도록 Diffusion 모델(예: Imagen)의 노이즈 예측을 이용해 MLP()를 업데이트합니다.
- 즉, 픽셀 단위가 아니라, 랜덤 각도로 렌더링된 영상 단위로 학습이 진행되어, 3D 구조(NeRF)가 텍스트에 맞게 최적화됩니다.
4. Ancestral Sampling vs. Score Distillation Sampling
-
Ancestral Sampling:
- 일반적인 Diffusion 과정에서, 픽셀(또는 잠재 공간) 단계에서 점진적으로 샘플을 업데이트
- 최종적으로 이미지를 샘플링
-
Score Distillation Sampling (SDS):
- NeRF(또는 3D) 파라미터 공간 에서 SGD/역전파를 통해 업데이트
- Diffusion 모델 자체의 파라미터는 고정 (이미 학습된 상태)
- U-Net Jacobian을 무시함으로써,
- NeRF 파라미터가 Diffusion 모델의 노이즈 예측 스코어만 보고 직접 학습
요약
- : 2D Diffusion 손실 정의
- : 그 손실에서 U-Net Jacobian을 제외하여 NeRF 같은 3D 모델 파라미터에만 직접 역전파
- DreamFusion:
- 텍스트 조건을 갖춘 2D Diffusion(Imagen)을 활용
- 랜덤 카메라로 3D 모델을 렌더링 → 2D Diffusion 노이즈 예측으로 손실 계산 → 3D 파라미터 업데이트
- 결과적으로 고품질 3D 장면을 텍스트에서 생성 가능
이로써 DreamFusion은 픽셀 대신 랜덤 시점을 통해 3D 모델(NeRF)을 최적화하는 Score Distillation Sampling 방식을 구현합니다.
DreamFusion Algorithm
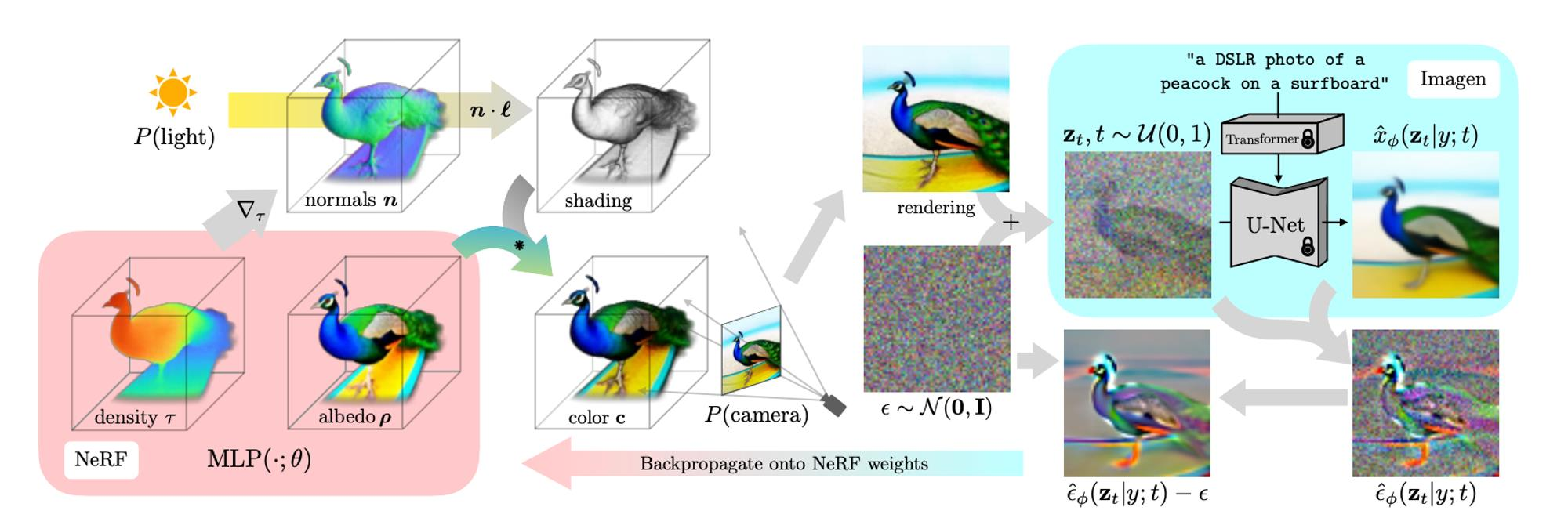
-
NeRF 측(왼쪽)
- Density(), Albedo(), Normals() 등을 출력하는 MLP
- 이를 기반으로 조명(빛, ), 카메라()를 적용해 2D 렌더링 결과(이미지) 생성
-
Diffusion 측(오른쪽)
- Imagen(Text-to-Image Diffusion) 모델이 노이즈가 섞인 상태의 이미지 를 텍스트(“a DSLR photo of a peacock on a surfboard”) 조건으로 노이즈 제거(denoise)
- 노이즈 예측치 를 토대로 SDS Loss()를 계산
- 이 손실을 NeRF 파라미터에 역전파(Backpropagate)하여 NeRF가 텍스트 조건에 맞게 렌더링을 수정하도록 학습
-
최종 결과
- NeRF는 텍스트에 부합하는 3D 장면(예: 공작이 서핑보드 위에 있는 모습)을 표현
- 학습 완료 후, 아무 시점에서나 고해상도 3D 렌더링을 얻을 수 있음
요약
- NeRF: 3D를 표현하는 강력한 방법, 하지만 텍스트 제어가 직접적으로 어려움
- DreamFusion:
- 기존 Text-to-Image Diffusion(Imagen)의 생성 능력과
- NeRF의 3D 표현력을 결합
- SDS Loss를 통해, 2D 확산 모델의 노이즈 예측 정보를 네트워크(NeRF)에 역전파하여 3D를 학습
- 결과적으로, 텍스트만으로도 3D 모델(NeRF)을 생성·제어 가능
- 수많은 시점에서 일관성 있는 영상 (view synthesis) 확보
- 3D 데이터 없이도(또는 아주 적게 사용하면서) 고품질의 3D를 만들 수 있음
9.2 zero-1-to-3: zero-shot one image to 3d object
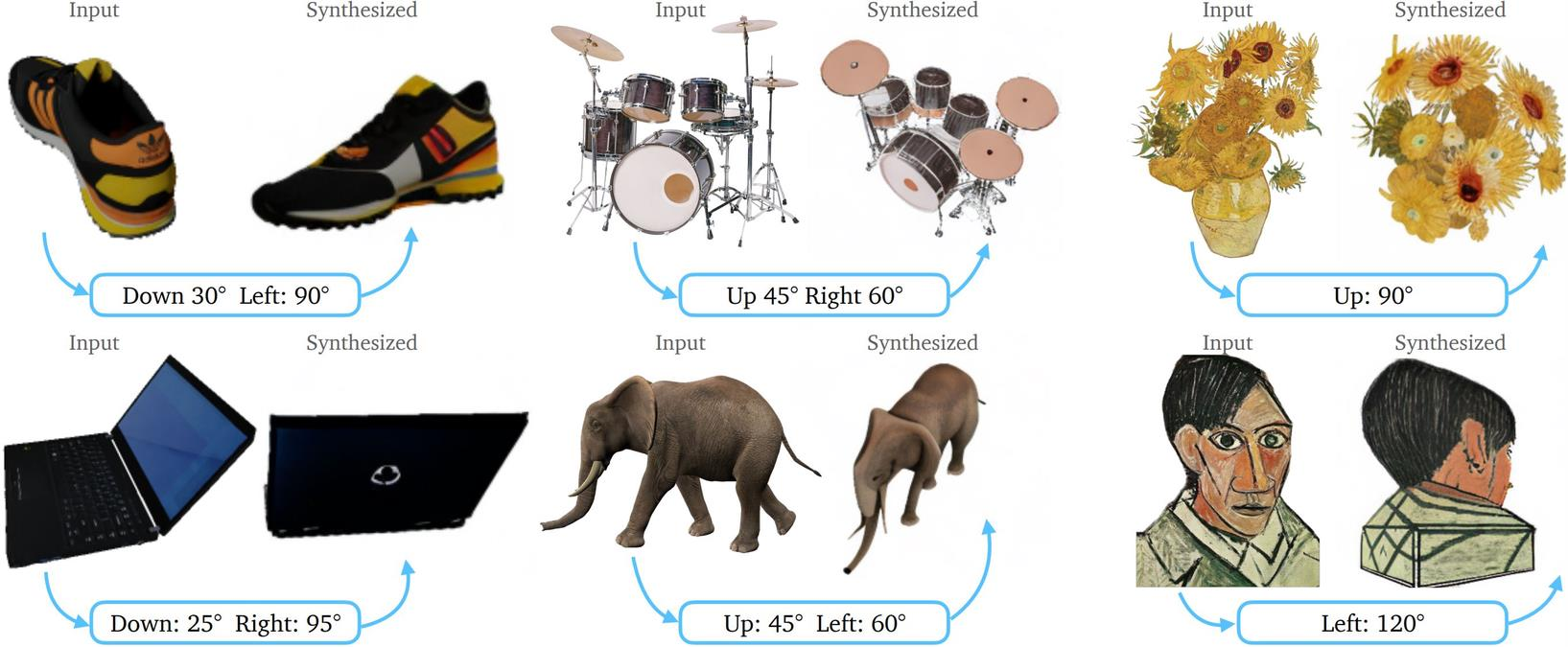
DreamFusion의 해상도 및 속도 이슈
- DreamFusion은 텍스트→3D 생성에서 고해상도(예: 256×256 이상)로 직접 최적화를 진행하면 연산량이 매우 많아 속도가 극도로 느려지는 문제가 있습니다.
- 이를 해결하기 위해 64 해상도 수준으로 실험을 진행하며 이때도 약 1.5시간 정도의 학습 시간이 소요됩니다.
- 이는 실제 응용 환경에서 더 빠른 3D 생성이 필요함을 보여주므로,
학습 가속화를 위한 연구가 중요합니다.
- 이는 실제 응용 환경에서 더 빠른 3D 생성이 필요함을 보여주므로,
배경
- Stable Diffusion 등의 대규모 확산 모델을 미세조정(Fine-tuning)하여 카메라 시점(Camera Viewpoint)을 제어하는 기법을 연구
- 이를 통해, 이미지를 학습된 모델로 인코딩한 뒤,
임의의 카메라 시점(원하는 각도)에서 디코딩 → 새로운 뷰를 생성 - 나아가, 제로샷(Zero-Shot)으로도 다양한 실제 이미지(“in-the-wild”)에 적용 가능
View-conditioned Diffusion
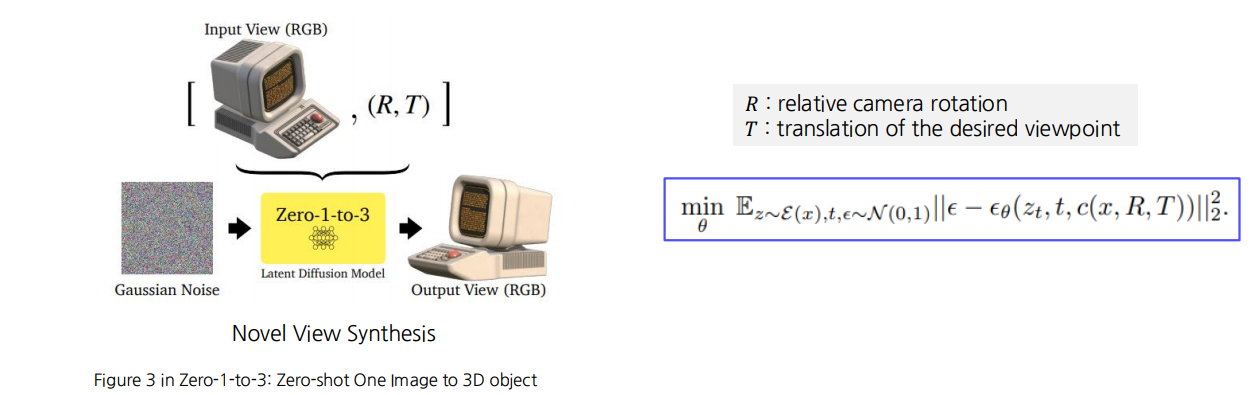
개요
- Stable Diffusion만으로는 카메라 시점(Viewpoint)을 다양하게 제어하기 어려움
- 따라서 사전 학습된 Diffusion 모델을 이미지 쌍과 카메라 외부 파라미터(extrinsic) 정보인 를 이용해 미세 조정(Finetuning)
- 이를 통해 모델이 카메라 회전(Rotation), 이동(Translation)과 같은 시점 변환 기법을 학습하게 됨
카메라 외부 파라미터
- : 상대 카메라 회전(Relative camera rotation)
- : 카메라 이동(Translation), 즉 원하는 시점/좌표로의 이동량
수식
미세 조정된 모델(예: )은
입력 이미지 와 시점 변환 정보 를 조건()으로 사용합니다.
Diffusion 과정에서,
- 노이즈 ,
- 시간 스텝 ,
- 랜덤 변수 (해당 시점에서 노이즈가 섞인 상태),
을 통해 다음과 같은 목표 함수를 최소화합니다.
- : 입력 이미지 $ x $에서 유도되는(또는 렌더링·주사) 잠재 샘플
- : 미세 조정된 Diffusion U-Net이 노이즈를 예측하는 함수
- :
- 조건(Condition)으로써,
- 원본 이미지 와 카메라 변환 정보 를 결합한 것
- 모델이 “원본 이미지를 로 변환한 시점의 뷰”를 생성하도록 유도
작동 방식 (개념 흐름)
-
입력 뷰 (RGB)
- 원본 이미지 (예: 어떤 사물의 단일 시점 사진)
-
카메라 변환 정보
- 원하는 새 시점(회전 + 이동)에 해당
- 예: “이 사물을 45도 회전, 오른쪽으로 약간 이동한 시점으로 보고 싶다”
-
Zero-1-to-3 Latent Diffusion Model
- 초기 노이즈 에서 시작
- 점진적으로 노이즈를 제거하면서 출력 뷰를 생성
- 이때 조건으로 를 사용하여,
원본 이미지가 시점으로 변환된 결과를 출력
-
Output View (RGB)
- 새 시점에서 각도가 달라진 2D 이미지(또는 나아가 3D 형태)
- Novel View Synthesis: 단일 시점 이미지만 갖고도,
미세 조정된 모델이 새로운 시점을 합성
3D Reconstruction in Zero-1-to-3

이 그림은 단일 이미지(예: 체어 사진)로부터, 상대 카메라 회전()과 이동()을 통해
새로운 시점에서 볼 수 있는 3D 재구성을 수행하는 과정을 보여줍니다.
개요
- 입력 View + (R, T)
- 원본 이미지를 입력으로 받고,
- 원하는 시점(회전 , 이동 ) 정보를 같이 전달
- Zero-1-to-3 모델
- 뷰 변환(상대 시점 변환)을 고려하여,
- Volumetric Rendering을 수행하거나 Neural Field(3D 표현)를 업데이트
- 렌더링된 결과
- 입력 뷰와 비교하여 Loss를 계산 (예: 등)
- Neural Field(또는 3D 표현)의 파라미터를 점진적으로 개선
- 최종 3D 재구성
- 다양한 카메라 각도에서 렌더링 가능한 3D 객체를 얻음
등장하는 Loss:
1. 기호 설명
- :
- 여기서 “SJC”는 Score-based Joint Consistency 등으로 불릴 수 있음(논문 용어에 따라 다름).
- 새로운 시점으로 렌더링한 결과 에 대해 확률 분포(또는 Score) 관점에서 일관성을 맞추는 손실을 나타냄.
- :
- 시점(카메라 파라미터) 에서 렌더링된 이미지(또는 해당 표현)
- :
- 가 노이즈 수준 에서 따르는 분포를 의미하거나,
- Score 기반의 확률 모델(논문에 따라 미세하게 정의가 다를 수 있음)
- :
- 이미지(또는 렌더링 결과) 에 대한 편미분(Gradient)
- 이를 통해 Neural Field 혹은 Volumetric Rendering 파라미터에 역전파할 수 있게 됨
2. 해석
- 형태이므로 확률 분포의 로그 우도(Log-likelihood)에 대한 Gradient
- 3D 형태(Neural Field)에서 시점 로 렌더링된 2D 이미지 가 특정 분포/score에 부합하도록 업데이트함
- 결과적으로 3D 표현이 “정해진 뷰”에서 타당한 이미지를 생성하도록 파라미터가 학습됨
요약
Zero-1-to-3는 단일 입력 이미지만으로도 원하는 카메라 시점(회전 , 이동 )에서의 새로운 뷰를 생성하는 기법입니다. 이를 위해 Stable Diffusion 기반 모델에 카메라 외부 파라미터를 조건으로 주어 미세 조정을 수행합니다. 그 결과, 모델은 노이즈 예측 에러 를 최소화하며, 카메라 변환을 반영해 일관성 있는 새 시점 이미지를 생성할 수 있게 됩니다.
구체적으로는,
- Volumetric Rendering을 통해 Neural Field(3D MLP)가 예측한 밀도/색 정보를 (R, T) 시점으로 2D 이미지로 렌더링하고,
- 이에 대해 , 등 다양한 손실을 계산하여 모델을 업데이트합니다.
- 이렇게 다양한 시점으로 반복 학습함으로써, 최종적으로 3D 객체가 실제 시점 변환과 일관성을 지니도록 학습됩니다.
즉, Zero-1-to-3는 하나의 입력 이미지()와 원하는 시점 정보()만 주어져도 Zero-shot Novel View를 만들 수 있으며 Neural Field(볼류메트릭 표현)가 시점 변환된 이미지를 합리적으로 생성하도록 Score 기반 손실( 등)을 통해 핵심 파라미터를 업데이트한다는 점이 특징입니다.
9.3 Consistent-1-to-3: Consistent Image to 3D View Synthesis via Geometry-aware Diffusion Models
이 방법은 소수(혹은 단일)의 2D 이미지 뷰로부터 일관성 있는 3D 뷰를 생성하기 위해,
- SRT(Set-Latent Representation + Ray-based Rendering)
- View-conditioned Diffusion
두 가지 아이디어를 결합한 프레임워크입니다.
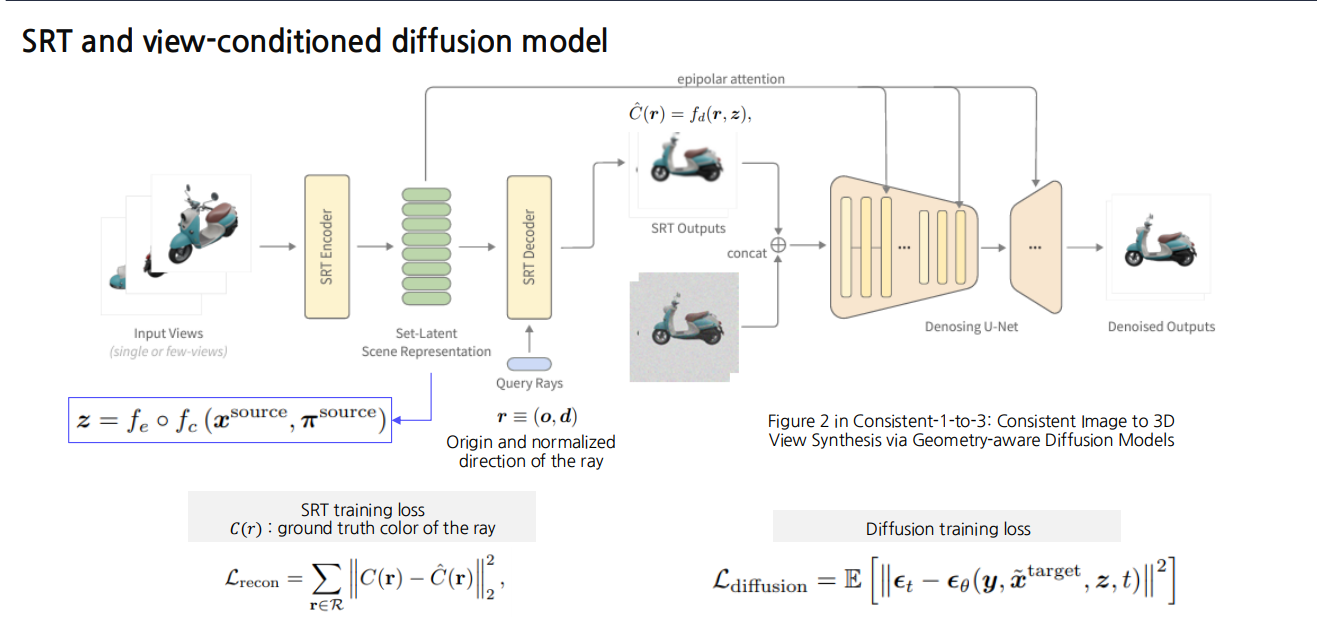
전체 파이프라인 요약
-
입력 뷰:
- 하나 혹은 소수의 이미지를 입력으로 받음 (예: 스쿠터 이미지를 다양한 각도에서 몇 장만 찍은 경우)
-
SRT Encoder:
- 입력 이미지 와 해당 카메라 매개변수(포즈) 를 카메라 인코딩 함수 로 먼저 처리한 뒤,
- 장면 임베딩(세트-잠재 표현, )을 생성
-
SRT Decoder:
- 새로운 시점 쿼리(광선) 를 입력받아,
- (장면 임베딩)와 결합해 픽셀 색 를 예측
-
Denoising U-Net (Diffusion 모델):
- SRT Decoder 출력(또는 중간 결과)와 결합해 노이즈 제거(U-Net) 과정을 수행
- 최종적으로 노이즈가 제거된(Denoised) 이미지를 출력
주요 구성 요소 및 Loss
1. SRT Training Loss ()
SRT 자체를 학습할 때는, 주어진 레이(rays) 집합 에 대해 예측 색 와 실제 색 의 차이를 최소화합니다.
- : 실제(또는 Ground Truth)로 관측된 광선 의 컬러
- : SRT Decoder가 예측한 컬러
이를 통해 Neural Field가 시점 에 따라 적절한 색상을 복원하도록 학습됩니다.
2. Diffusion Training Loss ()
SRT 출력(또는 중간 결과)을 Diffusion 모델에서 노이즈 제거하도록 학습할 때 사용합니다.
타임스텝 , 노이즈 등에 대해
노이즈 예측 에러를 최소화합니다:
- : Diffusion U-Net이 예측하는 노이즈
- : 텍스트 조건 또는 추가적인 뷰 조건(있다면)
- : 시점 변환된 이미지(노이즈가 섞인 상태)
- : 앞서 SRT를 통해 얻은 장면 임베딩
- 이 손실을 통해 U-Net이 시점별 노이즈를 올바르게 제거하고 결과 이미지를 일관성 있게 복원하게 됩니다.
상세 흐름
- 입력 이미지를 SRT Encoder로 처리
- 여러 장의 2D 이미지를 카메라 포즈와 함께 인코딩 → 공통 장면 임베딩
- SRT Decoder로 새로운 시점 에 대한 색상 추론
- 광선(ray) 단위로 질의(쿼리)하는 구조
- 여기서 Epipolar Attention 같은 메커니즘을 사용해,
레이 간 기하학적 연관성(에피폴라 기하)을 반영
- Diffusion U-Net
- SRT Decoder가 예측한 부분 또는 중간 결과 이미지를 받아,
- 노이즈 제거 과정을 수행 → 결과 이미지를 더욱 정교화
- 최종 출력
- Denoised Outputs:
합성된 새로운 시점 이미지가 깨끗하게 복원됨 - 다양한 각도에서 일관성 있게 보기 가능
- Denoised Outputs:
요약
- SRT(Set Representation + Ray-based Decoder)
- 적은 수의 입력 뷰로부터,
- 장면 임베딩 를 학습해 다양한 시점으로 색상 예측을 수행
- View-conditioned Diffusion 모델
- SRT의 중간 결과를 노이즈 제거하면서
- 고품질로 기하학적 일관성(Geometry-aware)을 유지하는 출력을 생성
- : Ray별 색상 재현성
- : 시점 변환된 이미지에 대한 노이즈 제거 학습
- 결과적으로, 단일/소수 뷰만으로도 3D 장면을 일관성 있게 렌더링하고 Diffusion으로 세부 품질까지 높이는 Consistent 1-to-3 파이프라인을 구현합니다.
10. Image Restoration
Image degradation encompasses various factors that introduce imperfections to the original image, including Noise, Blur, JPEG compression, Color Distortion, and more.
Why Image Restoration is necessary?
- Image restoration can be used to enhance them back to their original quality.
- • Legal Evidence and Investigation: In criminal investigations or case inquiries, damaged images can be restored to secure and analyze crucial evidence
10.1 Cascaded Diffusion Models for High Fidelity Image Generation
Diffusion모델을 활용하여 resolution 을 한 모델
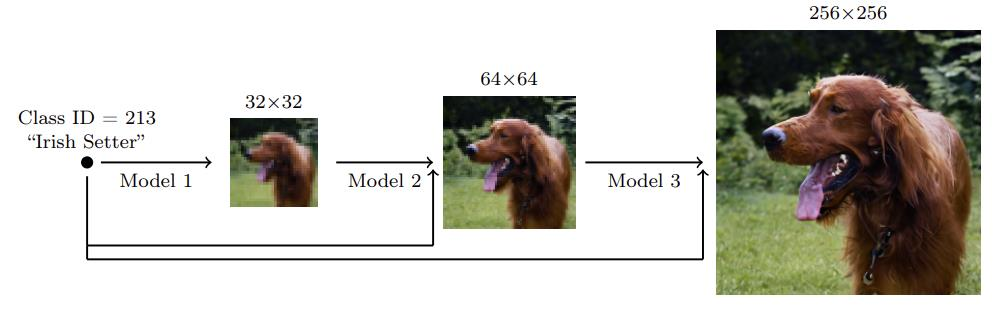
Method
이 연구에서는 Diffusion Model을 이용해 저해상도에서 고해상도로 점진적으로 이미지를 생성하는 계단식(또는 단계적) 이미지 생성 방법을 제안한다. 구체적으로 다음과 같은 단계를 거친다.
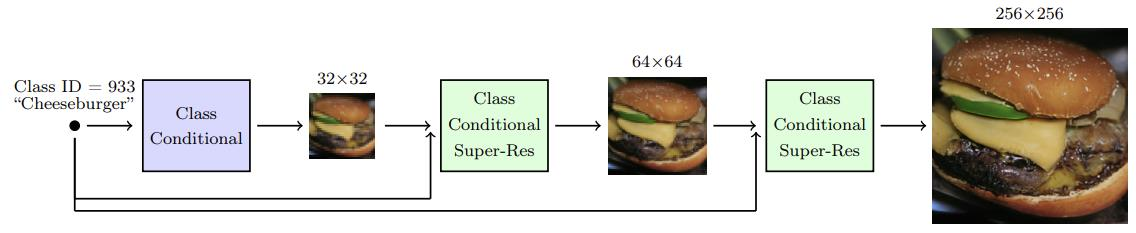
-
저해상도(Class-Conditional) 이미지 생성
- 먼저, 클래스 정보(예: 강아지, 치즈버거 등)를 조건으로 하는 Diffusion Model을 사용해 크기의 이미지를 생성한다.
- 이때 모델은 ‘어떤 클래스에 속하는 이미지인지’를 조건으로 받아 학습되어, 해당 클래스에 맞는 저해상도 이미지를 샘플링한다.
-
첫 번째 초해상화(Super-Resolution) 단계
- 생성된 이미지를 입력으로 받고, 동일한 클래스 정보를 함께 사용하는 초해상화 Diffusion Model을 통해 크기의 이미지로 해상도를 올린다.
- 이 모델 또한 클래스 정보를 사용하기 때문에, 단순히 픽셀 해상도만 높이는 것이 아니라 해당 클래스에 더 적합한 디테일을 보강한다.
-
두 번째 초해상화(Super-Resolution) 단계
- 앞 단계에서 생성된 이미지를 입력으로 다시 한 번 클래스 정보를 조건으로 하는 초해상화 Diffusion Model을 이용한다.
- 여기서 최종적으로 또는 그 이상의 목표 해상도까지 이미지 해상도를 높인다.
요약
- 클래스 정보를 조건으로 한 Diffusion Model로 저해상도 이미지를 먼저 생성한다.
- 이후 해상도를 점진적으로 높이는 초해상화 Diffusion Model들을 순차적으로 거치면서 고해상도 이미지를 얻는다.
- 이런 계단식 접근을 통해, 한 번에 고해상도를 직접 생성하는 것보다 안정적이고 세밀한 이미지를 생성할 수 있다.
10.2 DiffBIR: Towards Blind Image Restoration with Generative Diffusion Prior
motivation :
in the real world, many issues involve damage or problems that are not initially known or understood.
이 논문은 Blind Image Restoration 문제를 다룬다.
Blind Image Restoration이란, 이미지에 어떤 형태의 열화(노이즈, 블러, 저해상도 등)가 발생했는지 명시적으로 알지 못하는 상태에서 원본 이미지를 복원하는 과정을 말한다.

전체 구조 요약
모델은 크게 Stage 1과 Stage 2로 나뉜다.
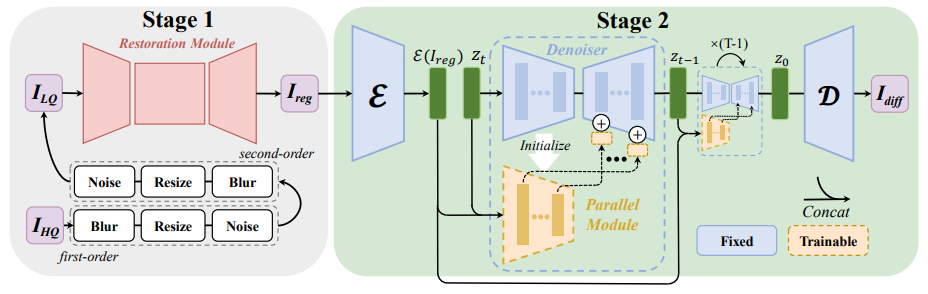
-
Stage 1: SwinIR을 통한 초기 복원
- 입력으로 저해상도이자 열화가 심한 이미지 가 들어온다.
- SwinIR 기반 Restoration Module을 통해 노이즈, 블러 등을 1차적으로 제거하여 비교적 깔끔한 중간 복원 이미지 를 얻는다.
-
Stage 2: Stable Diffusion을 통한 최종 복원
- 이미지를 Diffusion Model의 입력으로 사용한다.
- 우선 Encoder 를 통해 를 잠재 벡터 로 변환한다.
- Denoiser(Stable Diffusion)와 Parallel Module이 협력하여 반복적으로 과정을 거치며 열화 요소를 제거하고, 정교한 디테일을 복원한다.
- 마지막으로 Decoder 를 통해 를 최종 복원 이미지 로 디코딩한다.
세부 단계
Stage 1: SwinIR 복원 모듈
- 입력 이미지 는 노이즈, 블러 등으로 심각하게 열화되어 있다.
- SwinIR 기반 복원 모듈은 기존에 제안된 Vision Transformer 구조(Swin Transformer)를 활용하여,
- 저해상도 이미지의 특징을 추출하고
- 업샘플링과 함께 노이즈, 블러 등을 제거하면서
- 라는 중간 수준 해상도의 이미지를 생성한다.
Stage 2: Stable Diffusion
- 중간 복원 이미지 를 Encoder 를 통해 잠재 공간으로 보낸다.
- 여기서 얻어진 잠재 벡터 는 Diffusion 과정에서 반복적으로 변형된다.
- Denoiser는 각 시간 스텝별로 노이즈를 제거하고, Parallel Module을 통해 초기화 및 추가 정보를 제공받아 복원을 향상시킨다.
- 반복된 노이즈 제거 과정을 거쳐 최종 잠재 벡터 를 획득한다.
- Decoder 를 통해 가 다시 이미지 공간으로 변환되어 최종 복원된 이미지 를 얻는다.
결론
- Stage 1에서 SwinIR로 간단한 열화 요소를 먼저 제거하고,
- Stage 2에서 Stable Diffusion 기반 Denoiser로 복잡한 열화까지 정교하게 제거하면서
- 결과적으로 고품질 이미지를 복원해낸다.
이 과정을 통해, 기존 Blind Image Restoration 기법보다 풍부한 디테일과 높은 시각적 품질을 달성할 수 있다.
🤔SwinIR(ImageRestoration)은 무엇인가?
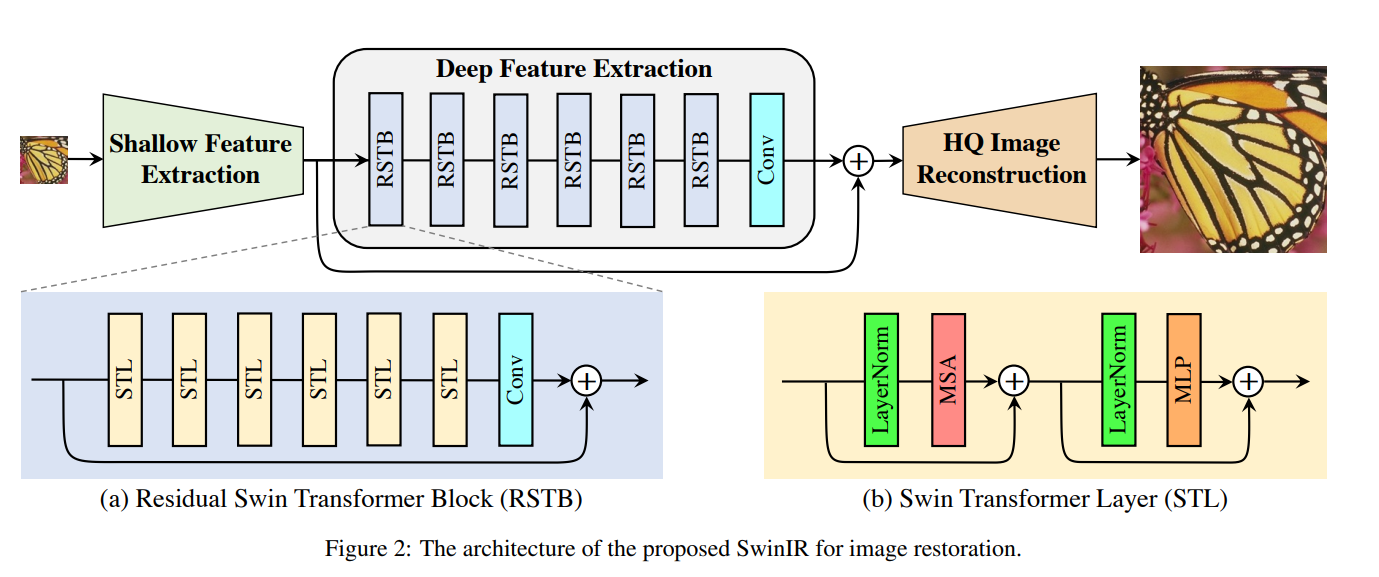
SwinIR은 크게 세 가지 모듈로 구성된다:
1) Shallow Feature Extraction
2) Deep Feature Extraction
3) High-Quality (HQ) Image Reconstruction
우리는 모든 복원(task)에서 동일한 특성 추출 모듈(Shallow/Deep Feature Extraction)을 사용하지만,
복원 유형(초해상화, 노이즈 제거 등)에 따라 다른 Reconstruction 모듈을 사용한다.
Shallow and Deep Feature Extraction
-
입력
- 저화질(LQ) 입력 이 주어진다. (여기서 , , 은 각각 영상의 높이, 폭, 채널 수를 의미)
-
Shallow Feature Extraction
- 먼저 컨볼루션 레이어 을 이용해 얕은 특성(shallow feature) 를 추출한다.
- 이는 다음과 같이 표현된다. 여기서 는 특성(feature) 채널 수이다.
- 초기 단계에서 컨볼루션 레이어를 사용하는 것은 시각적 특성 추출에 유리하며, 입력 이미지 공간을 고차원 특성 공간으로 매핑할 수 있는 단순한 방법을 제공한다.
-
Deep Feature Extraction
- 이어서, 로부터 깊은 특성 를 추출한다.
- 이 과정은 개의 Residual Swin Transformer Block(RSTB)과 하나의 컨볼루션 레이어로 구성된 모듈 을 통해 이루어지며,
- 구체적으로, 로 중간 특성 를 거쳐,로 최종 깊은 특성을 얻게 된다.
- 마지막에 컨볼루션 레이어()를 배치해 두어, Transformer 기반 네트워크에 컨볼루션의 Inductive Bias를 도입함으로써 특성 융합을 강화한다.
Image Reconstruction
-
초해상도(Super-Resolution) 예시
- 얕은 특성 와 깊은 특성 를 합하여 고화질(HQ) 영상 를 재구성한다. 여기서 은 재구성 모듈이다.
- 얕은 특성은 주로 저주파(low-frequency) 성분을, 깊은 특성은 고주파(high-frequency) 성분을 담당한다.
- 롱 스킵 커넥션(long skip connection)으로 인해, 저주파 정보()가 직접 재구성 모듈로 전달되어 고주파 정보 복원에 집중할 수 있도록 돕고, 학습 안정성도 높인다.
- 초해상도 작업 시에는 Sub-pixel Convolution Layer를 사용해 업샘플링을 수행한다.
- 얕은 특성 와 깊은 특성 를 합하여 고화질(HQ) 영상 를 재구성한다.
-
노이즈 제거, JPEG 압축 제거 등
- 업샘플링이 필요 없는 복원 작업에서는 단일 컨볼루션 레이어만으로 이미지를 복원한다.
- 또한, LQ 이미지와 복원 이미지의 잔차(residual)만을 재구성하도록 학습하여, 로 표현한다. 이 방식은 복원해야 할 부분만 집중적으로 학습하게 하여 효율적이다.
Loss Function
-
초해상도(SR)
- 다음과 같은 픽셀 손실을 최소화하도록 파라미터를 학습한다. 여기서 는 SwinIR의 출력이고, 는 정답(고화질 영상)이다.
- 고전적(Classical) / 경량(Lightweight) SR에서는 간단하게 픽셀 손실만 사용하는 경우가 많다.
- 실사(Real-World) SR에서는 시각적 품질 향상을 위해 픽셀 손실 + GAN 손실 + 퍼셉션 손실을 함께 사용하기도 한다.
- 다음과 같은 픽셀 손실을 최소화하도록 파라미터를 학습한다.
-
노이즈 제거, JPEG 압축 제거
- Charbonnier Loss를 사용한다. 여기서 은 일반적으로 정도로 설정한다.
- Charbonnier Loss를 사용한다.
Residual Swin Transformer Block (RSTB)
그림 2(a)에서 보이듯이, RSTB는 Swin Transformer Layers(STL)와 컨볼루션 레이어가 포함된 Residual Block 형태이다.
- 구조
- 번째 RSTB 입력 특성을 이라 할 때, 로 개의 Swin Transformer Layer(STL)를 거치며,
- 맨 뒤의 컨볼루션 레이어()는 Transformer의 공간가변(Spatially Varying) 특징과 컨볼루션의 공간불변(Spatially Invariant) 특징을 결합하여,
SwinIR의 Translational Equivariance를 보강해 준다. - Residual 연결을 통해 다양한 수준의 특성이 최종 재구성 모듈까지 전달될 수 있다.
- 번째 RSTB 입력 특성을 이라 할 때,
Swin Transformer Layer (STL)
-
기본 아이디어
- 원본 Transformer와 달리, Swin Transformer는 로컬 윈도우(Local Window) 기반의 Multi-Head Self-Attention(MSA)를 수행한다.
- 입력 크기가 라면, 이를 겹치지 않는 윈도우들로 나누고(총 개의 윈도우) 각 윈도우 단위로 자기어텐션을 적용한다.
-
계산 과정
- 한 윈도우의 특성 에 대하여, 로 를 만든 뒤,를 계산한다. (이 과정을 멀티 헤드(MHA)로 확장)
- 이후, LayerNorm과 MLP를 적용하고 Residual Connection을 더해,
- 한 윈도우의 특성 에 대하여,
-
Shifted Window Mechanism
- 윈도우 파티션이 고정되어 있으면, 각 윈도우 간 정보 교류가 어렵다.
- 그래서 정규 윈도우와 시프트 윈도우를 번갈아 가며 사용해, 서로 다른 윈도우가 겹쳐지는 영역을 형성, 크로스-윈도우 연산을 가능하게 한다.
이처럼 SwinIR은 Swin Transformer의 지역적 자가-어텐션을 활용해,
이미지 복원 작업(초해상도, 노이즈 제거, JPEG 압축 제거 등)에서 고품질 결과를 얻도록 설계되었다.
10.3 Solving Inverse Problem in Medical Imaging with Score-Based Generative Models
배경 (Background)
- 의료 영상 복원(Inverse Problem)
- 컴퓨터 단층촬영(CT)이나 자기 공명 영상(MRI)에서 원시(raw) 측정치(시노그램, k-스페이스 등)로부터 원본 영상을 복원하는 문제는 전형적인 역문제(Inverse Problem)이다.
- 기존 접근법: 지도 학습
- CT/MRI 이미지와 그에 대응되는 측정치(시노그램/ k-스페이스) 쌍을 대규모로 모아 지도 학습을 수행한다.
- 그러나 새로운 측정 과정(장비나 프로토콜이 다른 경우 등)에 대해서는 일반화가 어려운 문제가 있었다.
기여 (Contributions)
- Score-Based Generative Model을 의료 이미지의 사전 분포(Data Prior)로 활용하여 새로운 역문제 해결 방법을 제안한다.
- 이미지에 노이즈를 점진적으로 추가하고, 그 과정을 역으로 추적(Reverse SDE)하여 (Score Function)을 추정한다.
핵심 아이디어
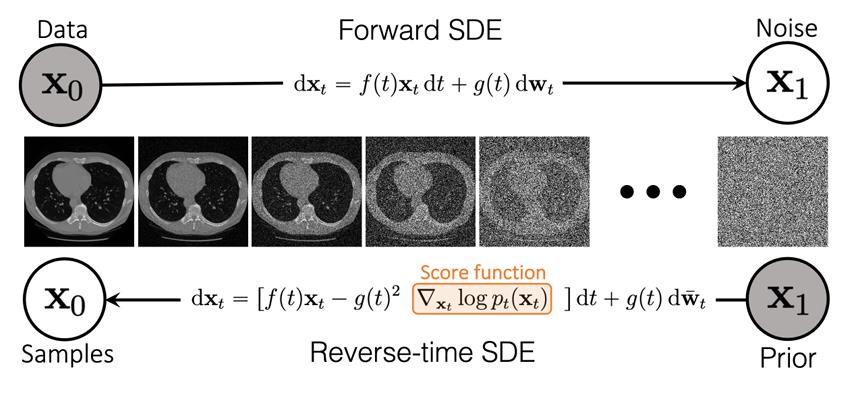
-
Score Function 추정
- 이미지 에 노이즈를 단계적으로 추가하여 로 만들고(Forward SDE),
- 에서 다시 노이즈를 제거(Reverse SDE)하는 과정을 통해 Score Function 을 추정한다.
- 이를 위해 훈련된 Score-Based Model 는 와 만을 입력으로 받아, 조건부가 아닌 무조건적(Unconditional) Score를 학습한다.
-
의료 영상에 적용
- 의료 영상(CT, MRI 등)에 대해 Score-Based Model을 학습함으로써, 의료 영상의 사전 분포를 모델링한다.
- 역문제(예: CT 재구성)에서 실제 측정치 가 주어지면,
- 분포와 결합하여 가 에 맞게 복원될 수 있도록 역방향 스텝을 진행한다.
-
조건부 Score Approximation
- 본래 조건부 Score Function 를 직접 추정하기 쉽지 않다.
- 따라서 무조건적 Score Function 와
- 측정 분포 를 적절히 결합하여, 의료 영상 복원을 수행한다.
-
의 확률 과정
- 측정치 에도 적절한 노이즈를 추가하여 로 만드는 확률 과정을 정의한다.
- 이를 통해 와 가 서로 일치하는 부분 정보를 유지하며,
- 중간 샘플들을 생성하고 반복적으로 업데이트하여 최종 복원 영상에 도달한다.
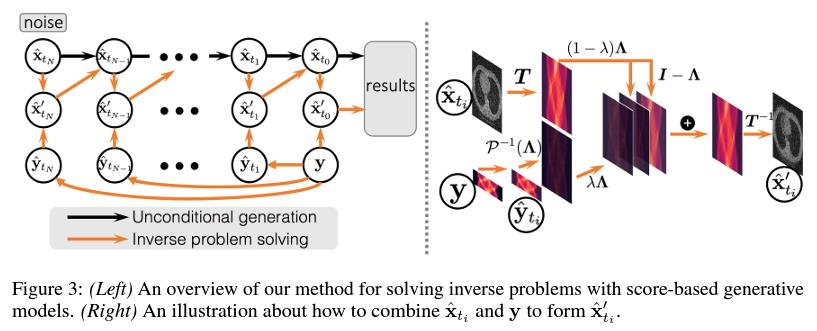
🚀 첫번째 이미지 수식을 좀더 풀어봅시다.
확률적 미분방정식(SDE)을 이용한 Score-Based Generative Model 개요
의료 영상(예: CT, MRI)을 고품질로 생성하거나 복원하기 위해, Score-Based Generative Model에서는 이미지를 점진적으로 노이즈화하는 Forward SDE와 이를 역으로 추적하는 Reverse SDE를 사용한다. 아래는 그 구조와 수식에 대한 좀 더 자세한 설명이다.
1. Forward SDE
개념
- Forward SDE(순방향 확률적 미분방정식)는 원본 이미지 를 점진적으로 노이즈화하여, 최종적으로 완전한 잡음 상태()까지 이르게 하는 확률 과정을 정의한다.
- 시간 동안, 는 다음 방정식을 따른다.
수식
(는 시점에서의 가 아주 짧은 시간 동안 변화하는 양(변화분)”을 의미)
- 여기서
- , : 시간에 따른 계수 함수
- : 표준 브라운 운동(또는 위너 프로세스)
- : 시간 에서의 랜덤 변수(이미지)
의미
- 항: 이미지 자체가 점진적으로 스케일링되거나 특정 Drift를 갖도록 만드는 항
- 항: 노이즈를 추가하는 항
- 에서는 가 깨끗한 원본 이미지 분포를 따르고,
- 에서는 이 거의 가우시안 잡음 분포에 근접하게 된다.
2. Reverse SDE
개념
- Reverse SDE(역방향 확률적 미분방정식)는 완전 잡음 상태()에서부터 점진적으로 노이즈를 제거하여 원본 이미지 분포()로 복원하기 위한 과정을 나타낸다.
- 이때 Score Function( )을 학습해서, 역방향 시점에서의 노이즈 제거 방향을 알려준다.
수식
- 주요 항목
- : 시간 에서의 이미지 분포 의 로그 확률에 대한 그래디언트(Score Function)
- : 역방향 브라운 운동(Forward SDE와 독립적이거나 적절히 정의된 프로세스)
의미
- 항: Forward SDE와 유사한 Drift 부분
- 항: 노이즈 제거를 수행하는 가장 핵심적인 부분
- 가 높을수록, 해당 가 이미지 분포에 더 적합하다는 뜻이므로, 그 방향으로 업데이트
- 결과적으로, 에서 거의 잡음뿐이었던 가 으로 갈수록 원본 이미지에 가까워짐
3. Score Function의 역할
정의
- Score Function:
- 이는 “현재 가 분포 상에서 얼마나 가능성이 큰 지점인지”를 나타내는 지표다.
학습 방식
- 이미지 에 노이즈를 점진적으로 주입(Forward SDE)
- 각 스텝별로 다양한 샘플을 얻는다.
- 신경망(Score-Based Model)이 , 만 입력받아 를 근사하도록 학습한다.
- 학습이 끝나면, 임의의 노이즈로부터 시작해서 역방향 SDE로 이미지를 샘플링하거나, 역문제 해석(예: 의료영상 복원)을 수행할 수 있다.
4. 의료 영상에서의 활용
-
학습 단계
- 대규모 의료 영상 데이터(CT, MRI 등)로부터 Score-Based Model을 학습한다.
- Forward SDE로 노이즈를 주입하고, 각 스텝별 와 사이를 학습.
-
샘플링/복원 단계
- Forward SDE의 거의 노이즈 상태(또는 실제 노이즈 상태)로부터 Reverse SDE를 통해 점진적으로 노이즈 제거
- 최종적으로 고품질의 의료 영상을 얻는다.
- 역문제(Inverse Problem)(예: CT나 MRI 재구성)에도 적용 가능
- 실제 측정 데이터(시노그램, k-space 등)를 조건으로 더 세밀하게 Score를 조정해가며 복원.
결론
- Score-Based Generative Model은 Forward/Reverse SDE를 통해 이미지 분포를 정교하게 학습하고,
- 의료 영상 등 고품질 복원이 필요한 영역에서 노이즈 제거나 재구성을 효과적으로 수행할 수 있다.
- 특히, Score Function을 잘 학습하면, 노이즈가 많이 섞인 상태에서도 실제 이미지 분포 방향으로 업데이트할 수 있어, 다양한 역문제 해결에 널리 활용될 전망이다.
정리
- 역문제(CT, MRI 재구성 등)를 해결하기 위해,
- 의료 영상을 대상으로 Score-Based Generative Model을 학습해 사전 분포를 얻는다.
- 측정치 를 노이즈 도입을 통해 확장한 뒤,
- Score Function과 역방향 확률 과정(Reverse SDE)을 결합하여 고품질 영상을 복원한다.
- 이는 기존에 데이터 쌍(이미지-측정치)에 의존하던 지도 학습 방식보다, 다양한 측정 환경에도 잘 일반화할 수 있는 장점을 가진다.
11. Other Applications
Beyond Generation, Diffusion models can be successfully applied to diverse vision tasks through their architecture, semantic features, diffusion process.
11.1 Label-Efficient Semantic Segmentation with Diffusion Models
Diffusion Model이 단순한 생성 모델이 아니라, 의미 있는 특징(semantic representation)을 학습하는 데에도 유리하다는 점을 실험적으로 입증하고 이를 레이블 효율적인 세그멘테이션에 적용하는 연구
Analysis
- UNet 디코더 중간 구간의 특성
- 역방향 확산(reverse diffusion) 과정에서 후반부 스텝에 해당하는 디코더 중간 블록들이 더 효율적으로 의미론적 정보를 포착한다.
- 블록 번호(Blocks numbering)
- 블록들은 딥(Deep)한 부분에서부터 얕은(Shallow) 부분 순으로 번호가 매겨진다.
- -means 클러스터링
- FFHQ 데이터셋에서 추출된 특성(feature)들을 기준으로 -means(클러스터 수 = 5)를 수행하면, 의미적으로 일관된 객체/객체-부위(Part)를 그룹화하는 클러스터들이 형성된다.

DDPM 기반 표현을 활용한 Few-shot 반지도 학습(세미-슈퍼바이즈) 세그멘테이션
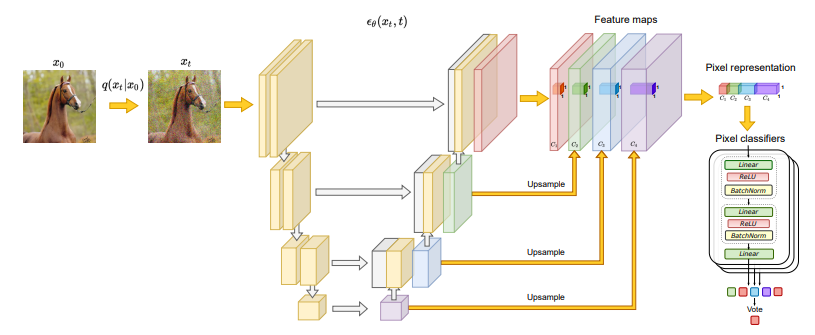
Label-efficient Semantic Segmentation with Diffusion Models: 구성도 상세 설명
위 그림은 Denoising Diffusion Probabilistic Model(DDPM) 또는 Score-Based Model에서 많이 사용하는 UNet 구조를 활용해 세그멘테이션에 필요한 픽셀 레벨 표현을 추출하는 과정을 보여준다.
이를 간단히 단계별로 살펴보면 다음과 같다.
1. 입력 데이터 준비
- 깨끗한 원본 이미지
- 세그멘테이션을 하고자 하는 이미지(예: 말 이미지를 예시로 듦).
- 노이즈를 추가한 이미지
- 원본 이미지 에 Forward Diffusion 과정을 통해 점진적으로 노이즈를 추가하여 얻은 .
이때, DDPM(또는 비슷한 확산 모델)은 를 입력으로 받아 노이즈를 제거하거나 이미지를 복원하는 구조로 설계된다.
2. UNet 구조로부터 특징 추출
그림에서 보이듯이, UNet은 인코더(Encoder)와 디코더(Decoder)로 나뉘며, 각 수준(level)에서 특징 맵(Feature Maps)을 추출한다.
-
인코더
- 입력 가 점차 Downsampling되면서 공간적 크기는 줄이고 특징 채널 수를 늘린다.
- 깊은 단계(Deep)로 갈수록 더 추상적인 특징을 포착한다.
-
디코더
- 인코더에서 추출된 정보를 활용해 Upsampling하면서, 다시 원본 해상도에 가까운 특징 맵을 복원한다.
- 역방향 확산(Reverse Diffusion) 과정을 수행할 때, 노이즈 제거 단계를 거치며 의미적 정보(semantic info)가 점차 드러난다.
-
Skip Connection
- 인코더의 특정 수준에서 추출된 특징을 디코더로 직접 전달해 준다.
- 이로 인해, 저수준(low-level) 정보와 고수준(high-level) 정보가 잘 결합되면서 복원이 정교해진다.
3. Feature Maps의 Upsampling & Pixel Representation
- 그림 오른쪽 부분에 보이는 Feature maps(빨간색, 녹색, 파란색, 보라색 박스 등)는 각각 UNet 디코더의 서로 다른 수준(block)에서 추출된 특징 맵이다.
- 이 Feature map들은 해상도가 서로 다를 수 있으므로, Upsample 과정을 통해 모두 동일한 해상도(일반적으로 원본 이미지 크기)로 맞춘다.
- 이후, 이 업샘플된 다중 수준의 특징 맵들을 Concatenate(연결) 하여, 각 픽셀 위치별로 하나의 긴 벡터를 형성한다.
- 예:
- (저해상도, 깊은 특징)
- (중간 해상도, 중간 수준 특징)
- (원본 해상도에 가까운 얕은 수준 특징)
- 이들을 Upsample → → 픽셀 단위로 묶어서 형태의 표현을 만든다.
- 예:
결과적으로, 픽셀마다 “(딥~얕은 수준) 특징들을 합친 벡터”가 만들어지는 셈이다.
4. Pixel Classifiers (MLP 앙상블)
- 이렇게 얻은 픽셀 단위 표현(예: )은 MLP(다층 퍼셉트론) 분류기에 입력된다.
- 그림 맨 오른쪽의 Pixel classifiers는, 예컨대:
- Linear + ReLU + BatchNorm
- Linear + ReLU + BatchNorm
- Linear
와 같은 간단한 계층으로 구성된 MLP 여러 개(앙상블)를 가리킨다.
- 각 픽셀이 “어떤 클래스에 해당하는지”를 확률적으로 예측한다.
- 앙상블 예측을 투표(vote) 방식으로 합쳐 최종 분류 결과(세그멘테이션)를 얻는다.
요약
- 노이즈를 추가한 입력()을 UNet에 통과시키면서, 다양한 해상도의 특징 맵을 추출한다.
- 각 해상도별 특징 맵을 업샘플링 후, 픽셀 단위로 연결해 최종 픽셀 벡터 표현을 만든다.
- 이를 MLP 분류기(여러 개의 작은 분류기로 이루어진 앙상블)에 입력해, 픽셀마다 세그멘테이션 라벨을 예측한다.
- 라벨이 적어도, DDPM을 통해 학습된 표현 덕분에 높은 성능을 낼 수 있다.
-
Unsupervised 학습으로 Diffusion Model 훈련
- 라벨 없는 이미지들에 대해서 DDPM(Denoising Diffusion Probabilistic Model)을 학습해 영상 분포를 모델링한다.
-
라벨이 있는 이미지에서 특성 벡터 추출
- 학습된 Diffusion Model(특히 UNet 구조)에서 추출된 표현들을 업샘플링 및 연결(concatenate) 하여, 각 라벨이 있는 이미지의 픽셀별 특성 벡터를 형성한다.
-
픽셀 레벨 분류기(MLP) 학습
- 위 단계에서 얻은 픽셀 특성 벡터를 입력으로 하는 독립적인 MLP 분류기들(앙상블)을 학습한다.
- 이 MLP들은 각 픽셀에 대해 의미론적 라벨을 예측하도록 학습되며, 소수의 라벨 정보만으로도 효과적인 세그멘테이션을 수행할 수 있게 된다.
11.2 ODISE: Open-Vocabulary Panoptic Segmentation with Text-to-Image Diffusion Models
대규모 텍스트-이미지 디퓨전 모델 + 디스크리미네이티브 모델을 결합해 어떤 카테고리라도(“in the wild”) 파놉틱 세그멘테이션을 수행 가능하게 함.
대규모 텍스트-이미지 디퓨전 모델을 오픈 어휘 세그멘테이션에 활용한 첫 연구.
즉, “텍스트-이미지 생성” 단계의 풍부한 표현력을 파놉틱 세그멘테이션에도 적극적으로 활용하는 프레임워크를 제안.
Method(Training Pipeline)
아래 그림은 ODISE에서 제안한 오픈-보캐뷸러리(열린 어휘) 파노픽 세그멘테이션 방법의 훈련 파이프라인을 나타낸다.
즉, 텍스트-투-이미지(Text-to-Image) 확산 모델(디퓨전 모델)을 활용하여, 사전에 정의되지 않은 새로운 카테고리 이름(어휘)도 처리할 수 있는 파노픽 세그멘테이션을 수행한다.
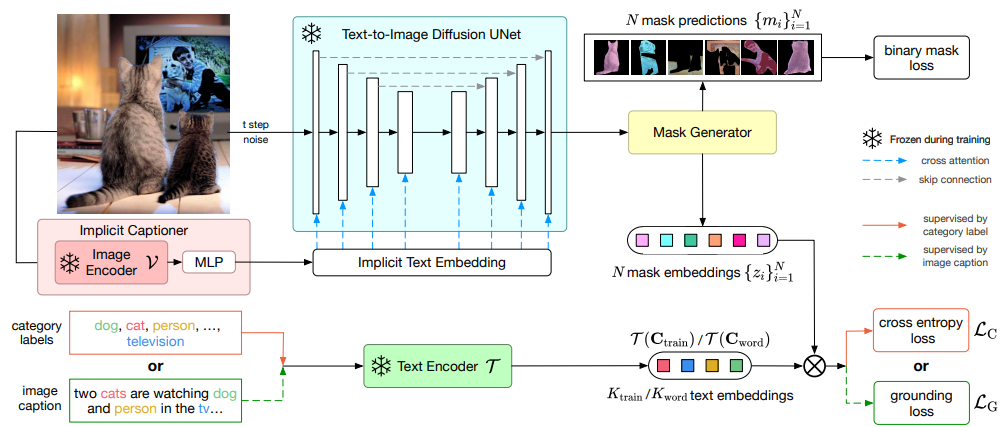
1. Implicit Captioner (이미지 캡션 생성)
- 이미지 인코더(예: CNN, ViT 등)로 입력 이미지를 임베딩(embedding)한다.
- MLP를 통해 이 임베딩에서 묵시적 캡션(Implicit Caption)을 생성한다.
- 이는 텍스트-투-이미지 Diffusion UNet이 사용할 텍스트 임베딩과 관련된 정보로, 학습 과정에서 동결(Frozen)되지 않고 공동 학습될 수 있다.
2. Text-to-Image Diffusion UNet
- 노이즈가 추가된 이미지 (시간 스텝 에서의 이미지)와
- Implicit Text Embedding(Implicit Captioner에서 나온 텍스트 임베딩)을 입력으로 받아,
- UNet 구조를 통해 노이즈 제거(reverse diffusion) 과정을 수행한다.
- 이때 크로스 어텐션(Cross Attention)이 텍스트 임베딩과 UNet의 중간 표현을 연결해 준다.
- Skip Connection 등은 그림에서 점선으로 표시.
- 여기서 UNet은 훈련 시에 동결(Frozen) 상태로 유지되어, 원본 텍스트-투-이미지 모델의 표현력을 최대한 활용한다.
3. Mask Generator (마스크 생성기)
- UNet의 출력 단계를 통해 개의 마스크 예측 을 만들어 낸다.
- 예: 사람, 고양이, TV 등 객체 영역을 각각 다른 마스크로 분리.
- 이때 각 마스크는 이진(Binary) 형태로 나오므로, Binary Mask Loss를 통해 감독(supervision)을 받는다.
추가로, 마스크에서 Pixel-level Feature를 추출하고, 이를 기반으로 개의 마스크 임베딩 을 형성한다.
- 즉, 각 마스크(객체 후보)에 대응하는 하나의 특징 벡터를 얻어냄.
4. Text Encoder (T) & Category / Caption Supervison
- 라벨된 카테고리(예: dog, cat, person 등) 혹은 이미지 캡션(예: "two cats are watching dog and person in the tv")을 텍스트 인코더 에 입력한다.
- 텍스트 인코더는 해당 문장을 텍스트 임베딩(문장 벡터)으로 변환한다.
(1) Category Label Supervision
- 만약 범주 라벨(category labels)이 있다면,
- 카테고리별 텍스트 임베딩 를 얻는다.
- 얻어진 임베딩과 마스크 임베딩 간의 상호작용(예: 내적 )을 통해 크로스 엔트로피 손실 를 계산한다.
- 이는 객체 분류 역할을 수행하여, 각 마스크가 어떤 범주에 속하는지 학습한다.
(2) Caption Supervision
- 만약 이미지 캡션이 주어진 경우,
- 텍스트 인코더 를 통해 캡션 임베딩을 추출한다.
- 마스크 임베딩과의 상호작용으로 그라운딩 손실 를 정의하고,
- 마스크가 캡션 내 특정 단어(또는 구)와 매칭되도록(그라운딩) 학습한다.
5. 손실 함수 요약
- Binary Mask Loss: 마스크 예측이 실제 객체/배경 영역을 잘 분리하는지 평가.
- Cross Entropy Loss(): 범주 라벨이 있는 경우, 카테고리 임베딩과 마스크 임베딩을 매칭함으로써 객체 분류를 학습.
- Grounding Loss(): 캡션 기반 그라운딩(어떤 단어가 어떤 객체를 가리키는지)을 학습.
이 모든 과정을 통해, 기존의 텍스트-투-이미지 모델(UNet)은 오픈 집합(미리 정의되지 않은) 범주까지 다룰 수 있는 파노픽 세그멘테이션 모델로 확장된다.
6. 핵심 요약
- Implicit Captioner → 이미지에서 내부적으로 텍스트 임베딩 생성
- Text-to-Image Diffusion UNet (Frozen) → 마스크 예측과 중간 표현 추출
- Mask Generator → 개의 마스크 & 마스크 임베딩 획득
- Text Encoder → 범주 라벨/캡션을 임베딩화 → 마스크 임베딩과 매칭
- Losses → Binary Mask Loss + Cross Entropy Loss() or Grounding Loss()
이를 통해, 오픈 어휘(Open-Vocabulary) 환경에서도 파노픽 세그멘테이션을 성공적으로 수행할 수 있다.
Method(Inference)
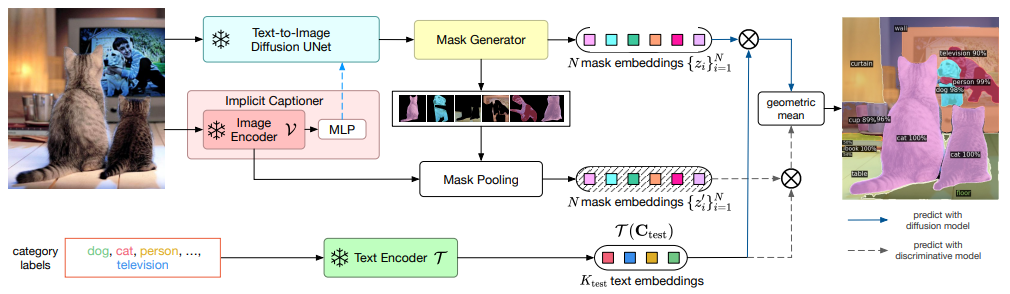
1) Implicit Captioner: 입력 이미지를 Image Encoder로 임베딩한 후, MLP를 통해 “암묵적 텍스트 임베딩”을 생성한다.
2) Diffusion UNet & Mask Generator: 텍스트 임베딩과 함께 UNet을 거쳐 여러 객체 마스크(및 해당 임베딩)를 예측한다.
3) Mask Pooling: 다른 모달리티(또는 추가 정보)에서 나온 마스크 임베딩과 합쳐, 각 마스크의 표현을 풍부하게 만든다.
4) Text Encoder: “cat”, “dog”, “person” 등 원하는 카테고리 이름을 텍스트 임베딩으로 변환한다.
5) Matching & Geometric Mean: 마스크 임베딩과 텍스트 임베딩 간의 내적 점수를 바탕으로, 최종 카테고리(또는 배경)를 결정한다.
11.3 Your Diffusion Model is secretly a zero-shot classifier
Background & Contribution
Diffusion 모델은 주로 콘텐츠 생성에 초점이 맞춰져 있으며, 판별 작업에는 덜 활용됩니다.
생성 모델을 판별 작업에 직접 활용하는 연구는 상대적으로 부족한 상황입니다.
- Diffusion Classifier는 텍스트-이미지 Diffusion 모델의 밀도 추정값을 활용해 추가 학습 없이 분류 작업에 적용합니다.
- 기존 판별 접근법보다 다중 모달 구성 추론 능력이 뛰어납니다.
Method
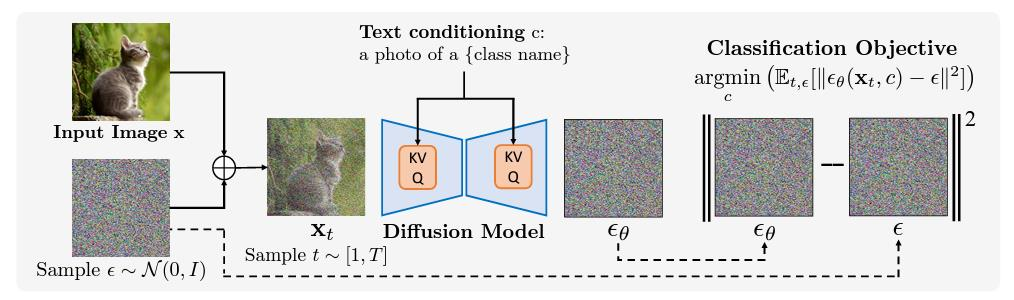
이 그림은 이미지 분류(classification)를 Diffusion 모델 관점에서 해석하는 과정을 보여줍니다.
주어진 이미지 에 노이즈 을 섞어 만든 를 텍스트 조건 (예: "a photo of a {class name}")와 함께
Diffusion 모델에 입력하고, 모델이 예측한 노이즈 와 실제 노이즈 간의 오차를 측정합니다.
가장 오차가 작은 텍스트 조건 가 입력 이미지의 클래스가 된다는 아이디어입니다.
1. 노이즈 추가 및 모델 예측
-
노이즈 샘플링
- 무작위 노이즈를 이미지에 추가해 노이즈 섞인 이미지 를 생성
-
Diffusion 모델 + 텍스트 조건
- 와 텍스트 조건 ("a photo of a cat" 등)를 모델에 입력
- 모델은 형태로 노이즈를 예측
2. 손실 함수 (Classification Objective)
모델이 출력한 노이즈 예측 와
실제 노이즈 의 차이(MSE)를 최소화합니다.
즉,
- : Diffusion 타임스텝(1부터 까지 균일 샘플)
- : 가우시안 노이즈
- : 시점 에서 노이즈가 섞인 상태의 이미지
- : 텍스트 조건 (이 경우, 후보 클래스 이름을 텍스트로 표현)
3. 개념적 해석
- 만약 가 정확한 클래스를 지칭한다면,
모델은 로부터 정확한 노이즈()를 잘 예측하게 되어,
값이 작아짐 - 반대로 잘못된 클래스일 경우,
모델이 예측한 노이즈가 실제 과 크게 달라져, 오차가 커짐 - 따라서 오차가 최소화되는 텍스트 가 이미지의 실제 클래스로 판정 가능
4. 흐름 요약
- 이미지
- 분류하고자 하는 입력
- 노이즈 추가 →
- 랜덤 노이즈 추가 후, 단계에 해당하는 생성
- Diffusion 모델
- 와 텍스트 조건 ("a photo of a cat" 등)을 입력받아
- 노이즈 예측
- 오차 계산
- 실제 노이즈 과의 차이
- 클래스 선택
- 여러 후보 중, 오차의 기댓값이 가장 작은 를 선택
- 즉,
이 과정을 통해, Diffusion 모델이 “가장 잘 설명되는 텍스트 조건”을 찾아내고,
이는 곧 이미지 분류(어떤 클래스인지)를 결정하는 결과가 됩니다.
Diffusion Classifier Algorithm

이 알고리즘은 분류(classification)를 위해 Diffusion 모델의 노이즈 예측 능력을 활용하는 기법을 요약한 것입니다.
각 클래스별(condition)로 노이즈 예측 오차를 측정하고, 그 오차가 가장 작은 클래스를 최종 분류 결과로 결정합니다.
의사 코드 (Pseudocode)
-
Input:
- 테스트할 이미지
- 분류 후보(조건) (예: 텍스트 임베딩 등)
- 각 입력당 반복(실험) 횟수
-
초기화
Errors[c_i]를 빈 리스트로 생성 (각 클래스 후보 마다)
-
Main Loop
- for trial :
- 타임스텝 샘플링: (또는 )
- 노이즈 샘플링
-
- 여기서 는 Diffusion 일정(schedule)에 따른 누적 노이즈 스케일
- 각 클래스 후보 에 대해:
- 모델 노이즈 예측
- 예측 오차 계산
Errors[c_k]에 추가 (append)
- end for
- for trial :
-
결과 산출
- 각 클래스 후보 에 대해
Errors[c_i]의 평균을 구함 - 를 분류 결과로 결정
- 각 클래스 후보 에 대해
알고리즘 해석
-
Diffusion 스텝() & 노이즈() 추가
- 원본 이미지 에 확률적 노이즈 과정을 가해 를 생성
- Diffusion 모델이 “해당 시점()에서의 노이즈”를 얼마나 잘 예측하는지 평가
-
클래스별 조건
- 클래스 를 “이 이미지가 에 속한다”고 가정했을 때,
- 모델은 로부터 노이즈 을 얼마나 정확히 예측할 수 있는지 확인
- 예측 오차가 작으면, 가 일 가능성이 높다고 간주
-
여러 번 시도(회)
- 단일 샘플링으로 오차를 비교하면 분산이 클 수 있으므로,
- 여러 번 노이즈 & 타임스텝을 바꿔가며 평균 오차를 구함
- 평균 오차가 가장 작은 클래스가 최종 분류 결과
Variance Reduction 기법
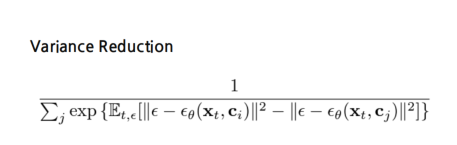
일반적으로, 각 클래스 마다 오차( )를 직접 추정하려면 샘플링이 많이 필요해 계산량이 부담될 수 있습니다.
따라서 “차이(difference in errors)만 추정”하는 식으로 개선할 수 있습니다.
예시: 차이 기반 기법
- 클래스별 절대적인 오차 대신 클래스 와 의 오차 차이를 추정함으로써
샘플링 수를 줄이고, 분산을 낮출 수 있음 - 최종적으로, 오차 차이가 최소인 클래스를 선택하면 성능은 같으면서도 샘플링 수가 감소하여 더 효율적인 계산 가능
요약
- Diffusion Classifier
- 원본 이미지 를 시점 에서 노이즈 추가 → 노이즈 예측 에러 측정
- 클래스별 노이즈 예측 성능 비교 → 오차가 최소인 클래스를 선택
- 장점
- 별도의 분류 헤드 없이, Diffusion 모델의 노이즈 예측 능력만으로 분류 가능
- 이미지→노이즈 재구성 과정을 통해 클래스 식별 수행
- Variance Reduction
- 전체 오차 대신 오차 차이만 추정하여 계산량 감소,
- 분산(variance)을 줄여 추정 안정성 상승
11.4 Emergent Correspondence from Image Diffusion
Background & Contribution
이미지 간 대응 관계를 찾는 것은 3D 복원, 객체 추적, 비디오 분할, 이미지 및 비디오 편집에 중요합니다. 그러나 이를 위해서는 명시적인 대응 레이블이 필요합니다.
- DIFT(Diffusion FeaTures)는 코사인 거리 기반의 최근접 이웃 탐색만으로 두 이미지의 대응 픽셀 위치를 찾아낼 수 있습니다. 이 방식은 다양한 카테고리와 이미지 형식에서도 강건하고 정확한 결과를 제공합니다. DIFT는 추가적인 미세 조정이나 감독 없이도 모든 작업에서 우수한 성능을 보여줍니다.
개념 요약
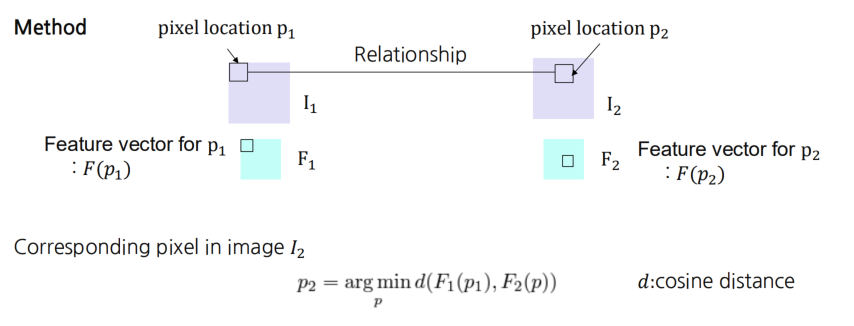
- 두 장의 이미지 가 있을 때,
- 특정 픽셀 위치 에 해당하는 특징 벡터 가 주어지고,
- 이 픽셀에 대응하는 위치 를 찾으려면,
내 모든 위치 에 대해서 특징 벡터 를 계산 후,
코사인 거리(cosine distance)를 최소화하는 위치 를 찾는다.
수식
여기서
- 는 cosine distance (또는 cosine similarity에 -1을 취한 값 등)를 뜻함.
Cosine Distance
코사인 거리는 일반적으로,
로 정의할 수 있으며,
와 가 유사(각도가 작음)할수록 는 작아집니다.
실제 절차
-
이미지 의 특정 픽셀
- 해당 위치에서 특징 벡터 추출
- 예: CNN의 중간 레이어 출력, 혹은 어떤 임베딩 모델 등을 통해
- 해당 위치에서 특징 벡터 추출
-
이미지 내 모든 위치 에 대해
- 특징 벡터 계산 (또는 미리 저장된 피처 맵에서 가져오기)
-
Cosine Distance 비교
- 를 구해, 가장 작은 를 로 결정
- 이는 이 가진 특징과 가장 유사한 특징(코사인 유사도가 가장 높은 위치)을 갖는 를 의미
-
결과
- 과 가 동일하거나 유사한 의미/객체/영역을 표현한다고 볼 수 있음
- 예: 서로 다른 시점의 영상에서 동일 객체나 대응점을 찾는 데 활용 가능
Diffusion Features (DIFT) Training
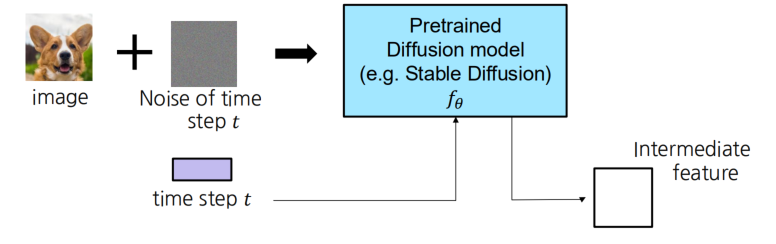
핵심 아이디어: 사전에 학습된 확산 모델(예: Stable Diffusion)을 활용해,
이미지에 시점 의 노이즈를 추가한 뒤 중간 레이어 특성(Intermediate Feature)을 추출하는 방법입니다.
과정 요약
-
이미지와 노이즈 결합
- 원본 이미지
- 노이즈 (시점 에 대응)
- 노이즈를 이미지에 섞어, 형태를 만듦
- : 시간 단계 에 따른 스케일링 파라미터
-
Pretrained Diffusion Model
- 사전 학습된 Stable Diffusion과 같은 모델 에
- 를 입력
- 시간 정보 가 조건(condition)으로도 함께 전달됨
-
중간 레이어 활성(Intermediate Feature) 추출
- 모델 내부에서 특정 레이어(예: U-Net 중간 레이어 등) 출력을 Feature로 받아옴
- 이를 Diffusion Feature(DIFT)라고 칭함
- 특징적으로, 시점 에 맞춰 노이즈가 섞인 상태의 이미지를 보고 학습된
Diffusion 모델의 표현 능력을 활용
수식으로 나타내기
-
노이즈 추가
여기서 는 누적 노이즈 스케줄 파라미터,
. -
모델 전파
- 입력:
- 출력: 중간 레이어에서의 Feature
-
목적
- 이렇게 뽑아낸 Feature가, 학습 분포(training distribution)에서 유의미한
표현 공간을 형성하도록 함 - 이후 다른 작업(분류, 회귀, 생성 등)을 위해 활용 가능
- 이렇게 뽑아낸 Feature가, 학습 분포(training distribution)에서 유의미한
요약
DIFT는 이미지와 노이즈를 결합해 생성된 특징 벡터를 기반으로, 사전 학습된 확산 모델에서 추출된 특징 공간에서 두 이미지의 유사한 위치를 대응 픽셀로 정합니다. 이 방식은 잡음과 변형에 강건하며, 이미지 정합, 3D 재구성 등 다양한 응용 분야에서 활용될 수 있습니다. 특징 공간 비교로 높은 표현력을 가지며 효율적인 계산 기법을 통해 성능을 향상시킬 수 있습니다.

11.5 AnoDDPM: Anomaly Detection with Denoising Diffusion Probabilistic Models using Simplex Noise
AnoDDPM은 DDPM(Denoising Diffusion Probabilistic Models)을 활용한 이상 탐지 기법을 제안합니다.
Background & Contribution
기존 생성 모델 기반 이상 탐지는 느린 추론 속도와 대규모 샘플에서의 불안정성 문제가 있었습니다.
AnoDDPM은 이상 이미지를 특정 시간 단계까지 노이즈를 추가하고 이를 복원해 건강한 근사 이미지를 생성합니다.특히 다중 스케일의 Simplex 노이즈를 활용해, 더 큰 이상 영역도 건강한 이미지로 복원할 수 있도록 설계되었습니다.이를 통해 효율적이고 안정적인 이상 탐지가 가능합니다.
Simplex Noise
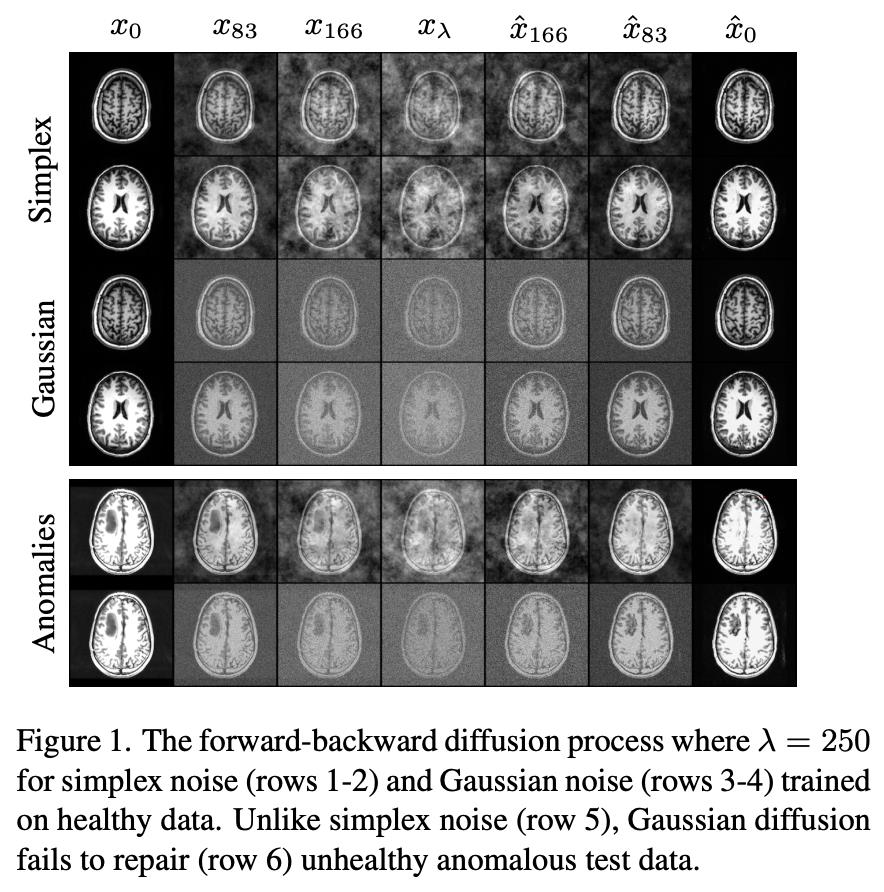
Simplex Noise는 Perlin Noise의 발전된 형태로, 주파수 분포를 보다 정밀하게 제어하며 부드럽고 구조화된 무작위성을 생성하는 알고리즘입니다.
일반적인 가우시안 노이즈와 달리, 특정 주파수 대역(스케일)에 대해 파워 로(power law) 형태를 따르는 스펙트럼을 구현할 수 있다는 점이 특징입니다.
1. 기본 아이디어
-
Perlin Noise의 단점을 보완
- Perlin Noise는 격자 기반으로, 차원이 높아질수록 계산량이 늘어납니다.
- Simplex Noise는 격자 대신 단순체(simplex, 삼각형/사면체 등)를 사용해
연산 효율과 품질을 모두 개선합니다.
-
주파수 분포 제어
- Simplex Noise를 여러 옥타브(octave)로 중첩해,
- 낮은 주파수부터 높은 주파수까지 적절히 가중합을 적용하면,
- 파워 법칙(power law)을 따르는 스펙트럼(에너지 분포)을 근사할 수 있습니다.
-
부드럽고 구조화된 랜덤 필드
- 가우시안 노이즈처럼 완전히 무작위 형태가 아니라,
- 연속성과 구조(smoothness)를 갖는 무작위 분포를 생성
- 예: 자연스러운 지형, 유기적 패턴 등 시뮬레이션에 유용
2. 간단한 수식 표현
단순화된 2D Simplex Noise 예시:
- : 좌표에 대해, 해당 단순체(삼각형) 내에서의 좌표 변환
- : 각 단순체에 할당된 그라디언트(Gradient) 기여
- : 옥타브별 가중치 (주파수/진폭 제어)
- : 옥타브(스케일) 수
이 과정을 통해, 여러 스케일에서 합성된 결과가 파워 로 분포를 가까이 모사할 수 있도록 설계할 수 있습니다.
3. 특징 및 장점
-
계산 효율
- Perlin Noise 대비 O(n)에서 O(2^n) 수준의 차이를 보이는 경우가 있음
- 차원이 올라갈수록 더 효과적
-
주파수 제어
- 하위 주파수(저주파)부터 고주파까지 옥타브를 중첩하며
- 암시적인 스펙트럼 형성 가능
- 자연스럽고 매끄러운 노이즈 패턴 생성에 적합
-
다양한 응용
- 컴퓨터 그래픽스(절차적 지형, 텍스처 생성)
- 시뮬레이션(유체, 연기, 날씨 패턴)
- 머신 러닝에서 특정 노이즈 스펙트럼을 필요로 할 때(위 그림처럼 의료 이미지를 세밀하게 노이즈화)
4. 예시: 파워 로 근사
파워 로(Power Law) 스펙트럼을 간단히 표현하면:
- $E(k $: 파워 스펙트럼(에너지),
- : 파장 수(주파수),
- : 기울기(파워 로 지수)
Simplex Noise에 옥타브를 여러 개 적용하면 각 옥타브에서 주파수 , 진폭 등을 조절하여 전체 합이 꼴의 분포를 가까이 따르도록 튜닝할 수 있습니다.
Algorithm 1: Training

- repeat
- 샘플링:
- : 원본 데이터에서 이미지 추출
- :
타임스텝 무작위 선택
- Simplex 시드 생성:
- 단순체 노이즈를 생성하기 위해, 파라미터 등을 지정
- 예:
- : 스케일, : 옥타브(스케일 단계) 수, : 가중치 등
- 노이즈 추가:
- 여기서 는 확산 스케줄에 따른 누적(variance) 항
- 오차 역전파
- 목적 함수를 로 두고,
- 에 대해 경사 하강(Gradient Descent) 업데이트
- 목적 함수를
- 샘플링:
- until converged
- 위 과정을 반복해 파라미터 (확산 모델)를 학습
- Simplex Noise가 이미지에 추가되어,
공간적·스펙트럼적 구조를 갖는 노이즈 상황을 모델이 잘 학습하게 됨
Algorithm 2: Inference (Segmentation 예시)

-
입력 및 초기화
- :
- 테스트(추론) 이미지 (예: A는 전처리/추가 조건 등)
- :
- 시점 에서 노이즈가 섞인 상태로 만들기 (시작점)
- :
-
Reverse Diffusion Loop
- for :
- Simplex Noise 추가
- if , else
- (즉, 일 때만 Simplex 노이즈 사용)
- Reverse update
- 여기서
- , 등은 확산 스케줄 관련 파라미터
- 는 학습된 확산 모델의 노이즈 예측
- : Simplex 노이즈 추가 항
- Simplex Noise 추가
- end for
- for :
-
Segmentation 결과
- 등
- 예를 들어, 복원된 이미지(또는 생성 결과)와 원본의 차이 등을 계산해
세그멘테이션 마스크를 얻거나, - 어떤 임계치 등을 넘어서면 마스크를 1(또는 0)로 설정
- 예를 들어, 복원된 이미지(또는 생성 결과)와 원본의 차이 등을 계산해
- return
- 등
핵심 해석
-
학습(Training)
- Simplex Noise를 사용해 주파수 스펙트럼이 제어된 노이즈를 이미지에 추가
- 모델이 이를 복원(또는 노이즈 예측)하도록 학습해 공간적 구조를 살린 노이즈 대응 능력을 얻음
-
추론(Inference)
- 거꾸로(Reverse) 확산 과정을 수행하며,
- Simplex Noise를 매 단계 inject함으로써
이미지 복원 또는 세그멘테이션 지표(오류)를 추출 - 최종적으로 가 세그멘테이션 결과를 나타내도록 설계할 수 있음
(예: 원본 대비 복원 에러 지도, 그 이상값이 객체 영역)
요약
- Algorithm 1 (Training):
- Simplex Noise로 생성한 을 이용해 이미지에 노이즈를 추가
- Diffusion 모델이 이 노이즈를 예측·제거하도록 학습
- Algorithm 2 (Inference: Segmentation):
- 테스트 이미지에 유사한 방식으로 Simplex Noise를 주입하며 역확산(reverse diffusion)
- 복원 과정에서 나온 에러() 등을 이용해 세그멘테이션을 수행
이를 통해, 가우시안 노이즈와 달리 다양한 주파수 구조를 가진 노이즈 상황에서도 Diffusion 모델을 학습·적용할 수 있으며, 특히 의료영상 등에서 구조적 이상 탐지나 정밀 세그멘테이션에 유리한 결과를 얻습니다.
