1. Unconditional Image Generation

Unconditional Generation 개요

Unconditional Generation이란, 사전에 주어진 레이블(label)이나 추가 조건 없이,
모델이 오직 데이터 분포만 학습하여 새로운 이미지를 생성하는 과정을 말합니다.

• 주요 목표: 기존에 존재하지 않던, 새롭고 독창적인 이미지를 만들어내는 것
• 예: 노이즈(무작위 벡터)를 입력으로 넣으면, Diffusion Model이나 GAN 등이 이를 이미지로 변환

이 방법은 데이터 분포를 온전히 모델링해야 하므로,
데이터의 통계적 특성을 이해하고 분포를 학습하는 데 유용합니다.

왜 Unconditional Generation이 중요한가?

1. 데이터 분포 학습

   • 모델이 다양한 샘플을 만들려면, 데이터가 지닌 특징·패턴·통계적 속성을 제대로 파악해야 함.
   • 이를 통해 내재적 구조를 이해하는 데 도움.

2. 광범위한 활용 가능성

   • 데이터 증강(새로운 예시 생성)
   • Representation 학습(잠재공간 이해)
   • Creative AI(예술 분야 등)

3. 다양한 분야에서 핵심적 역할

   • 다른 조건(레이블 등)이 필요 없어 간단하면서도,
   • 학습 안정성·생성 능력 등 여러 측면에서 연구가 활발.

1.1 DDPM(Denoising Diffusion Probabilistic Model)

Background

• 기존의 생성 모델들(GAN, Flow, VAE 등)은 성능이나 학습 안정성 면에서 일정 한계를 보였음.
• 저자들은 이러한 한계를 부분적으로 극복할 수 있는 새로운 생성 모델(Diffusion Model)을 제안함.

Contributions

1. 새로운 생성 모델을 제안
2. Diffusion 모델과 변분추론 사이의 연결고리를 찾아,
   • 마코프 체인 학습,
   • Denoising Score Matching,
   • Annealed Langevin Dynamics 등과 결합해 설명

1.1.1 Diffusion Models란?

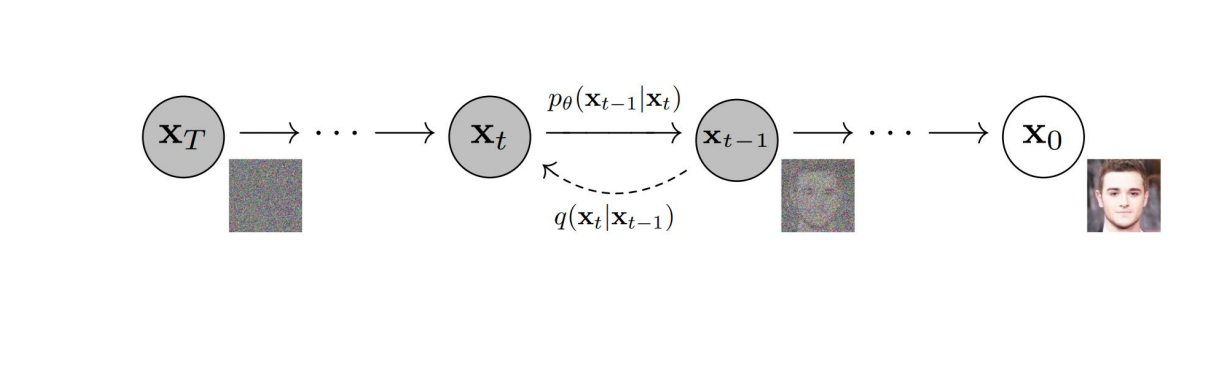
Diffusion Models는 이미지에 단계적으로 노이즈를 더했다가
그 노이즈를 제거해가는 방식으로 깨끗한 이미지를 재구성하는 모델입니다.

1. Forward 과정:

   • $x_0$ (원본 이미지)에서 시작해,
   • 점차 노이즈를 주입하여 $x_1, x_2, \dots, x_T$를 만듦.
   • 결국 $x_T$는 거의 완전한 노이즈 상태에 가까움.

2. Reverse 과정:

   • 학습된 파라미터 $\theta$를 사용해,
   • $x_T$에서부터 노이즈를 한 단계씩 제거($x_{T-1}, x_{T-2}, \dots$)해
   • 최종적으로 깨끗한 이미지 $x_0$를 복원.

이 과정을 통해, 무작위 노이즈에서 출발해도 그럴듯한 이미지를 생성 가능.

1.1.2 학습 방법: Noise 예측

Diffusion Model에서는 보통 수많은 시점($t$)을 상정하고,
각 시점마다 이미지에 섞인 노이즈를 예측하도록 학습합니다.

• 학습 손실 예시:

  $L_\text{simple}(\theta) := \mathbb{E}_{t, x_0, \epsilon} \bigl[ \bigl\| \epsilon - \epsilon_\theta\bigl(\sqrt{\overline{\alpha}_t}\,x_0 \;+\; \sqrt{1 - \overline{\alpha}_t}\,\epsilon,\;t\bigr) \bigr\|^2 \bigr].$
  • 여기서 $\epsilon$는 가우시안 노이즈
  • $\epsilon_\theta(\cdot)$는 모델이 예측하는 노이즈
  • $\overline{\alpha}_t$는 노이즈 스케줄에 따른 계수

• 이 손실을 최소화하면, 모델은 $x_t$에 포함된 노이즈($\epsilon$)를 정확히 추정하는 능력을 갖춤.

• 결과:

  • Reverse 단계에서 노이즈를 제거해,
  • 깨끗한 이미지를 복원할 수 있게 됨.

1.1.3 Sampling (샘플링) 절차

논문에서 보통 $T = 1000$(타임스텝)을 사용하며, 샘플링 절차는 다음과 같습니다:

1. 초기화:
   • $x_T \sim \mathcal{N}(0, \mathbf{I})$ (순수 노이즈)
2. Reverse 반복 (for $t = T, \dots, 1$):
   1. $z \sim \mathcal{N}(0, \mathbf{I})$ if $t > 1$, else $z = 0$
   2. $x_{t-1} = \frac{1}{\sqrt{\alpha_t}} \Bigl( x_t - \frac{1 - \alpha_t}{\sqrt{1 - \overline{\alpha}_t}}\,\epsilon_\theta(x_t, t) \Bigr) + \sigma_t \, z$
      (여기서 $\sigma_t$는 노이즈 스케줄에 따른 표준편차)
3. 반복 종료 후 $x_0$를 반환 → 완성된 이미지

• 이 과정을 통해, 무작위 가우시안 노이즈에서 시작해도 깨끗하고 사실적인 이미지를 얻을 수 있음.

요약

• Unconditional Generation:

  • 어떠한 조건 없이 데이터 분포만 학습하여, 새롭고 독창적인 이미지를 생성.
  • 데이터의 분포적 이해와 학습 능력을 시험하는 핵심적인 방법.

• Diffusion Models:

  • Forward (노이즈 주입) + Reverse (노이즈 제거) 과정을 통해 이미지 생성.
  • $T$단계로 분해해, 노이즈 예측을 학습하는 방식.
  • 학습된 모델은 Sampling 절차를 거쳐 노이즈 → 이미지 변환 가능.

• 이러한 접근은 기존 GAN/Flow/VAE의 한계를 어느 정도 보완하며,
  마코프 체인, Score Matching, Langevin Dynamics 등과 관련이 깊어
  다양한 연구로 확장되고 있습니다.

1.2 Improved Denoising Diffusion Probabilistic Model

배경

일반적인 DDPM(Denoising Diffusion Probabilistic Model)은 뛰어난 생성 성능을 보였지만 모델에 대한 상세 분석이나 다양한 구성 요소에 대한 정보가 부족했다. 이를 해결하기 위해 개선된 DDPM에서는 여러 가지 실험과 분석을 통해 모델 구조 학습 방식 노이즈 스케줄링 등 다양한 측면에서 성능 개선을 시도했다.

1. 기존 DDPM에서의 분산(고정)

DDPM에서 Reverse(생성) 과정은 보통 다음과 같은 형태의 확률 분포로 표현됩니다:

즉, $x_t$가 주어졌을 때 이전 시점 $x_{t-1}$의 분포를 가우시안으로 가정하고,
모델이 그 가우시안의 평균($\mu_\theta$)과 분산($\Sigma_\theta$)을 결정(혹은 예측)합니다.

기존 DDPM 논문(Ho et al., 2020)에서는 이 중 ‘분산(variance)’을 학습하지 않고,
고정된 값(forward process의 $\beta_t$나 특정 공식으로 유도된 값)으로 사용했습니다.

• 즉, 모델이 학습하는 항은 평균(노이즈 예측)뿐이고,
• 분산($\Sigma$)은 일정 스케줄대로 ‘고정(fixed)’되어 있었습니다.

2. 개선된 DDPM에서의 분산 학습

하지만 이후 개선된 DDPM(예: Nichol & Dhariwal, 2021 “Improved Denoising Diffusion Probabilistic Models”) 등에서는,
분산도 모델이 직접 추정하도록(혹은 일부 파라미터를 학습하도록) 바꿨습니다.

• 즉, $\Sigma_\theta(x_t, t)$를 “직접 모델이 예측”하게 만들어,
  Reverse 단계에서 더 정교한(맞춤형) 분포를 추정할 수 있게 된 것입니다.

이를 통해

1. 단순 고정 스케줄로는 잡아내지 못했던 미세한 부분을 더 잘 모델링
2. 그 결과 약간의 성능(샘플 품질) 향상 확인

이라는 장점이 보고되었습니다.

주요 실험 결과

1. 분산 학습($\Sigma_{\theta}(x_t, t)$)
   기존 DDPM에서는 분산을 고정된 값으로 설정했지만 개선된 DDPM에서는 분산을 직접 학습하도록 했다. 이를 통해 약간의 성능 향상이 확인되었다.

2. 확산 단계 수 증가
   기본 DDPM에서는 1000단계로 학습했지만 개선된 DDPM 연구에서는 4000단계까지 시도하여 성능이 더욱 향상되었음을 확인했다.

3. 노이즈 스케줄의 변경(선형에서 코사인으로)
   기존 DDPM은 선형적으로 노이즈를 증가시키는 스케줄을 사용했다. 하지만 마지막 단계에서 노이즈가 과도하게 누적되어 샘플 품질이 저하되는 문제가 있었다. 개선된 DDPM에서는 코사인 스케줄을 도입해 노이즈를 부드럽게 변화시켰고 그 결과 샘플의 품질이 개선되었다.

기여

• 모델이 학습해야 하는 항(variance 포함)에 관한 실험 및 분석을 수행했다.
• 확산 단계(step) 수의 변화에 따른 성능 변화를 조사했다.
• 노이즈 스케줄(schedule) 방식을 변경하여 샘플 품질에 미치는 영향을 검증했다.

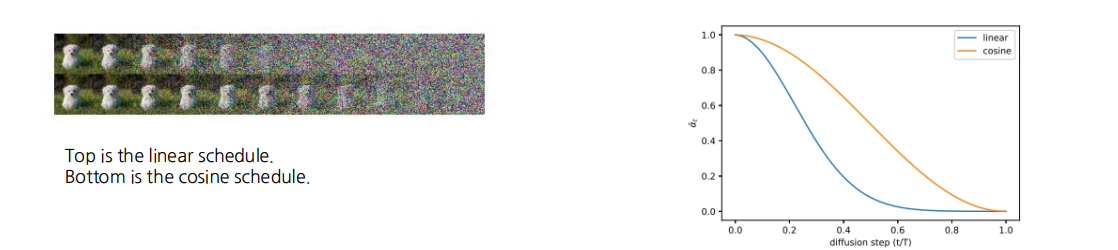
요약

개선된 DDPM에서는 고정되어 있던 분산을 학습 대상으로 바꾸고 확산 단계 수를 늘리며 노이즈 스케줄을 선형에서 코사인으로 변경하여 전반적인 샘플 품질과 모델 성능을 높였다.

1.3 High-Resolution Image Synthesis with Latent Diffusion Models

배경

• Diffusion 모델은 우수한 성능을 보였지만, 생성 과정 전체에서 해상도가 고정된다는 단점이 있었습니다. 이로 인해 계산 비용이 증가하고 처리 시간이 길어지는 문제가 발생했습니다.
• 예) 일반적인 Diffusion 모델은 단계별로 이미지를 변환할 때 동일 해상도를 유지해야 하므로, 고해상도 이미지를 직접 다룰 경우 연산량이 매우 커집니다.

Latent Diffusion Model의 주요 아이디어

• 잠재 공간으로의 매핑
  • 입력 이미지 x는 인코더 E를 통해 잠재 공간 z로 매핑됩니다. 이때 이미지의 해상도를 낮추어 표현하므로, 고해상도를 직접 다루는 대신 더 작은 공간에서 Diffusion 과정을 수행할 수 있습니다.
• Diffusion 과정
  • 잠재 공간에서 노이징과 디노이징을 반복하며 이미지 특징을 학습합니다.
  • 단계 T를 거치면서 z$T$ 형태로 노이징이 진행되고, Denoising U-Net $\epsilon_\theta$가 이를 점진적으로 복원합니다$z_{T-1}$ → $z_{T-2}$ → ... → z$0$.
• 디코더 D
  • 잠재 공간에서 최종적으로 복원된 $z_{0}$를 다시 픽셀 공간으로 되돌리는 역할을 합니다.
  • 즉, 인코더 E에서 축소된 이미지 표현을 사용해 Diffusion을 수행한 뒤, 최종 결과를 디코더 D로 복원해 고해상도 이미지를 얻습니다.

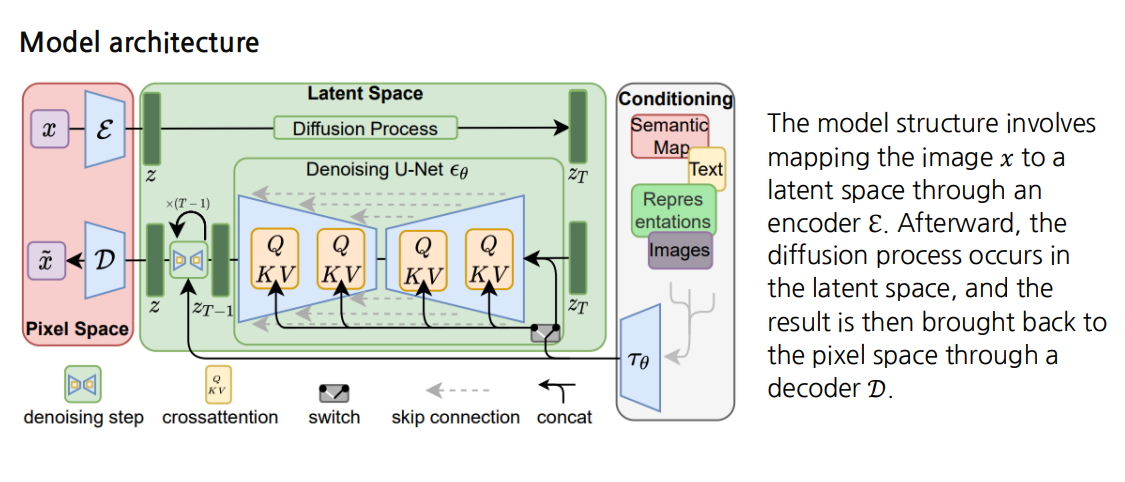
모델 구조

위 과정을 좀 더 구체적으로 살펴보면 다음과 같습니다.

1. 인코더 E

   • 원본 이미지 $x$를 받아 잠재 벡터 $z$로 변환합니다.
   • 이 때 해상도가 낮아지므로, 원본 이미지를 직접 다루는 것보다 연산량이 크게 절감됩니다.

2. Latent Space

   • 인코더 E가 출력한 z에 대해 Diffusion 과정을 수행합니다.
   • 이 공간은 잘 학습된 표현 공간으로, 고해상도를 그대로 유지하지 않아도 이미지를 효율적으로 재구성할 수 있습니다.

3. Denoising U-Net

   • Diffusion 과정에서 단계별로 노이즈가 추가된 z$T$를 점차 복원해 나가는 역할을 합니다.
   • Cross-attention 메커니즘을 이용해 다양한 형태$텍스트, 이미지, 시멘틱 맵 등$의 조건을 입력으로 받아 다중 모달 학습을 수행할 수 있습니다.

4. 디코더 D

   • 최종적으로 복원된 잠재 벡터 $z_0$를 다시 원본 해상도로 되돌립니다.
   • 이 결과물이 최종 고해상도 이미지 $\tilde{x}$가 됩니다.

주요 기여

1. 잠재 공간 사용으로 인한 계산 효율성 향상

   • 고해상도를 그대로 사용하는 대신, 압축된 잠재 공간에서 Diffusion을 진행하므로 큰 연산량과 메모리 사용량을 절감할 수 있습니다.

2. 범용 컨디셔닝 메커니즘

   • Cross-attention 기반으로 텍스트나 시멘틱 맵, 추가 이미지를 포함한 다양한 입력을 조건으로 사용할 수 있어, 다중 모달 학습과 생성이 가능합니다.

3. 다양한 태스크에서의 경쟁력 있는 성능

   • 무조건적 이미지 합성(unconditional image synthesis), 인페인팅(inpainting), 확률적 초해상도(stochastic super-resolution) 등 여러 과제에서 우수한 성능을 보여줍니다.

결론

Latent Diffusion Model은 기존 Diffusion 모델이 갖고 있던 고해상도 유지로 인한 연산 비용 증가 문제를 잠재 공간으로의 매핑인코더를 통해 해결합니다. 그리고 Cross-attention 기반 컨디셔닝으로 다양한 정보를 결합해, 여러 이미지 생성 태스크에서 고품질 결과를 달성합니다. 최종적으로 디코더 D를 통해 저해상도 잠재 공간에서 작업한 결과물을 다시 고해상도의 픽셀 공간으로 복원함으로써, 효율과 성능 모두를 얻을 수 있다는 점이 가장 큰 장점입니다.

2. Fast sampling

개요

Diffusion Models(DMs)은 높은 품질의 이미지를 생성할 수 있는 강력한 생성 모델입니다.
그러나 수백, 수천 단계에 달하는 느린 샘플링 과정 때문에 실용적으로 사용하기 어려운 문제가 있었습니다.
이로 인해 빠른 샘플링 기법(fast sampling techniques)이 다양한 연구자들에 의해 제안되고 있습니다

왜 Fast Sampling이 필요한가?

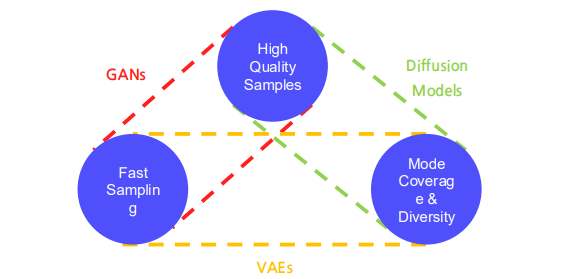
모델 유형	특징
GANs	매우 빠른 샘플링 속도
VAEs	빠른 샘플링과 안정된 학습
Diffusion Models	높은 품질의 샘플 + 모드 커버리지(다양성)

• Diffusion Models은 이미지를 비롯하여 음성(speech), 비디오(video) 등 다양한 분야에서 뛰어난 생성 품질을 보이지만,
• 학습 및 샘플링 과정이 느리고 비용이 많이 든다는 단점이 있습니다.
• 따라서, 빠른 샘플링 기법을 적용하면 효율적인 학습뿐 아니라 샘플링 속도도 크게 높일 수 있어 보다 폭넓은 응용이 가능해집니다.
  

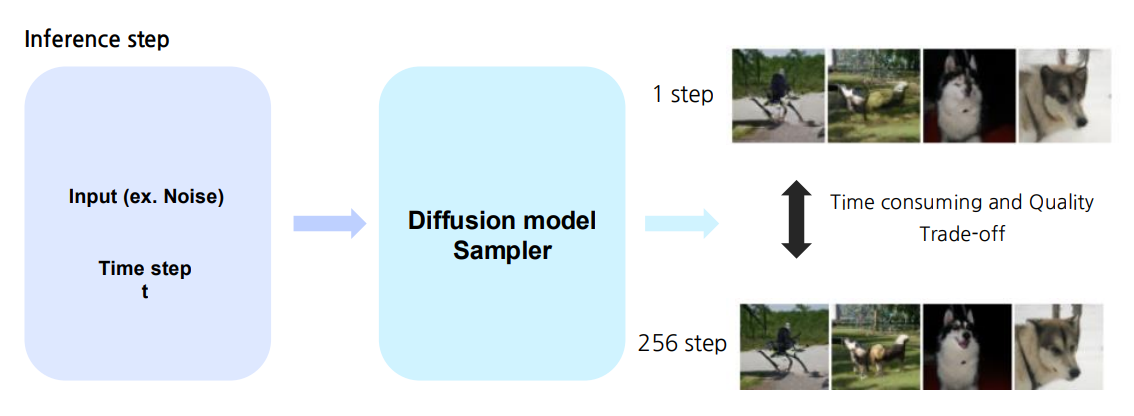
Fast Sampling의 목적

• 시간 단계(time steps) 수를 줄이면서도,
• 이미지 품질(혹은 다른 생성 결과 품질)의 저하를 최소화하는 것.

즉, 가능한 한 적은 추론 단계로도 원본에 가까운 높은 품질의 샘플을 얻고자 합니다.

Fast Sampling 기법의 분류

1. Training free sampler

   • 추가 학습 없이도 샘플링 단계를 줄일 수 있도록,
     SDE나 ODE 해석 관점에서 이산화(discretization) 단계를 줄이는 방식을 사용합니다.
   • 대표 예:
     • DDIM (Denoising Diffusion Implicit Models)
       • Diffusion 과정의 수식을 ODE 형태로 재해석해서, 시간 단계를 줄인 샘플링을 가능케 합니다.
       • 기존 DDPM 대비 추론 단계가 크게 단축되면서도, 품질 손실을 일정 부분 억제합니다.

2. Training based sampler

   • 빠른 샘플링을 위해 새로운 네트워크(서로게이트 네트워크)를 추가 학습시켜,
     수치 해석 과정 일부 또는 전부를 대체하는 방법입니다.
   • 대표 예:
     • Progressive distillation for fast sampling of diffusion models
       • 모델을 distillation하는 과정을 통해
         추론 단계를 반복적으로 절반씩 줄여나가는 기법을 제안합니다.
       • 원래 수백 단계가 필요한 샘플링을 훨씬 줄이면서도
         품질 저하를 최소화합니다.

3. Two-way 접근: Consistency Models

   • 최근 제안된 Consistency Models는 “정확도(혹은 일관성) + 빠른 추론” 두 가지를 모두 달성하기 위한 방법으로 주목받고 있습니다.
   • Training free와 Training based 방식을 절충하거나,
     정확한 근사식을 통해 샘플링 단계를 줄이면서
     높은 품질을 유지하는 방법론 등이 연구되고 있습니다.

2.1 DDIM(Denoising Diffusion Implicit Models)

1. DDPM 복습: Markovian Forward Process

1.1 DDPM의 Forward Process 정의

DDPM에서는 데이터 $x_0$를 점진적으로 노이즈화(noise up)하는 다음의 Markov chain을 사용합니다.

이때 각 단계에서

• $\alpha_t$는 시간 스텝 $t$에서의 노이즈 스케줄링 파라미터로서, 일반적으로 $\alpha_t := 1 - \beta_t$ 형태로 정의합니다. ($\beta_t$는 매우 작은 양의 값)
• 위 식에서 볼 수 있듯이, $x_t$는 $x_{t-1}$만을 참고하여 정규 분포에서 샘플링되므로 Markov 가정이 성립합니다.

1.2 DDPM의 Marginal 분포

DDPM의 중요한 성질 중 하나는, 전체적인 forward process의 marginal인 $q(x_t \mid x_0)$가 간단히 다음과 같은 정규분포 형태로 표현된다는 점입니다.

2. DDIM: Non-Markovian Forward Process

2.1 아이디어: $\sigma$로 제어되는 Non-Markovian 확장

DDIM에서는 forward 과정을

1. Markov 가정 해제: $x_t$가 단순히 $x_{t-1}$에만 의존하지 않고, $x_0$와도 직접적으로 연결되도록 함
2. 잡음 크기($\sigma$) 도입: forward 과정의 임의성을 직접적으로 제어할 수 있도록 $\sigma_t$를 추가

하는 방식으로 확장합니다. 따라서 DDPM에서의

와 달리, DDIM은

라는 non-Markovian 분포를 정의합니다. 식으로 쓰면(개념적으로),

여기서 $\sigma_t^2$는 $t$ 시점에서의 잡음 세기를 나타내며, $\sigma \to 0$으로 만들 수도 있습니다.

2.2 $\sigma \to 0$에서의 Deterministic Forward & Sampling

• 만약 $\sigma_t^2$를 0에 가깝게 두면, 위의 분포가 Dirac delta에 가까워지며, 사실상 결정론적(deterministic) 과정이 됩니다.
• 이는 샘플링 단계에서 역전파(backward) 시에도 $x_t$와 $x_0$가 주어졌을 때 $x_{t-1}$이 유일하게 정해지는 형태가 됩니다.

2.3 DDIM의 샘플링 식

공식 자료에서는 DDIM의 (역) 샘플링 과정을 다음과 같이 요약합니다:

• 첫 항: 예측된 $x_0$에 $\sqrt{\alpha_{t-1}}$을 곱한 것
• 두 번째 항: $x_t$에 대한 “오차 방향”
• 세 번째 항: $\sigma_t$ 스케일의 새로운 랜덤 노이즈($\epsilon_t$)

중요:

• $\sigma_t = \sqrt{(1-\alpha_{t-1})/(1-\alpha_t)}\,\sqrt{1-\alpha_t/\alpha_{t-1}}$ 형태로 잡으면 Markovian 프로세스가 되고,
• $\sigma_t = 0$에 수렴시키면 결정론적 과정이 되며, DDIM의 핵심 장점인 “짧은 스텝으로도 고퀄리티의 샘플 생성”이 가능해집니다.

3. 정리 및 요약

1. DDPM

   • 순차적(Markov) 노이즈 주입으로 간단한 구조
   • $q(x_t \mid x_0)$가 깔끔한 정규분포 형태
   • 다만, 샘플링 시 많은 스텝이 필요

2. DDIM

   • non-Markovian 확장: $x_t$를 $x_{t-1}$와 $x_0$ 모두로부터 고려
   • 파라미터 $\sigma$를 통해 forward 과정의 임의성을 조절
   • $\sigma \to 0$시 결정론적 샘플링 가능 → 더 적은 스텝으로도 품질 높은 이미지를 생성 가능

결론적으로, DDIM은 DDPM의 forward 과정을 일반화함으로써, 샘플링 효율과 품질을 동시에 추구할 수 있는 기법입니다.

2.2 Progressive Distillation for Fast Sampling of Diffusion Models

1. Background

• 고품질 샘플을 얻기 위해서는 수백~수천 번의 모델 평가가 필요할 수 있습니다.
• 샘플링 스텝 수를 줄이려 하면, 예를 들어 DDIM 같은 방법은 샘플 품질이 떨어지는 문제가 있습니다.

2. Contributions

• Progressive distillation 기법을 통해, 많은 스텝을 사용하는 Teacher(교사) diffusion 모델을 절반 이하 스텝만으로 샘플링 가능한 Student(학생) diffusion 모델로 증류(distill)합니다.
• 적은 스텝에서도 안정적이고 높은 품질의 샘플을 얻을 수 있습니다.
• 완전한 progressive distillation 절차는 기존 모델 학습과 비교해 시간이 크게 추가되지 않으므로, 학습(Train)과 테스트(Test) 모두에서 효율적인 솔루션이 됩니다.

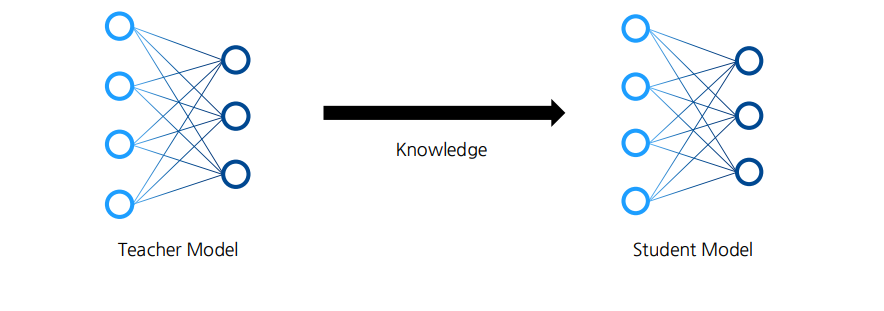
3. Knowledge Distillation

• 지식 증류(Knowledge distillation)란, 이미 학습된 거대 신경망(Teacher Network)이 가진 지식을 더 작고 가벼운 신경망(Student Network)에게 전수하는 방법입니다.
• 일반적으로 Teacher 모델의 출력(또는 중간표현)을 Student 모델이 모사하도록 학습하여, Student가 Teacher와 유사한 성능을 내도록 만듭니다.

4. Progressive Distillation

개념

• Progressive distillation은 Teacher diffusion 모델이 매우 느리고 스텝이 많은 대신 고품질을 만들어내는 점을 활용합니다.
• 먼저 Teacher 모델에서 작은 Student 모델로 증류를 수행하여 샘플링 스텝 수를 절반으로 줄입니다.
• 이후 Student 모델이 다시 Teacher 역할을 하여, 또다시 “절반 이하”로 줄인 스텝의 새로운 Student를 얻습니다.
• 이런 과정을 점진적으로 반복하면, 짧은 스텝에서도 Teacher 모델에 가까운 샘플 품질을 얻는 고속(High-speed) diffusion 모델을 얻을 수 있습니다.

프로세스 예시

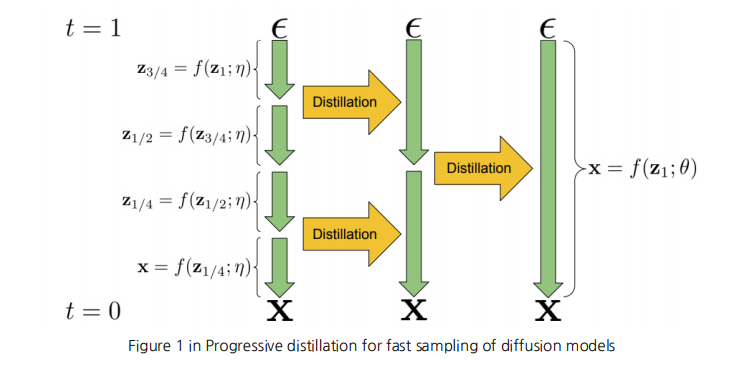
1. (t=1)에서 노이즈($\epsilon$)를 이용해 Teacher 모델이 생성 과정을 거칩니다:
   • $z_{3/4} = f(z_1; \eta)$
   • $z_{1/2} = f(z_{3/4}; \eta)$
   • $z_{1/4} = f(z_{1/2}; \eta)$
   • $x = f(z_{1/4}; \eta)$
2. 각 중간 스텝마다, Teacher가 만든 중간 결과물과 Distillation 작업을 수행해 Student가 모사하도록 학습합니다.
3. 최종적으로 t=0에서 Student 모델은 훨씬 적은 스텝으로 $x$에 근접한 샘플을 생성하도록 학습됩니다.

5. Diffusion Model Parameterization & Training Loss

표준 Diffusion 모델 학습 (Algorithm 1)

1. 데이터셋 $D$에서 $x \sim D$ 추출.
2. $t \sim U[0,1]$ (또는 일정한 스케줄)로 샘플링 후,
3. 노이즈 $\epsilon \sim \mathcal{N}(0, I)$를 추가해 $z_t = \alpha_t x + \sigma_t \epsilon$ 형태로 만들고,
4. 모델이 예측한 $\hat{x}$와 실제 깨끗한 데이터 $x$ 사이의 차이를 최소화하는 손실(예: MSE)을 계산합니다.
5. 반복하여 모델 파라미터를 업데이트합니다.

Progressive Distillation (Algorithm 2)

1. 이미 학습된 Teacher 모델 $\hat{x}_n(z_t)$가 있다고 가정합니다.
2. Student 모델도 동일한 방식으로 $z_t$를 샘플링하지만, Teacher로부터 DDIM 스텝을 통해 얻은 Teacher target $\hat{x}$를 이용해 Student의 출력을 학습합니다.
   • 즉, “원본 데이터 vs. 모델 출력” 간 차이를 최소화하는 대신,
   • “Teacher가 예측한 $\hat{x}$ vs. Student가 예측한 $\hat{x}_{student}$” 간의 차이를 최소화합니다.
3. 이러한 distillation 과정을 $K$번 반복할 때마다, Student 모델이 Teacher 성능에 가까워지면서도 샘플링 스텝은 절반으로 줄어듭니다.
4. 최종적으로 매우 소수의 스텝(예: 1~2스텝)만으로도 샘플 품질이 뛰어난 모델을 얻을 수 있습니다.

6. 결론

• Progressive distillation은 느리고 복잡한 Teacher diffusion 모델을 단계를 거쳐 빠르고 간단한 Student 모델로 만들 수 있는 효과적인 기법입니다.
• 적은 스텝에서도 고품질 샘플을 생성하며, Teacher 모델 대비 샘플링 시간이 크게 단축됩니다.
• 전체 distillation 과정을 반복할 때마다 학습 시간이 기하급수적으로 늘어나지 않으므로 실용적입니다.

2.3 Consistency Models

배경 (Background)

• 기존 확산 모델(Diffusion Model)의 샘플 생성 과정은 10~2000번의 반복 스텝이 필요합니다.

  • 이는 추론(Inference)에 오랜 시간이 걸려, 실시간(real-time) 애플리케이션에 적용하기가 까다롭습니다.

• Consistency Model은 확산 모델처럼 단계별 점진적 업데이트를 하지 않고도 한 번(혹은 소수의 스텝)만에 노이즈 상태에서 원본 이미지(데이터) 상태로 복원할 수 있도록 설계된 모델입니다.

기여 (Contributions)

1. 단 한 번의 스텝으로 어느 시점에서든 노이즈 상태($x_t$)를 원본 상태($x_0$)로 맵핑하는 모델을 제안합니다.
2. 소수 스텝(예: 1 스텝, 2 스텝 등) 생성에서도 기존의 여러 Diffusion Distillation 기법보다 더 우수한 성능을 보입니다.
3. 다른 생성 모델들 대비 짧은 추론 시간에도 뛰어난 성능을 보이며, Zero-shot 편집(Editing) 작업에도 사용될 수 있습니다.

확률적 미분방정식(SDE)와 Probability Flow ODE

1. Stochastic Differential Equation (SDE)(확률적 접근)

• 확산 모델에서 노이즈를 주입하는 과정을 수식화한 방정식입니다.
• 형태는 다음과 같습니다:
  $dx_t = \mu(x_t, t)\,dt + \sigma(t)\,dw_t$
  • $\mu(x_t, t)$: Drift 계수 $x_t$ 가 어떻게 평균적으로 움직이는지를 나타내는 항
  • $\sigma(t)$: Diffusion 계수 (시간에 따라 결정되는 노이즈(무작위) 스케일)
  • $w_t$: Brownian motion(위너 과정) 무작위 충격

---

🤔 Brownian motion이란 무엇인가?
Brownian motion(위너 과정)은 연속 시간에서 전개되는 확률적 과정**(Stochastic process) 중 하나로, 다음과 같은 특징을 가지고 있습니다:

1. $W_0 = 0$

   • 시간 $t=0$에서의 값은 0으로 정의됩니다.

2. 독립 증분(Independent increments)

   • 임의의 시점 구간들에서 발생하는 변화량(증분)이 서로 독립적입니다.

3. 정규 분포 증분(Normally distributed increments)

   • 시간 구간 $[s, t]$에 대한 Brownian motion의 증분 $W_t - W_s$는
     평균이 0, 분산이 $t-s$인 정규 분포를 따릅니다:
     $W_t - W_s \sim \mathcal{N}\bigl(0,\,(t-s)\bigr).$

4. 연속 경로(Continuous paths)

   • 시계열적으로 파동하는 궤적이 있으며, 이 경로들은 대부분 연속적입니다.

금융 분야에서는 이 Brownian motion(위너 과정)을 자산 가격의 무작위 변동 모델링(예: Black-Scholes 모델)에 활용합니다.
간단히 말해, Brownian motion은 무작위로 움직이는 입자(또는 자산 가격)의 궤적을 수학적으로 묘사하는 핵심적인 확률 모델입니다.

---

2. Probability Flow ODE(결정록적 접근)

• 위의 SDE를 확률적 과정과 동일한 마진 분포를 갖는 결정론적 ODE로 변환한 형태입니다.
• 다음과 같이 표현됩니다:
  $dx_t = \bigg[\mu(x_t, t) - \tfrac{1}{2}\sigma(t)^2 \nabla \log p_t(x_t)\bigg] dt$
• 이 식은 "SDE에서 브라우니안 모션을 제거한 형태"로 볼 수 있으며,
  ODE 해석만으로도 SDE와 동등한 결과(distribution)를 얻을 수 있게 해줍니다.
  즉,확률 과정(SDE)로 얻을 수 있는 분포”를, “무작위 없이(ODE 기반으로) 동일하게 복제”해주는 것이 PF ODE

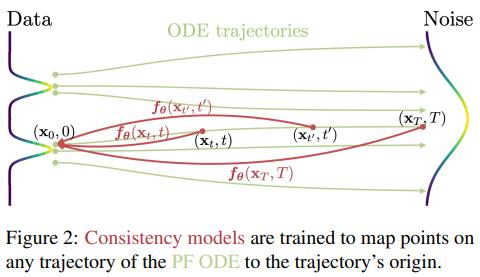
Consistency Model의 개념

$f_\theta$:

• PF ODE(Probability Flow ordinary differential equation)의 임의의 시점 ($x_t, t$)에 대해, 데이터의 시작점($x_0$)으로 한 번의 함숫값으로 매핑하는 네트워크입니다.

• Self-consistency라는 속성을 만족해야 합니다:

  • 동일한 PF ODE 궤적에 속하는 어떤 시점들 ($x_t, t$)과 ($x_{t'}, t'$)이 있으면,
    $f_\theta(x_t, t) \;=\; f_\theta(x_{t'}, t')$
    가 되어야 합니다.
  • 즉, 종단점(원본 데이터 $x_0$)으로 가는 결과가 일치해야 합니다.

Boundary Condition

• $f_\theta(x_t, 0) = x_0$ 이어야 합니다.
  • $t=0$일 때, 노이즈가 전혀 없는 원본 상태로 정확히 매핑됨을 의미합니다.
  • 이를 위해 네트워크 파라미터화 시 Skip Connection 구조를 사용합니다:
    $f_\theta(x_t, t) = c_\text{skip}(t)\,x + c_\text{out}(t)\,F_\theta(x_t, t)$
    • $c_\text{skip}(0) = 1$, $c_\text{out}(0) = 0$ 로 설정하면, $t=0$에서 $f_\theta(x_0, 0) = x_0$가 보장됩니다.

---

🤔$c_{skip}$과 $c_{out}$은 무엇인가?

$c_{skip}$와 $c_{out}$은 각각 “skip” 계수와 “output” 계수 정도로 볼 수 있습니다:

$c_{skip}(t)$:

말 그대로 skip connection에 해당하는 계수로, 원본 입력 x를 그대로 모델 출력에 반영할 때의 가중치 역할을 합니다.
t=0일 때 $c_{skip}(0)$=1이라면, 이 시점에서는 “모델의 다른 계산 부분을 전부 무시하고($c_{out}(0)$=0) 원본 데이터만 그대로 쓰겠다”는 의미가 됩니다.
$c_{out}(t)$:

모델의 메인 처리부(Fθ)에서 나오는 출력을 얼마나 반영할지를 결정하는 계수입니다.
t=0에서는 $c_{out}(0)$=0이므로 모델 출력을 사용하지 않고, t가 점차 증가하면 $c_{out}(t)$가 커져서 모델의 “학습된 변환”이 점차 많이 반영되는 구조가 됩니다.
즉, 둘은 시간 t가 변함에 따라 “원본 입력을 그대로 쓰는 정도($c_{skip}(t)$)”와 “네트워크 변환 출력을 반영하는 정도($c_{out}(t)$)”를 동적으로 조절하는 매개변수라고 보시면 됩니다.

---

Consistency Model의 학습 구조

1. Self-consistency 학습 (Distillation)

• Diffusion Distillation 기법을 차용하여, 미리 학습된 스코어 함수(혹은 확산 모델)에서 얻은 ODE 해(solution)를 단 한 번의 모델 추정으로 맞추도록 합니다.
• 구체적으로는:
  • 시간 $t'$에서의 상태 $x_{t'}$를 샘플링 후, ODE 솔버(Diffusion 모델의 score function 사용)를 통해 다른 시간 $t$로 가져간 샘플 $x_t^\phi$를 구합니다.
  • 이후 Consistency Model은 $f_\theta(x_{t'}, t')$와 $f_\theta(x_t, t)$가 서로 같아지도록(= 같은 $x_0$를 복원) MSE로 학습합니다:
    $\min_\theta \big\lVert f_\theta(x_{t'}, t') \;-\; f_\theta(x_t, t)\big\rVert_2^2$

2. Isolation Training

• 스코어 모델을 사전에 학습하지 않고도 Consistency Model 자체를 바로 학습하는 방법입니다.
• 편의상, $x + t_{n+1} z$ 같은 형태로 SDE/ODE의 노이즈 추가를 흉내내어 모델을 업데이트합니다.
  $\min_\theta \,\lambda(t_n)\big\lVert f_\theta \big(x + t_{n+1} z,\, t_{n+1}\big)\;-\;\text{stopgrad}\big(f_\theta(x + t_n z,\, t_n)\big)\big\rVert_2^2$
• 실제 확산 모델의 스코어 함수 대신, 무편향 추정값으로 한 번에 복원하는 Consistency Model을 직접 학습시킵니다.
  

결론

• Consistency Model은 기존 Diffusion 방식의 장시간 추론 문제를 해결하기 위해 고안되었습니다.
• 이 모델은 어느 시점의 노이즈 상태에서든 한 번의 네트워크 평가로 원본 데이터에 가까운 결과를 복원합니다.
• Self-consistency, Boundary Condition 등을 만족하기 위해 Distillation 또는 Isolation 방식으로 학습할 수 있습니다.
• 결과적으로 추론 시간이 매우 짧아 (단 1~2 스텝) 실시간 응용이 가능하며, 생성 품질도 우수하여 이미지 생성 및 편집 같은 여러 작업에 활용도가 높습니다.

3. Conditional Image Generation

조건은 다양한 형태로 줄 수 있다 ex) 정보, 문맥, 속성 등등

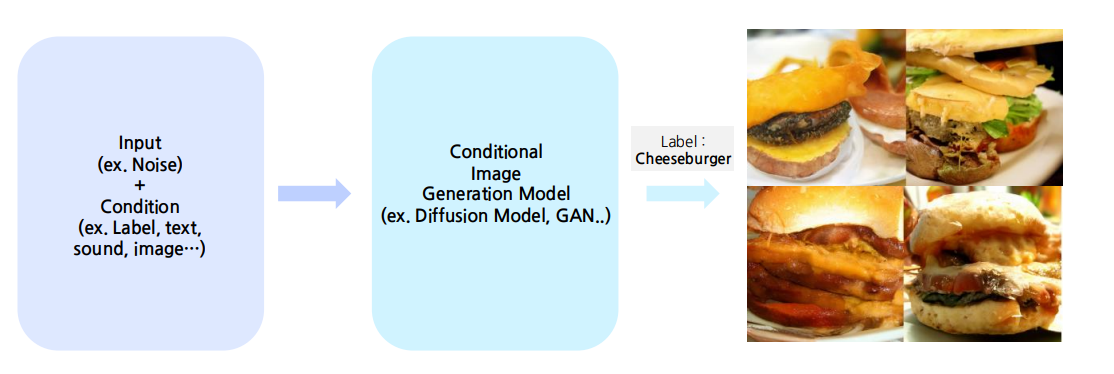
Why Conditional Generation is necessary?

We can control the model’s power through this.

• We can provide the desired conditions to the model and instruct it to generate the desired output.
• Conditions in conditional image generation can take various forms, including images, sounds, text, or any other suitable input types.

Through this, We can generate what we want
우리가 원하는 형태로 이미지가 생성가능하기 때문에 Conditional Generation이 중요하다.

3.1 Diffusion Models Beat GANs on Image Synthesis

Classifier Guidance로 살펴보는 조건부 확률 생성의 원리

1. 배경

• Diffusion 모델은 원래 이미지 생성을 ‘무(無)’에서 시작해 점차 이미지를 그려가는 방식(확률적 과정)으로, “무조건부(unconditional) 생성”에서 뛰어난 성능을 보여왔습니다.
• 하지만 우리가 원하는 특정 클래스(예: 고양이, 자동차 등)를 조건으로 달아 이미지를 생성하고 싶을 때에는, 기존 방법만으로는 어려움이 있습니다.

2. Classifier Guidance란?

• “Classifier Guidance”는 추가로 학습된 분류기(classifier)의 기울기(gradient)를 활용해, Diffusion 모델이 이미지를 생성할 때 원하는 클래스 방향으로 가도록 유도(guidance) 해주는 방법입니다.
• 즉, Diffusion 모델이 이미지를 그려가는 각 단계에서,
  “이 클래스일 확률이 높아지는 쪽”으로 한 번 더 가중을 줌으로써
  원하는 레이블의 이미지를 더 잘 생성하도록 만들어준다고 볼 수 있습니다.

3. Classifier Guidance가 들어간 샘플링 과정 (간단 버전)

Algorithm 1 (Classifier Guided Diffusion Sampling)

1. 초기값 $x_T$를 $\mathcal{N}(0, I)$ 에서 샘플링합니다.
2. 매 시점 $t$부터 1까지 다음을 반복합니다.:
   • Diffusion 모델에서 평균, 분산 $(\mu_\theta(x_t), \Sigma_\theta(x_t))$를 구합니다.
   • 그다음, 분류기 $p_\phi(y|x_t)$ 의 로그 확률의 기울기 $\nabla_{x_t} \log p_\phi(y|x_t)$를 계산해 샘플링 시 평균값에 추가로 더해줍니다.
   • 즉, 기존에는 $x_{t-1}$ 을 그냥 $\mathcal{N}(\mu, \Sigma)$ 에서 뽑았다면,
     이제는 $\mu + s \Sigma \nabla_{x_t} \log p_\phi(y|x_t)$ 처럼
     클래스 방향으로 살짝 당겨진 분포에서 뽑게 됩니다.
3. 최종적으로 $x_0$을 얻으면, 조건부로 생성된 이미지가 완성됩니다.

Algorithm 2 (Classifier Guided DDIM Sampling)

위 과정은 DDIM(Denoising Diffusion Implicit Models) 샘플러 버전에도 똑같이 적용할 수 있습니다.단순화해서 말하자면, DDIM에서 쓰이는 ‘예측 노이즈’ $\epsilon_\theta(x_t)$ 부분에다가 분류기의 기울기 항을 추가하여, 조건(class label) 방향으로 조금 더 이동시켜 주는 방식입니다.

4. 왜 이 방법이 좋을까?

조건을 달아도 품질이 크게 떨어지지 않으면서 내가 원하는 클래스의 이미지를 잘 뽑을 수 있습니다.GAN 기반의 조건부 생성과 비슷한 성능을 내면서도 Diffusion 특유의 안정적이고 다양한 이미지를 뽑는 장점을 살릴 수 있습니다.

Tip:

$s$ (gradient scale)을 조절해가며얼마나 ‘클래스 방향’을 강하게 반영할지 정할 수 있습니다.
$s$가 너무 크면 이미지가 해당 클래스에 과도하게 수렴해버릴 수 있고
너무 작으면 조건의 효과가 미미할 수 있으니, 적절한 값을 찾는 것이 중요합니다.

3.2 Classifier-Free Diffusion Guidance

“별도의 분류기(classifier)를 학습하지 않고도 조건부 생성을 가능하게 해주는 방법!”

1. 배경

• Classifier-Guidance에서는 별도의 분류기가 필요했습니다.
  • Diffusion 모델에 추가 학습된 분류기의 기울기를 더해서 이미지를 생성했었습니다..
• 하지만, 분류기를 따로 학습하려면 시간과 리소스가 더 들고, 실제 활용할 때도 분류기 모델이 추가로 필요하게 됩니다.

2. Classifier-Free Guidance 아이디어

• Diffusion 모델 하나만 가지고도 조건(condition)을 줄 수 있게 만들자는 아이디어!
• 어떻게?
  1. 조건(레이블, 텍스트 등) 없이도 이미지를 잘 생성하도록(Unconditional),
  2. 조건이 있을 때도 이미지를 잘 생성하도록 (Conditional),
     두 가지를 동시에 학습해버리는 겁니다..!
• 즉, 모델에게 가끔씩 조건을 빼고(=빈칸 처리) 학습시키면,
  조건이 있는 경우와 없는 경우를 한 번에 배우는 셈이 됩니다.

3. Training (Algorithm 1)

확률 $p_{uncond}$만큼, 조건 c를 지워버린 상태로 학습을 하므로,모델 $ϵ_θ$는
“조건이 있을 때”의 노이즈 예측,“조건이 없을 때”의 노이즈 예측 둘 다 배우게 됩니다.

4. Sampling (Algorithm 2)

실제 샘플링(이미지 생성) 단계는 기존 Diffusion과 비슷하지만,
‘조건이 있을 때의 예측(Conditional)’과 ‘조건이 없을 때의 예측(Unconditional)’를 적절히 섞어서 분류기 없이 클래스(또는 텍스트) 방향으로 유도합니다.

핵심 공식

$ϵ_θ(z_t, c)$ : “조건이 있을 때” 예측
$ϵ_θ(z_t)$ : “조건이 없을 때” 예측
$w$ : 조건을 얼마나 강하게 반영할지 결정

4. Text-to-Image Synthesis

text input 을 넣어서 text 와 correspond한 image를 만드는 것입니다.

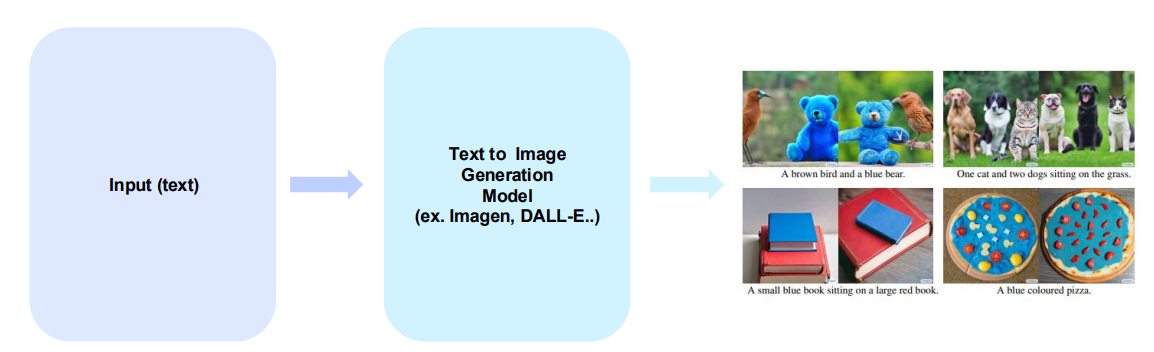
Why text-to-image is necessary?

text를 통해서 우리는 좀 더 detail한 생각을 전달할 수 있습니다.

• 데이터에 대한 패턴, 특징, 통계적 특성을 identifying 및 modeling 할 수 있게 합니다.

4.1 Photorealistic Text-to-Image Diffusion Models with Deep Language Understanding

• 핵심 아이디어

  • 기존 연구들과 달리, 단순히 이미지-텍스트 쌍만 활용하는 것이 아니라, 텍스트 전용 대규모 언어 모델(LLM)의 사전학습된 임베딩을 활용해 더 깊은 언어 이해를 달성함.
    (one of the key findings in Imagen is the effectiveness of pre-trained text embeddings from large language models trained exclusively on text corpora in text-to-image synthesis)
  • 대규모 언어 모델(예: T5-XXL)에서 추출한 텍스트 임베딩이, 이미지 생성 품질과 이미지-텍스트 일치도를 높이는 데 매우 효과적임을 발견함.

• 구조 (Imagen 예시)

  1. 고정된 T5-XXL 인코더
     • 입력 텍스트를 임베딩 시퀀스로 변환.
  2. 2개의 초해상도(슈퍼-해상도) 확산 모델
     • 하나는 256×256 이미지를 생성하고, 다른 하나는 1024×1024 이미지를 생성.
  3. 클래스 파이어 없이(=Classifier-Free) 가이던스 기법 적용
     • 텍스트 임베딩을 조건으로 하여, 샘플링 과정에서 가이던스 강도를 크게 높일 수 있는 새로운 샘플링 기법을 도입.
     • 결과적으로 이전 연구 대비 더 높은 이미지 품질(Fidelity)과 더 정확한 이미지-텍스트 정합(Alignment)을 달성.

4.2 Hierarchical Text-Conditional Image Generation with CLIP latents

배경 (Background)

• 이미지-텍스트 쌍을 활용해 텍스트-이미지 모델을 구축하는 데 있어, CLIP 등 대조학습(Contrastive) 기반 모델이 매우 효과적입니다.

• CLIP은 텍스트와 이미지를 동일한 임베딩 공간에 매핑하면서도, 이미지의 의미를 견고하게 학습하기로 유명합니다.

• 기여 (Contributions)

  • CLIP 임베딩을 활용하면, 텍스트-이미지 생성 모델 트레이닝에 큰 이점이 있음을 확인.
  • 텍스트에서 만든 임베딩을 조건(condition)으로 받아, 확산 모델(diffusion model)을 통해 이미지를 생성하는 2-단계 모델을 제안.
    1. 단계 1 (Stage 1): Prior 네트워크
       • 텍스트를 입력으로 받아, 해당 텍스트에 대응하는 이미지 임베딩을 생성.
    2. 단계 2 (Stage 2): Diffusion 모델
       • 앞서 생성된 이미지 임베딩을 조건으로 삼아 이미지를 생성.

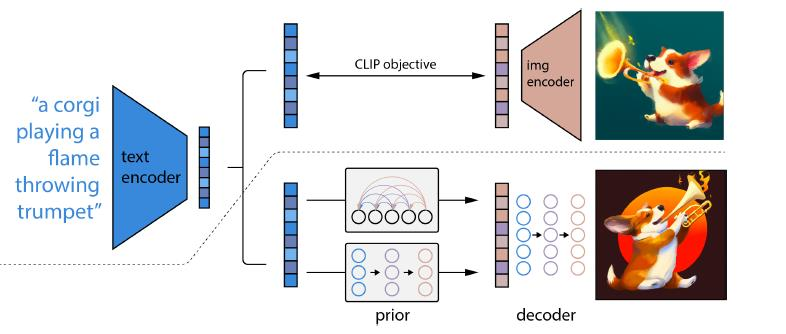
• 장점 및 특징
  • 제안된 방식은 텍스트와 유사도가 높은, 시각적으로 그럴듯한 이미지를 생성 가능.
  • 입력 이미지가 주어졌을 때, 이미지 의미를 유지하면서도 다양한 변형 이미지를 만들어낼 수 있음.

5. Image-to-Image Translation

Image-to-Image translation generally encompasses various tasks, including style transfer, colorization, transformations between specific domains, and more.

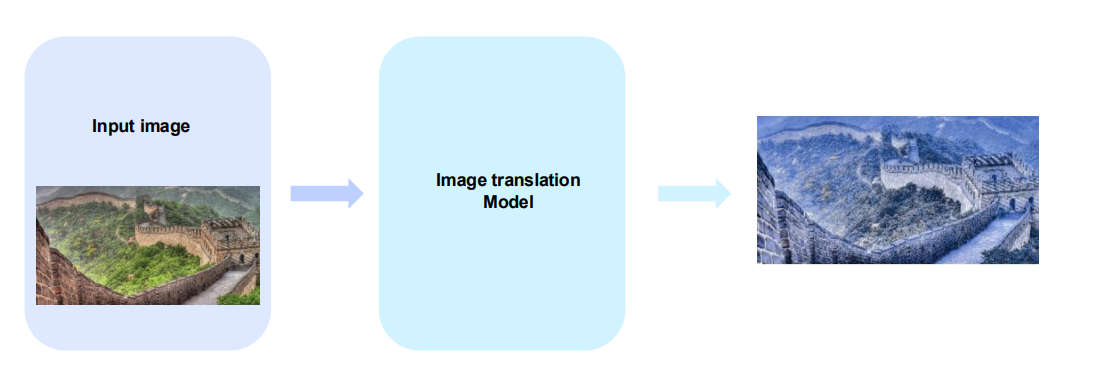
Why Image translation is necessary?

• Imgae-to-Image 를 통해, 우리가 원하는 이미지를 얻을 수 있습니다.
• Imgae-to-Image 를 통해, 우리가 원하는 도메인 이미지로 변형할 수 있습니다.
• Imgae-to-Image 를 통해, visual적으로 향상시킬 수 있습니다.

5.1 SDEdit: Guided Image Synthesis and Editing with Stochastic Differential Equations

배경 (Background)

• 최근 확산 모델(Diffusion Models)을 확률 미분방정식(SDE) 형태로 해석하는 이론이 발전하면서, 이를 이미지 조작(Image Manipulation)에도 활용하려는 시도가 증가.

• 기여 (Contributions)

  • SDEdit: 가이드 이미지를 주고, SDE 기반의 Forward-Backward(역추론) 과정을 통해 원하는 이미지를 자연스럽게 복원하거나 편집할 수 있는 기법 제시.
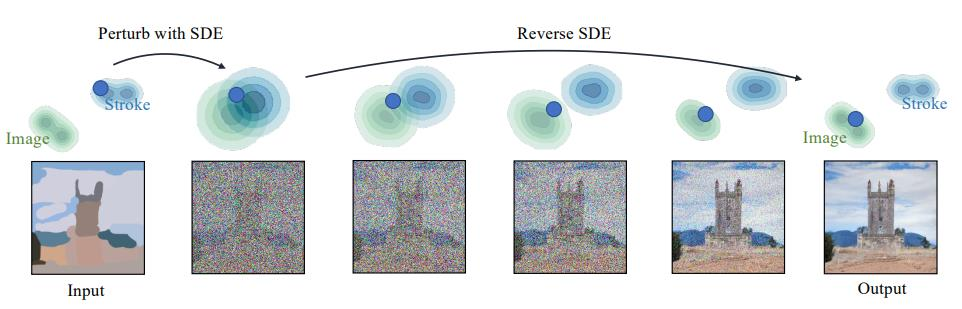
  • 이미지의 윤곽이나 색상 블록(Stroke)만 간단히 주어도, 확산 모델을 통해 시각적으로 일관성 있고 자연스러운 최종 이미지를 얻음.

• 핵심 아이디어

  1. Forward 과정
     • 가이드 이미지를 SDE를 통해 점차 노이즈화(또는 섞음).
  2. Reverse 과정
     • 확산 모델이 이 노이즈화된 상태를 다시 복원(역추론)해가면서, 가이드 정보를 반영한 최종 이미지를 생성.
  • 이 과정을 통해, 이미지 편집, 스타일 변환, 형태 보정 등 다양한 이미지 조작 기능을 수행 가능.

5.2 DDIB: Dual Diffusion Implicit Bridges for Image-to-Image Translation

• 배경 (Background)

  • 기존에 확산 모델(Diffusion Models)을 활용한 이미지 변환(Image Translation) 연구는 상대적으로 덜 활발히 진행되어 왔음.
  • 이를 보완하기 위해, 이미지 변환에 확산 모델을 적용한 연구를 시도.

• 기여 (Contributions)

  1. Schrödinger's Bridge를 활용하여, 한 도메인의 이미지를 다른 도메인으로 변환하는 이미지 번역을 시도.
  2. DDIB (Diffusion-based Domain-Interchange Bridge) 기법 제안:
     • 두 개의 확산 모델을 통해 한 도메인의 이미지를 다른 도메인 이미지로 바꾸는 과정을 단일 모델 구조 내에서 수행.

• 모델 개요

  1. 1단계: 한 도메인에 대해 확산 모델을 학습하고, 이를 ODE Solver를 사용해 잠재 표현(latent representation)으로 변환.
  2. 2단계: 변환된 잠재 표현을 다시 ODE Sampling하여, 목표 도메인의 이미지로 이미지 변환을 수행.
  • 전체적으로, 두 번의 ODE 기반 추론(Forward & Reverse)을 통해 도메인 간 이미지 변환을 달성함.

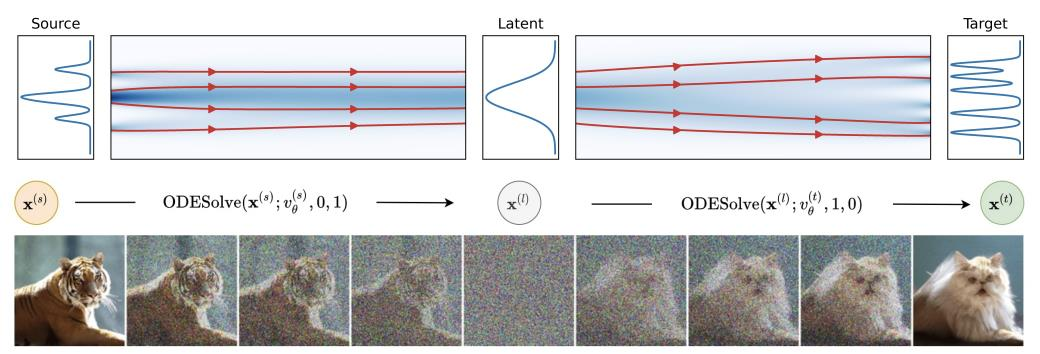
The algorithm below provides a concise representation of the process in DDIB:

5.3 Adding Conditional Control to Text-to-Image Diffusion Models

• 배경 (Background)

  • 대규모 모델(예: 대형 확산 모델)은 이미 학습되어 있는 무거운 파라미터를 다시 학습하기에는 비용이 큼.
  • 원래 모델이 학습된 특정 조건 이외의 새로운 조건을 추가하려면, 모델 전체를 재학습해야 했던 단점이 존재.
    

• 기여 (Contributions)

  1. ControlNet 모듈 제안
     • 원래 모델의 가중치(locked 상태)를 그대로 두면서, 새로운 조건 정보(예: depth, Canny edge, segmentation map)를 받아들여 이미지를 생성할 수 있도록 함.
  2. Zero-Convolution(1×1 conv, weight & bias를 0으로 초기화)를 사용
     • 기존 모델의 파라미터를 건드리지 않고도, 새로운 조건에 대해 학습할 수 있도록 지원.
  3. 학습 비용 절감
     • 처음부터 모델 전체를 재학습할 필요 없이, ControlNet 부분만 추가 학습하면 되므로 비용과 시간이 크게 절감됨.

• 핵심 아이디어

  • Locked 파라미터: 원래 Diffusion 모델의 가중치는 변경되지 않음.
  • Trainable Copy & Zero Convolution: ControlNet 내부에서만 학습 가능한 가중치를 두어, 새로운 조건을 반영하고, 원래 모델의 성능은 해치지 않음.
  • 이를 통해 다양한 가이드 신호(깊이 정보, 엣지 맵, 분할 맵 등)를 이미지 생성 과정에 반영 가능.

  

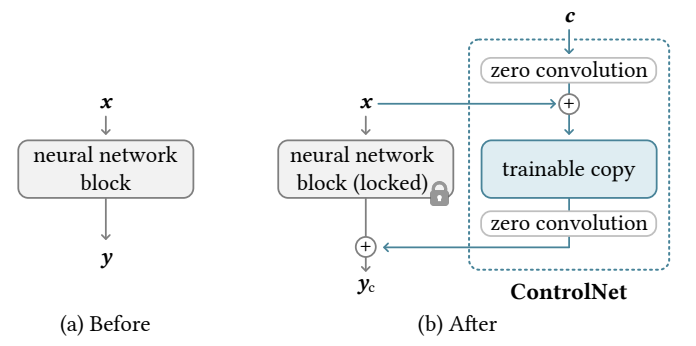
위 그림은 원래 모델(왼쪽, Before)과, ControlNet을 추가한 이후의 모델(오른쪽, After) 구조를 비교한 것입니다.
핵심 아이디어는 기존 신경망 블록(이미 학습된 모델의 가중치)을 잠그고(locked), 새로운 ControlNet 모듈을 덧붙여서 추가적인 조건(예: depth, Canny edge, segmentation map 등)을 받아들일 수 있게 만드는 데 있습니다.

1. Before (왼쪽 그림)

• Neural Network Block
  • 사전에 학습된 확산 모델(또는 U-Net의 일부 등)이 하나의 블록으로 표현됨.
  • 입력 $\mathbf{x}$를 받아 출력 $\mathbf{y}$를 생성.
  • 과거에는 새로운 조건(예: 추가적인 가이드 맵)을 적용하려면, 이 블록의 가중치를 다시 학습해야 했음.

2. After (오른쪽 그림)

• Neural Network Block (Locked)

  • 기존 모델의 가중치를 변경 없이 고정(freeze)시킨 채로 사용.
  • $\mathbf{x}$를 입력받고, 그 출력 $\mathbf{y}$에 해당하는 정보를 하단으로 내보냄($\mathbf{y_c}$).

• ControlNet 모듈

  • 새로운 조건 $\mathbf{c}$(예: depth 맵, edge 맵)를 입력으로 받아,
  • 기존 모델의 출력을 보조/조정해주는 추가적인 학습 가능한 복제본(trainable copy) 블록을 포함함.
    • 여기서 trainable copy란, 원래 블록과 유사한 구조(혹은 임의의 구조)를 가지되,
      학습 가능한 파라미터를 새로 둔 모듈을 의미함. (원래 블록은 고정되어 있기 때문에 영향 없음)
  • Zero Convolution(0으로 초기화된 가중치와 바이어스를 갖는 1×1 컨볼루션)을 이용
    • 학습 초기에는 조건 $\mathbf{c}$가 모델 출력에 영향을 주지 않는 상태에서 시작.
    • 모델이 학습을 진행하면서, 점차 $\mathbf{c}$를 활용해 원하는 형태의 정보를 반영할 수 있게 됨.

• 결과

  • 원래 모델의 가중치를 건드리지 않고, ControlNet만 추가로 학습하면,
  • 원하는 새 조건(깊이, 엣지, 분할 맵 등)을 반영한 이미지 생성이 가능해짐.
  • 학습 비용이 적게 들고, 기존 모델의 성능을 해치지 않으면서도, 확장성이 크게 향상됨.

정리

• (a) Before: 사전학습된 모델만 있음. 새로운 조건을 적용하려면 모델 전체를 재학습해야 함.
• (b) After: ControlNet을 도입.
  • 기존 모델 블록은 locked 상태 유지.
  • 새 블록(trainable copy)과 Zero Convolution을 통해, 새로운 조건$\mathbf{c}$를 손쉽게 반영.
  • 결과적으로, 효율적인 Fine-tuning으로 다양한 조건을 처리할 수 있는 구조 달성.

6. Image Customization

The primary goal of image customization is to freely transform an image into the desired form.즉, 내가 원하는 형태로 변형시키기.

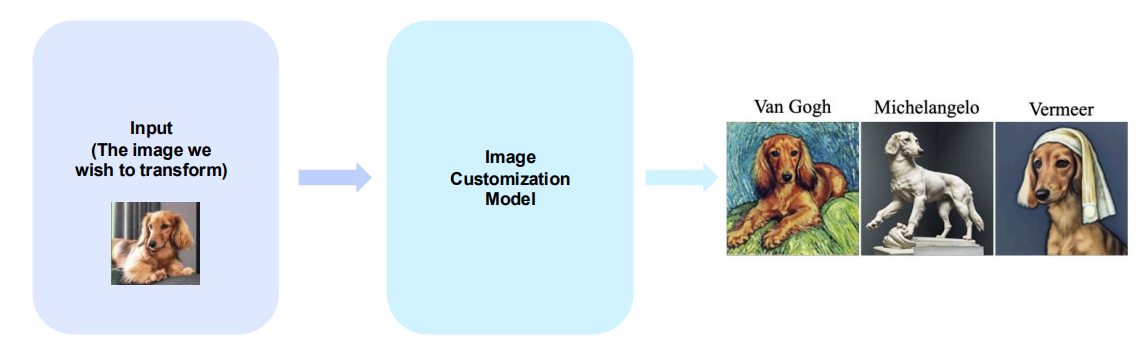
Why Image Customization is necessary?

• Creativity and Artistry
  예술가와 디자이너가 이미지 커스터마이징을 통해 다양한 스타일, 미적 효과, 예술적 표현을 실현할 수 있음.

• Personalization
  이미지 커스터마이징은 개인화 경험을 제공함. 예를 들어, 사용자에게 맞춤형 이미지를 제공하면 제품이나 서비스에 대한 인상을 더욱 높일 수 있음.

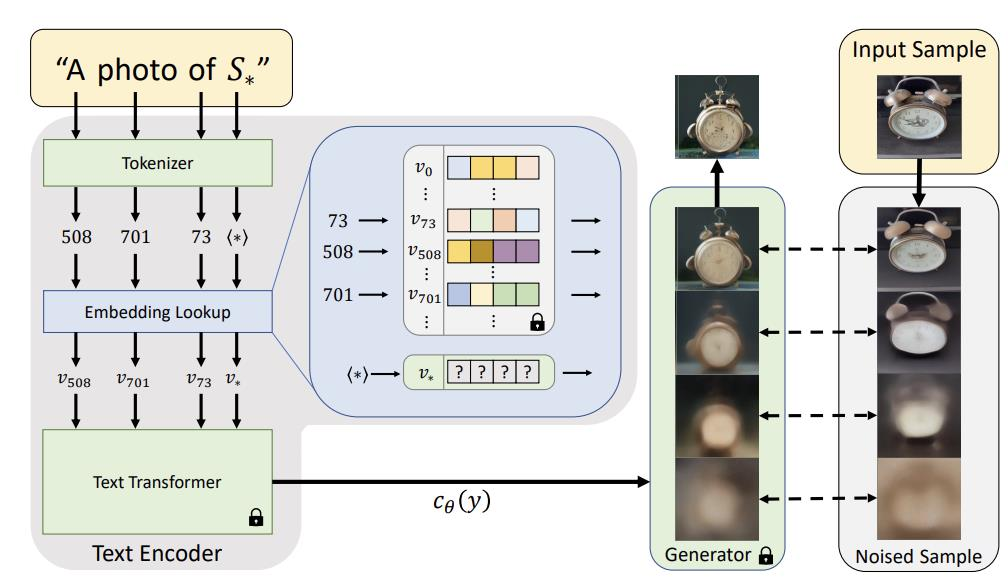
6.1 An Image is Worth One Word: Personalizing Text-to-Image Generation using Textual Inversion

• 배경 (Background)

  • 텍스트-이미지 모델의 발전으로, 텍스트 설명만으로 원하는 이미지를 맞춤화하고자 하는 요구가 증가.
  • 예전에는 이미지→텍스트 매핑이 아닌, 주로 텍스트→이미지 생성을 다룬 연구가 중심이었음.

• 기여 (Contributions)

  1. 이미지를 텍스트로 임베딩(inversion)하는 방식을 처음 시도.
  2. 이렇게 임베딩된 이미지를 다시 텍스트 설명을 통해 자유롭게 변형(커스터마이징)할 수 있는 방법을 제시.

• 핵심 아이디어

  • 원하는 이미지를 “$S^*$”라는 토큰(placeholder)으로 치환한 뒤,
    • 예: “A photo of $S^*$” 같은 문장을 여러 개 준비해 모델을 학습.
  • 그 결과, 모델은 이미지의 개념을 $S^*$ 토큰에 내재화(inversion)하게 됨.
  • 이후, “An oil painting of $S^*$” 등 다른 텍스트를 주면,
    • $S^*$ 토큰이 포함된 문맥에 맞춰, 원본 이미지를 원하는 스타일로 자유롭게 변환.

• 전체적인 작업 흐름

  1. 학습:
     • 특정 이미지를 $S^*$로 표현한 여러 문장을 만들어, 확산 모델에 학습시킴.
  2. 커스터마이징:
     • 학습 후, “$S^*$”를 포함하는 다양한 텍스트 프롬프트로 이미지를 생성/편집.
     • 원본 이미지의 주요 컨셉은 유지하면서도, 텍스트에 따라 새로운 표현이 가능.

6.2 Dreambooth : Fine Tuning Text-to-Image Diffusion Models for Subject-Driven Generation

• 배경 (Background)

  • 기존의 텍스트 인버전(Textual Inversion) 기법은 특정 이미지를 텍스트 토큰으로 학습시키는 방식이지만,주변 텍스트나 클래스 정보가 망각(forgetting)되는 문제가 발생할 수 있음.

• 기여 (Contributions)

  1. Diffusion 모델에 이미지를 텍스트로 임베딩시키는 작업을 진행,
     • 이후 맞춤형 텍스트 설명을 통해 이미지를 자유롭게 생성 및 변형.
  2. DreamBooth:
     • 몇 장의 특정 주제(예: 한 마리의 개) 사진을 활용하여, 사전학습된 텍스트-이미지 모델을 미세조정(fine-tuning).
     • 결과적으로, 해당 주제를 다양한 문맥(해변, 무지개 카펫, 등)에 자연스럽게 배치 가능.

• 핵심 아이디어
  • Textual Inversion과 달리, DreamBooth는 “A [v] dog” (특정 개 이미지)와 “A dog” (개라는 클래스명)
    두 종류의 이미지를 동시에 학습해,
  • 모델이 기존에 알고 있던 “개”라는 클래스 정보를 유지하면서도,
    특정 개(주어진 사진)만의 고유한 특징을 새로운 맥락에 맞춰 생성할 수 있도록 함.

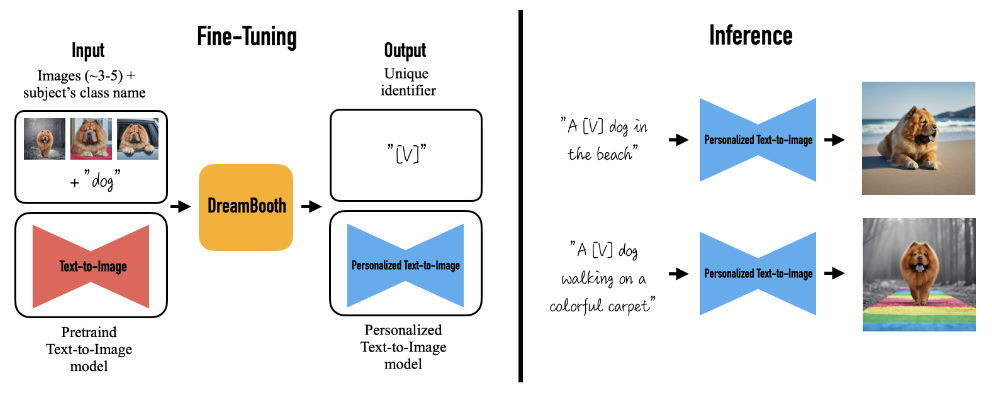
DreamBooth 개념과 구조 자세히 살펴보기

DreamBooth는 기존의 대형 Text-to-Image 모델(예: Stable Diffusion)을 특정 이미지(주제/개체)의 특징에 맞춰 개인화하는 기법입니다.
주로 3~5장 정도의 사진과 해당 주제의 클래스 이름(예: “dog”, “cat” 등)을 활용해서,
새로운 토큰(고유 식별자)을 모델 내부에 학습시킨 뒤,
“원하는 상황 속에서 그 주제(개체)를 자유롭게 표현”하는 이미지 생성이 가능하게 만듭니다.

1. 전체 흐름 요약

1. Fine-Tuning 단계

   • 입력:
     • 3~5장의 이미지 (예: 특정 강아지 사진)
     • 대상(주제)의 클래스 이름 (예: “dog”)
   • 핵심 아이디어:
     • 모델이 주제(예: 특정 강아지)의 시각적 특징을 새로운 토큰(예: “[V]”)으로 학습합니다.
     • 즉, “[V] dog”라고 했을 때, ‘이 강아지’를 나타내는 토큰으로 인식하도록 하는 것이 목표입니다.
   • 결과: Fine-Tuning된 개인화된 Text-to-Image 모델
     • 이 모델은 “[V] dog”라는 텍스트를 입력받으면, 학습했던 특정 강아지의 형태를 잘 재현합니다.

2. Inference 단계

   • 예시:
     • “A [V] dog in the beach”
       • => 학습된 “[V]” 토큰 + “dog” + “in the beach” 문맥을 조합해
         해당 강아지를 해변에 있는 모습으로 그려냅니다.
     • “A [V] dog walking on a colorful carpet”
       • => 같은 강아지(= [V])가 화려한 카펫 위에서 걷는 모습을 생성
   • 효과:
     • 단 몇 장의 예시 사진만으로도,
     • 원하는 상황/배경 안에 특정 개체(주제)를 자유롭게 배치할 수 있게 됩니다.

2. 첫째 그림(Fine-Tuning 과정) 상세

(1) 입력

• 약 3~5장의 이미지 + 주제의 클래스 이름(“dog”)을 준비합니다.
• 이를 이미 학습된(Pretrained) Text-to-Image 모델에 넣고 DreamBooth로 Fine-Tuning합니다.

(2) Unique identifier 토큰 “[V]”

• Fine-Tuning 과정에서 “[V]”라는 새로운 토큰이 생성됩니다.
• 이 토큰은 해당 개(체)의 고유 특징(모양, 색깔, 구조 등)을 담기 위해
  모델 내부의 가중치가 업데이트됩니다.

(3) Fine-Tuned(개인화된) 모델 완성

• 학습이 끝나면, “[V] dog”라는 문구를 입력했을 때,
  기존에 보지 못한(새로운) 장면이나 포즈에서도
  ‘같은 강아지’를 생성할 수 있게 됩니다.

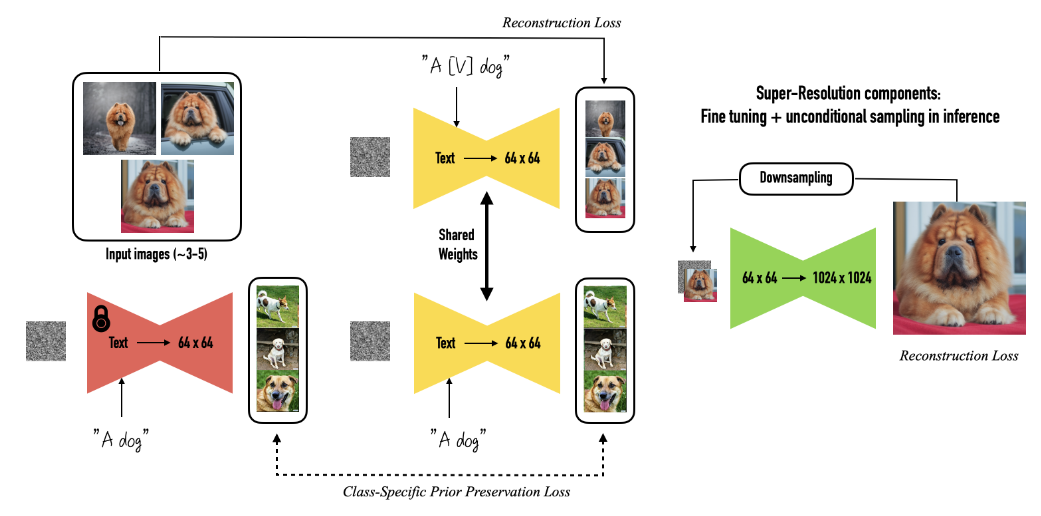
3. 오른쪽 그림(Inference와 내부 구조) 상세

1. Class-Specific Prior Preservation Loss

   • 모델이 “[V] dog”를 학습하는 과정에서
   • “dog” 전체 개념도 잊어버리지 않도록 별도의 Loss(=Prior Preservation)를 줍니다.
   • 예: “[V] dog” 이미지와 “a dog” 이미지 간 유사도를 적절히 유지
   • 이를 통해, 모델이 특정 개체만 알고 ‘개(dog)’라는 일반 클래스는 망각하지 않도록 학습합니다.

2. Shared Weights

   • Text-to-Image 모델은 텍스트 정보를 받아 이미지(64x64, 등)를 생성하는 오토인코더(또는 U-Net) 구조를 갖습니다.
   • Fine-Tuning 시, 기존 모델 가중치를 일부 혹은 전부 업데이트해서,
     “[V] dog”라는 텍스트 입력에 대해 새로운 시각적 표현을 학습합니다.

3. Super-Resolution

   • 64x64 크기의 중간 이미지를 1024x1024 등 고해상도로 키우는 후처리(업샘플링) 단계가 있습니다.
   • Fine-Tuning된 모델을 그대로 쓰거나, 추가적으로 업샘플러를 미세 조정(Fine-Tuning)하여
     고해상도 결과물을 얻습니다.
   • 이때도 Reconstrunction Loss 등을 적용해 이미지 품질을 유지합니다.

4. 왜 유용한가?

1. 적은 수의 이미지로도 특정 대상(개체)를 모델에 빠르게 주입할 수 있습니다.
2. 추가 토큰(예: “[V]”)을 이용해, 원래 모델이 알지 못했던
   새로운 개념(사람/동물/물건 등)도 생성할 수 있습니다.
3. 기존 “dog”와 같은 클래스 정보와 결합해,
   주제에 대한 일반적 특징도 유지하면서 특정 개체 특징을 반영할 수 있습니다.
4. 결과적으로, 보다 개인화된 이미지 생성이 가능해집니다.

##ㅍ# 5. 정리

• DreamBooth는 Pretrained Text-to-Image 모델을 약간의 이미지로 Fine-Tuning해서,
  나만의 토큰(예: “[V]”)을 모델에 학습시키는 기법입니다.
• 이를 통해, 단어 조합만으로 구체적이고 개성 넘치는 이미지를 만들 수 있습니다.
• Prior Preservation Loss 등을 활용해, 원래 클래스 전체의 특성도 함께 유지하도록
  모델이 Overfit되지 않도록 설계했습니다.

• 장점
  • 클래스 정보 보존: 원래 모델이 가지고 있던 일반적인 개에 대한 지식이 보존됨.
  • 고유한 주제의 재활용: 몇 장의 사진으로부터 독특한 개체(예: 한 마리의 개)를 학습해,
    텍스트 프롬프트로 다양한 장면이나 스타일로 개체를 재현 가능.
  • 결과적으로, 높은 충실도(Fidelity)로 특정 대상을 원하는 컨텍스트에 생성할 수 있음.

7. Erasing Concept

Erasing concept is a recent topic in large-scale models, where specific concepts are removed or erased from the model's understanding or representation.

The primary goal of erasing concept is to remove the concept we desire without affecting other concepts.

Why erasing concept is necessary?

• 최근 large model 이 무차별적으로 학습하므로, 해로운 content를 도출해냅니다.
• 하지만 다시 학습시키는 것은 너무나 많은 resource 가 듦
• 따라서 목적은 harmful 한 content를 제외하고 모델의 성능은 유지하는 것입니다.

7.1 Erasing Concepts from Diffusion Models

이 기법은 특정 컨셉(예: “Van Gogh” 스타일)을 모델에서 제거하고자 할 때 활용됩니다.
기존(동결된) 모델과 새로 학습할 모델의 출력 차이를 이용하여, 제거 대상 컨셉과 관련된 표현이 없어지도록 유도합니다.

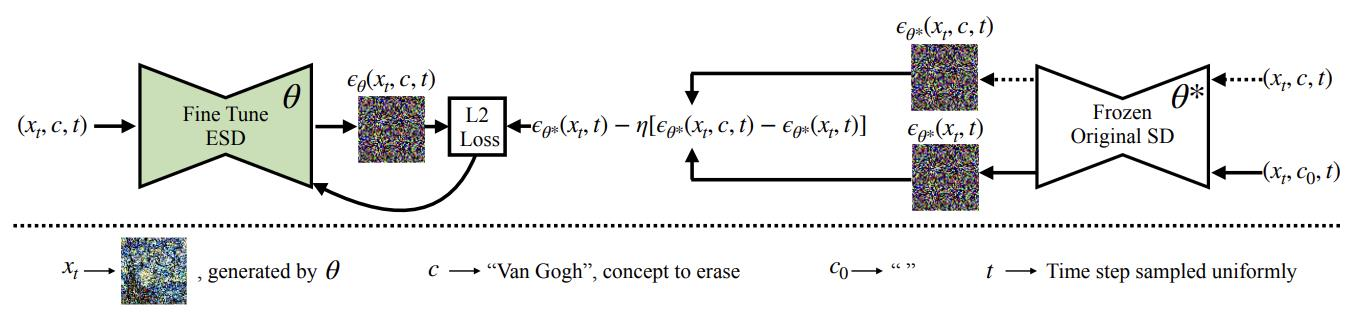
1. 제거하고 싶은 컨셉에 대한 이미지 생성

1. 동결된 모델($\theta^*$)에서 “제거 대상 컨셉(c)”을 사용해 이미지를 생성합니다.
   • 예: “Van Gogh” 스타일 이미지를 여러 장 샘플링.

2. 분산 모델 출력에서 컨셉 요소 추출 (Frozen Model)

1. Frozen Original SD($\theta^*$)에 제거 대상 컨셉(c)과 빈(또는 다른) 컨셉($c_0$)을 각각 넣어,
   • 두 가지 출력 $\epsilon_{\theta^*}(x_t, c, t)$와 $\epsilon_{\theta^*}(x_t, c_0, t)$를 얻습니다.
2. 이를 Classifier Guidance 방식처럼 빼줌으로써,
   • $\eta \Bigl[\epsilon_{\theta^*}(x_t, c, t) \;-\; \epsilon_{\theta^*}(x_t, c_0, t)\Bigr]$
   • 여기서 $\eta$는 가중치 계수입니다.

3. 학습할 모델($\theta$) 출력과의 비교

1. Fine-tune ESD($\theta$)에 같은 입력 $(x_t, c, t)$를 넣어,
   • $\epsilon_{\theta}(x_t, c, t)$를 구합니다.
2. 동결된 모델에서 구한 “(제거 대상 컨셉만 골라낸) 출력”을 뺀 결과와
   • 학습 중인 모델의 결과가 유사(L2 Loss 최소)하도록 학습을 진행합니다.
   • 즉,
     $\mathcal{L} = \bigl\| \epsilon_{\theta}(x_t, c, t) \;-\; \bigl(\epsilon_{\theta^*}(x_t, c, t) - \eta[\epsilon_{\theta^*}(x_t, c, t) - \epsilon_{\theta^*}(x_t, c_0, t)]\bigr) \bigr\|^2$

4. 효과

• 학습 후에는 모델((\theta))이 “Van Gogh”처럼 제거된 컨셉을 표현하지 못하도록(잊어버리도록) 유도됩니다.
• 동시에 나머지(제거 대상이 아닌) 표현 능력은 그대로 유지하려는 목적을 달성합니다.

7.2 Unified Concept Editing in Diffusion Models

이 논문에서는 원치 않는 컨셉(예: “Van Gogh” 스타일)을 제거 또는 변형하면서도,
다른 중요한 컨셉(예: “art” 등)은 그대로 보존하는 방법을 제안합니다.

아이디어

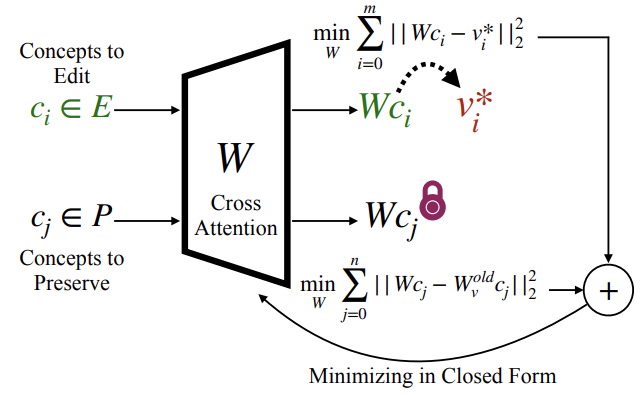
• $\mathbf{c_i}\in E$: 편집(제거) 대상인 컨셉
• $\mathbf{c_j}\in P$: 보존해야 하는 컨셉
• $W$: 크로스 어텐션(Cross Attention) 계층의 파라미터(또는 선형 변환 행렬)

편집 대상인 $\mathbf{c_i}$는 원하는 목표 벡터 $\mathbf{v}_i^*$와 유사하게 맞추되,
보존해야 할 $\mathbf{c_j}$는 기존 파라미터 $W^{\text{old}}$가 반영하던 결과와 크게 다르지 않도록 (파라미터 변화 최소화) 학습합니다.

수식

1. 첫 항: 제거(또는 수정)하고자 하는 컨셉($\mathbf{c_i}$)을
   • 목표 벡터($\mathbf{v}_i^*$)에 가깝도록 조정하는 항.
2. 둘째 항: 보존해야 하는 컨셉($\mathbf{c_j}$)은
   • 기존 모델 파라미터($W^{\text{old}}$)가 적용된 결과와 차이가 최소가 되게 함.

적용 예시

• $\mathbf{c_i} = \text{“Van Gogh”}$: 제거하고 싶은 화풍(스타일)
• $\mathbf{c_j} = \text{“art”}$: 예술성 관련 컨셉은 잃지 말아야 함
• 학습이 끝나면, “Van Gogh” 스타일은 사라지거나 변형되지만, “art”라는 일반적인 컨셉은 그대로 유지됩니다.