🌈 이번글에 대한 소개
- 이번 글에서는 Feed Forward Netowrk의 의미, 구조, activation function, loss function, backpropagation 과정에 대한 내용을 포스팅하려고 합니다. 부족한 점에 아낌없는 조언 부탁드립니다. 감사합니다. 😀
📙Feed Forward Neural Network에 대한 소개
- Deep Feed Forward Network는 feedforward networks또는 multi-layer-perceptrons(MLPs)라고도 불리며 딥러닝의 기본이 되는 Network구조입니다.
📌feedforward network를 학습한다는 것의 의미
- feedforward Network를 학습한다는 것은 🌈최적의 🌸함수 를 찾는 것입니다. 여기서 🌈최적의 기준은 loss function 이며 🌸함수를 조금 더 구체적으로 표현하면 각 Network Layer안에 존재하는 파라미터 입니다.
- 정리하면, "feed-forward network를 학습한다는 것은, 주어진 조건(입력 데이터와 출력 데이터)에 대해서 loss function의 값을 가장 작게하는 각 Network안의 파라미터들을 찾는 과정이다."로 요약해볼 수 있습니다.
- 간단하게 모델을 만들어보고 각 Network Layer안에 존재하는 파라미터가 무엇인지 살펴보겠습니다.
💻 Python Code
import tensorflow as tf
from tensorflow.keras.layers import Dense, Input
inputs = Input(shape=(5, ))
x = Dense(10, activation='relu')(inputs)
x = Dense(5, activation='relu')(x)
x = Dense(1, activation='softmax')(x)
model = Model(inputs=inputs, outputs=x)
print('model Layer', model.layers, sep='\n')
hidden1 = model.layers[1]
weight1, bias1 = hidden1.get_weights()
print(f'weight1 shape : {weight1.shape}, bias1 shape : {bias1.shape}')
print('wieght1', weight1, sep='\n')
output
model Layer
[<keras.engine.input_layer.InputLayer object at 0x7f70213a7370>,
<keras.layers.core.dense.Dense object at 0x7f70213a7310>,
<keras.layers.core.dense.Dense object at 0x7f70213a74f0>,
<keras.layers.core.dense.Dense object at 0x7f70213a7a00>]
weight1 shape : (5, 10), bias1 shape : (10,)
wieght1
[[-0.627294 -0.39816856 -0.4012763 -0.12288213 -0.25013116 -0.6287098
-0.25649098 -0.50557864 0.23613864 0.53828317]
[ 0.07167685 -0.35622233 0.30352753 0.6170072 -0.41132867 0.5323997
-0.28512043 -0.14471084 -0.43009242 0.0347147 ]
[ 0.40997368 -0.2367732 -0.4710493 -0.0296613 0.3623855 0.00384152
0.58090895 0.3905664 -0.1727534 0.42306823]
[-0.3712097 -0.39768845 0.5205744 0.35090762 -0.3273296 0.1901626
0.40312773 -0.07252026 -0.336823 0.06312424]
[ 0.00865048 -0.585642 0.4946553 0.29103947 -0.4843334 -0.05296242
0.43102235 0.60352653 -0.59478116 0.08563918]]
- tensorflow로 모델 구조를 생성하게 되면 network Layer가 생성되고 각 Layer안에 파라미터가 초기화 됩니다. 이 파라미터들이 우리가 학습을 통해서 최적의 값을 찾아야 하는 대상이 됩니다.
📌y=f(x)와 y=f(x;θ)의 차이
-
저는 두 함수의 차이가 "주어진 함수에 대해서 원하는 값 찾기" 와 "주어진 값에 대해서 최적의 함수를 찾기" 라는 차이가 있다고 생각합니다.
-
예를들어, y=2x와 같은 함수가 주어졌을 때, x=1일때 y=2×1=2 와 같이 정의역 x에 대해 치역 y를 찾는 문제나, y=2가 주어졌을 때 f−1(2)=1와 같이 역함수를 통해 치역 y가 주어졌을 때 정의역 x를 찾는 문제를 풉니다.
-
즉, 함수 f=2x로 주어진 상황에서 정의역 또는 치역이 주어지면 원하는 값을 찾는 과정이라고 할 수 있습니다.
y=f(x;θ)
-
하지만, MLP에서는 입력값 x가 주어졌을 때 출력값 y를 잘 mapping 해주는 최적의 파라미터 θ를 찾는 것을 목표로 합니다.
-
즉, y=θx에서 2=θ×1를 만족하는 θ를 찾는 과정입니다.
📌왜 'feed-forward'인가?
f(x)=f(3)(f(2)(f(1)(x))))
- Multi-Layer-Perceptron의 이름에서 알 수 있듯이 여러개의 층을 쌓아서 모델을 생성합니다.
x(0)→f(1)→x(1)→f(2)→x(2)→f(3)→y
- x(0) 이 y로 진행되는 과정에서 feedback없이 앞으로 직진하기 때문에
feed --> forward라고 불립니다.
- 하지만, 자연어 처리, 시계열 데이터는 입력 데이터들 사이의 순서 or 연관 정보가 있기 때문에 훈련 정보에 대한 feed back이 필요했습니다. 이런 구조적 문제를 개선하고자 feedback connection을 추가한 Recurrent Neural Network(RNN) 구조가 파생되었고 자연어 처리, 시계열 데이터 분야에서 많이 사용하게 됩니다.
📙Feed Forward Network의 구조
📌Network Layer는 Unit들의 모임이다
👿 가중치 W(nxm) 에 대한 표기 및 위치는 참고 도서마다 달라서 선형변환의 의미에 부합하고 일관되도록 수정하여 작성하겠습니다.
👿 위에서 출력한 tensorflow Layer의 shape을 transpose 취한 것을 W로 표기하고자 합니다.
- MLP 각 Layer는 하나의 "함수" 또는 '선형변환' 으로 이해해볼 수 있습니다.
MLP:f(2)(f(1)(x))=f(2)(f(1)(x;W(1),c);W(2),b) =f(2)(h(1);W(2),b)=y f(2)(f(1)(x))=f(x;W(1),c,W(2),b)
- 이렇게 함수로 표현해볼 수 있습니다. 또한 MLP를 선형변환 함수(Matrix, Vetor-to-Vector function) 으로 구조화하면 아래와 같습니다.
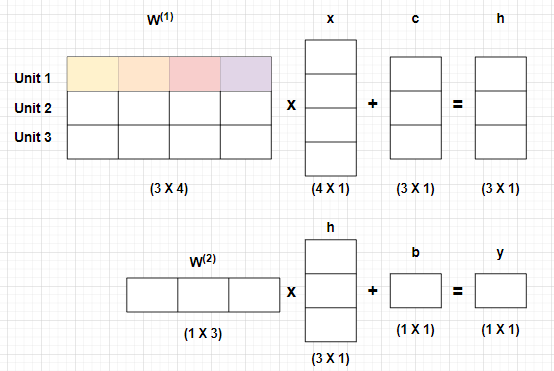
-
가중치 W(1)과 W(2)는 x(vector)를 h(vector)로 h(vector)를 y(vector)로 변환 시켜주는 선형변환 함수입니다.
Rather than thinking of the layer as representing a single vector-to-vector function,
we can also think of the layer as consisting of many units that act in parallel,
each representing a vector-to-scalar function. - DeepLearning (Ian Goodfellow, Yoshua Bengio, Aaron Courville)
-
하지만 책에서는 Vector to Vector function으로 바라보기 보다는, 각 Layer는 Vector-to-scalar function 의 역할을 하는 Unit들의 모임 이라는 관점으로 보아야 한다고 합니다. 다음의 관점에 대해서 이해해보고자 합니다.
-
3차원의 입력벡터 X(x1,x2,x3)를 Layer(W)에 입력하여 출력벡터 Y(y1,y2)를 생성하고자 합니다. 이때 Layer에서는 선형변환이 일어나며 구조를 보면 아래와 같습니다.
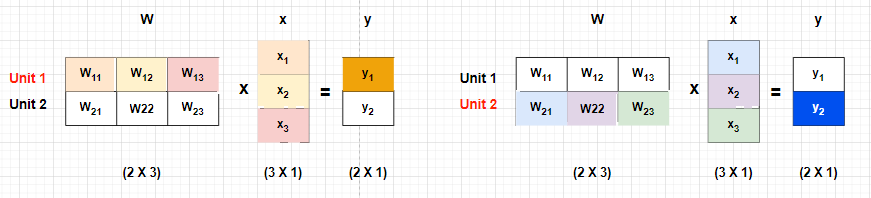
Unit1:y1=W11x1+W12x2+W13x3
Unit2:y2=W21x1+W22x2+W23x3
Uniti:yi=Wi1x1+Wi2x2+Wi3x3
-
Layer안의 파라미터 Martix에서 i번째 행(vector)은 출력벡터의 i번째 요소(scalar)의 값을 구하는데 사용됩니다. 각 행은 하나의 unit으로 대변되고, 각 유닛은 Vector-to-scalar변환을 하는 함수로 해석할 수 있습니다.
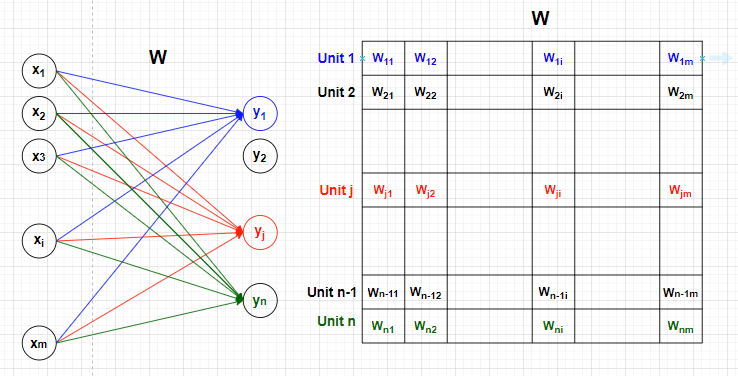
-
입력벡터 x에 대해 Unitj가 활성화되면 출력벡터의 j번째 element값이 생성됩니다. 또한 Layer의 Matrix j행 i열의 값 Wji는 오직 입력벡터 x의 i번째 요소와 출력벡터 y의 j번째 요소 사이의 관계를 설명할 때만 사용됩니다. 즉, 선형변환 Matrix의 Wji는 xi가 yj에 영향을 미치는 정도 라고 할 수 있습니다.
-
따라서, 뒤에서 나올 Backpropagation과정에서 가중치를 업데이트 할 때의 수식과 그에 따른 해석은 아래와 같습니다.
Wji(l)=Wji(l)−α∂Wji(l)∂J(W,b)
-
Wji(l) : lth Layer의 xi가 yj에 영향을 미치는 정도
-
∂Wji(l)∂J(W,b) : Wji(l)을 살짝 바꿔봤을 때 목적함수 J(W,b)는 어떻게 변하나?(편미분)
-
Wji(l)−α∂Wji(l)∂J(W,b) : J(W,b)가 Convex하다는 가정하에 J(W,b)가 작아지는 방향으로 Wji(l)를 ∂Wji(l)∂J(W,b)에 일정 비율(α)만큼 업데이트하자.
-
정리하면, 입력벡터의 크기가 m이고 출력벡터의 크기가 n일 때 Layer의 선형변환 Matrix의 구조는 n×m이며, i번째 행(Uniti)는 출력벡터의 i번째 요소(element)값을 구하는데 사용된다. 따라서, Layer 자체로 보면 Vector-to-Vector function으로 해석할 수 있지만, Vector-to-Scalar function으로 구성된 unit들의 모임으로 접근하는 것이 좋다.
📙Activation Function
-
딥러닝 알고리즘에서 각 층을 선형변환한 후 하나의 비선형 활성화 함수를 더해 다층 네트워크가 단층 선형함수와 동일하게 되는 것을 피할 수 있고, 그로 인해 더 강력한 적합 능력을 갖출 수 있습니다.
f2(f1(x))=f(2)(W(b×a)(1)X(a×1))
=W(c×b)(2)W(b×a)(1)X(a×1)
=(W(c×b)(2)W(b×a)(1))X(a×1)
=W(c×a)X(a×1)
-
행렬연산에 의해 다층 선형변환이 단층 선형변환으로 대체될 수 있음을 알 수 있습니다. 즉, 선형변환으로만 이루어져 있다면 여러층의 복잡한 구조를 쌓아도 단층 선형 변환으로 대체될 수 있고 모델 적합능력을 향상시키는 것에 한계가 발생합니다. 따라서, 이런 문제점들을 개선하고자 선형변환 이후 비선형 함수의 activaion function을 사용하게 되었습니다.
📌Activation function을 추가한 구조
- activation function g(z)를 추가한 수식은 아래와 같습니다.
FirstLayer:h(1)=g(1)(W(1)x+b(1))SecondLayer:h(2)=g(2)(W(2)h(1)+b(2))
- 또한, 이를 구조화 하면 아래와 같습니다.
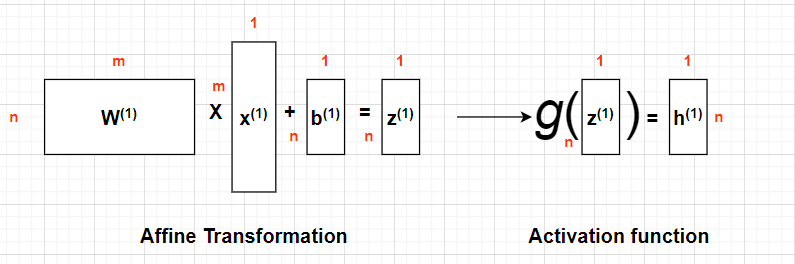
📌대표적인 활성화 함수
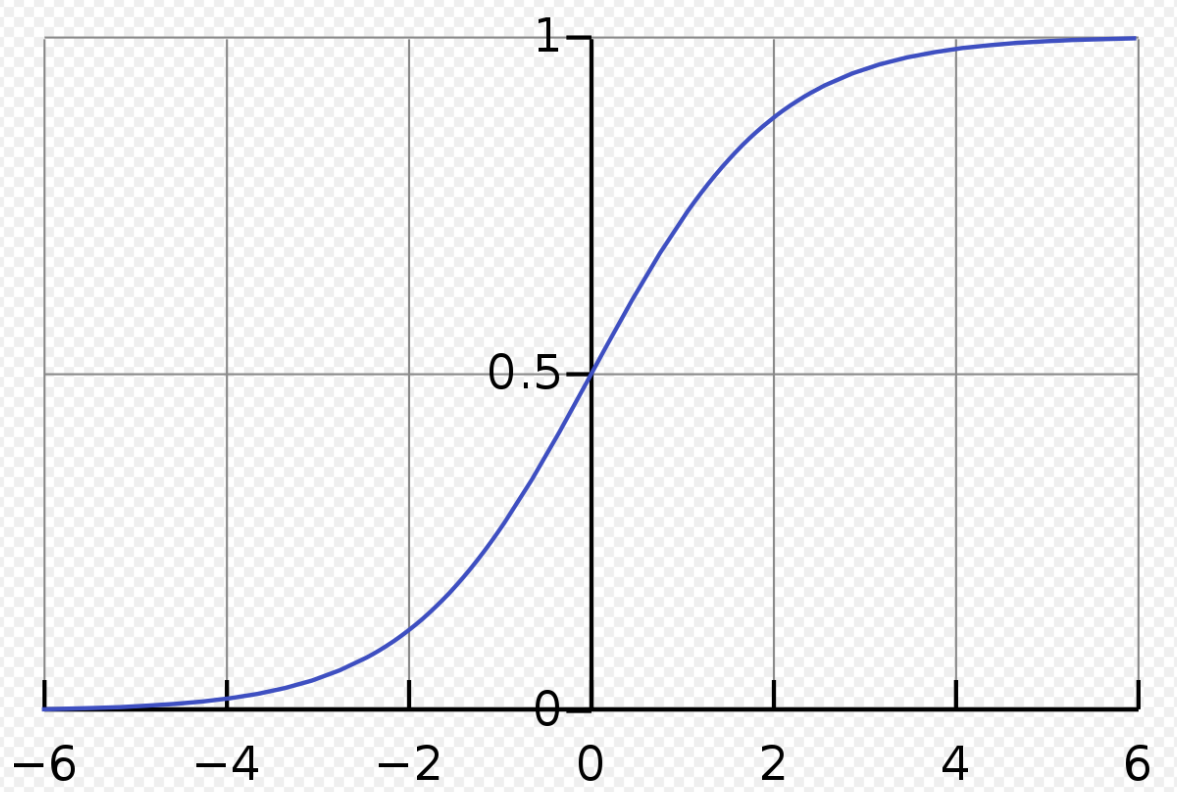
- 활성화함수로 자주 사용되는 함수에는 Sigmoid, HyperbolicTangent, RectifiedLinearUnit(ReLU)가 있습니다. 먼저 Sigmoid, HyperbolicTangent에 대해서 살펴보겠습니다. 또한, Backpropagation과정에서 사용되는 도함수도 같이 구해보고자 합니다.
| Sigmoid | HyperbolicTangent |
|---|
 출처 : wikipedia 출처 : wikipedia | 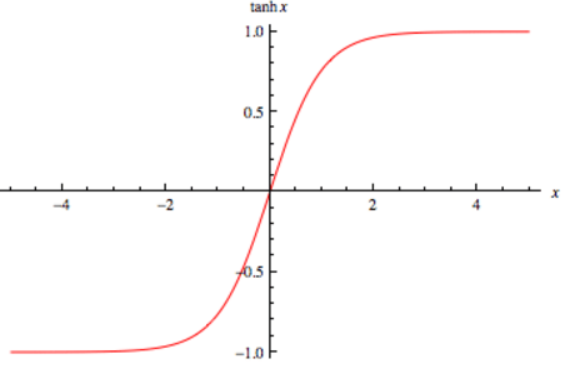 출처 : i2tutorials 출처 : i2tutorials |
Sigmoid:g(z)=1+exp(−z)1Tanh:g(z)=tanh(z)=e(z)+e(−z)e(z)−e(−z)
Sigmoid:g′(z)=g(z)(1−g(z))Tanh:g′(z)=1−(g(z))2
🌈gradient vanishing 문제 발생과 해결
| Sigmoid | HyperbolicTangent |
|---|
| z가 크다면 : f(z)→1,f′(z)→0 | z가 크다면 : f(z)→1,f′(z)→0 |
| z가 작다면 : f(z)→0,f′(z)→0 | z가 작다면 : f(z)→−1,f′(z)→0 |
- Sigmoid와, HyperbolicTangent는 딥러닝 초기에 주로 사용되던 activationfunction입니다. 출력층 z의 크기가 점점 커지거나 작아지면 f′(z)는 0에 수렴합니다. 0에 수렴하게 된 f′(z)는 Backpropagation으로 전달되는 그라디언트를 0에 가깝게 만들어 gradientvanising문제를 야기합니다.
- 이런 문제를 ReLU(RectifiedLinearUnit)이라는 활성화 함수를 통해 해결하였습니다.
📌ReLU계열의 활성화 함수
- ReLU는 단측면에 대해서 정보를 전달하는 비선형 함수 구조를 통해 gradientvanishing문제를 효과적으로 해결하였습니다.
| ReLU(RectifiedLinearUnit) | LeakyReLU |
|---|
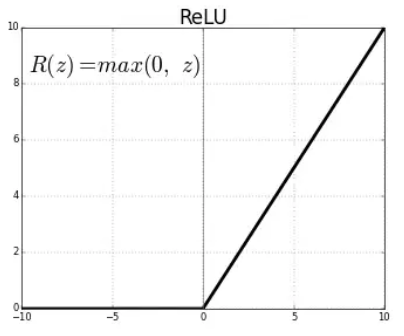 | 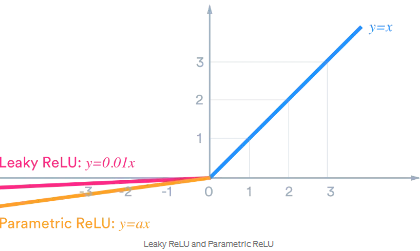 |
| g(z)=max(0,z) | g(z)=max(0,z)+α∗min(0,z) |
| g′(z)=1(z>0),0(z⩽0) | g′(z)=1(z>0),−α(z⩽0) |
| 이미지 출처 : medium - Himanshu S | |
🌈ReLU계열 활성화 함수의 장단점 비교
- ReLU는 sigmoid, tanh와 비교하면 다음과 같은 장점을 가지고 있습니다.
- 계산적 관점에서 ReLU활성화 함수는 하나의 임계치만 있으면 활성화 값을 얻을 수 있으므로 sigmoid, tanh에 비해 계산 복잡도가 낮음
- ReLU sigmoid, tanh에 비해 더 넓은 활성화 영역을 제공하며 gradientvanishing문제를 효과적으로 해결
- ReLU의 단측면 억제가 네트워크의 희소 표현 능력을 제공
🌈ReLU의 한계점과 LReLU
- ReLU의 희쇼표현 능력은 단점이 되기도 합니다.
- 순전파 과정에서 Network의 출력값 z가 0 이하라면 ReLU Unit을 통화한 이후 0이 되어 이후로 정보가 전달되지 않습니다. 즉, 뉴런들이 죽는 문제가 발생합니다.
- 음의 정보에 대해 일정부분 정보를 전달할 필요성을 느꼈고 이를 반영한 활성화함수로 LeakyReLU(LReLU)가 고안되었습다.
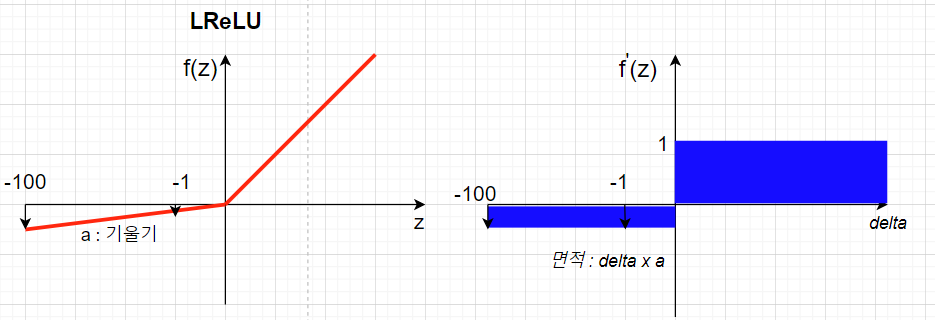
- LReLU에서는 일반적으로 α를 작게 설정하여 음의 출력값에 대해서 정보를 전달하기는 하지만 많이 전달하지 않습니다.
- α를 작게 설정함으로서 z(순전파)와 δ(역전파)의 값이 작다면 정보의 전달이 거의 없는 단측면 억제를 구현하는 동시에 전달하려는 정보가 유의미하다면 (매우 큰 음의값) 정보를 전달하는 역할을 해주게 됩니다.
🌈Leaky ReLU의 파라미터 a의 문제점과 개선방법
-
LReLU에서 파라미터 α는 모델 설계자의 경험적 판단에 의해서 설정됩니다. 즉, 튜닝해야하는 파라미터가 1개 더 추가되어 모델 설계의 난이도를 증가 시킵니다. 난이도의 증가 문제와 모델 설계자의 경험적 판단에 기인한 과적합 문제를 해결하고자 α를 설정하는 기능이 추가된 PReLU와 RReLU가 고안됩니다.
-
ParameticReLU(PReLU)
- 기울기 α를 네트워크 중에서 학습가능한 파라미터로 설정하여 Backpropagation 과정에서 다른 네트워크와 함께 훈련
-
RandomReLU(RReLU)
- 훈련중에 α를 랜덤 샘플로 설정하고, 테스트 때 다시 고정함으로서 일정정도의 정규화 기능을 추가함
📌다른 활성화 함수
- ReLU는 sigmoid, tanh이외에도 여러 활성화 함수가 존재합니다. 많이 사용하지는 않지만 특정 Task에서는 좋은 효과와 장점을 가지고 있다고 합니다. 일반적으로 미분가능한 함수(Differentiablefunction)들이 좋은 효과를 보인다고 합니다.
추가 활성화 함수
Cosine:h=cos(Wx+b)
Softmax:hi=softmax(zi)=∑jexp(zj)exp(zi)
RadialbasisfunctionorRBFunit:hi=exp(−σi21∥Wi−x∥2)
Softplus:g(a)=ξ(a)=log(1+e(Wx+b))
Hardtanh:g(a)=max(−1,min(1,Wx+b))
- 위와 같이 자주 사용하지 않지만 다양한 활성화 함수가 존재합니다. cos을 활용한 주기적 성질, 거리의 개념을 적용한 방식 등이 인상 깊었습니다. 추후 기회가 된다면 각 함수에 대해서 고찰하는 시간을 갖겠습니다.
📌활성화 함수에 대한 고찰
- Activation function을 공부하며 고찰한 내용과 추후 공부에서 확장시키면 좋을 내용들을 적고자합니다.
🌈 Differentiable function
-
gradient방식으로 모델을 학습하게 되면 backpropagation 과정에서 활성화 함수의 미분값을 사용합니다. 따라서 활성화 함수들은 '미분 가능' 해야 하는 것이 이론적으로 타당해 보입니다.
-
하지만 ReLU 는 z=0인 점에서 우극한과 좌극한이 다르기 때문에 미분가능하지 않습니다.
z→0+limz−0f(z)−f(0)=1z→0−limz−0f(z)−f(0)=0
-
하지만, 컴퓨터 연산과정에서 딱 0으로 값이 떨어지지 않고 0에 매우 가깝게 연산됩니다. 이런 상황들을 관찰하여 "heuristicallyjustified"(경험적으로 정당화)하여 ReLU와 같은 Activationfunction을 사용할 수 있게 됩니다.
-
즉,Network의 학습은 반복법(iterativemethod)을 통해 진행되므로 '미분 가능' 이라는 조건을 정의역의 모든 구간에서 만족시킬 필요는 없습니다.
🌈 정보 전달량의 규제
👿 설명을 위해 작성한 모식도는 실제 분포와 다릅니다.
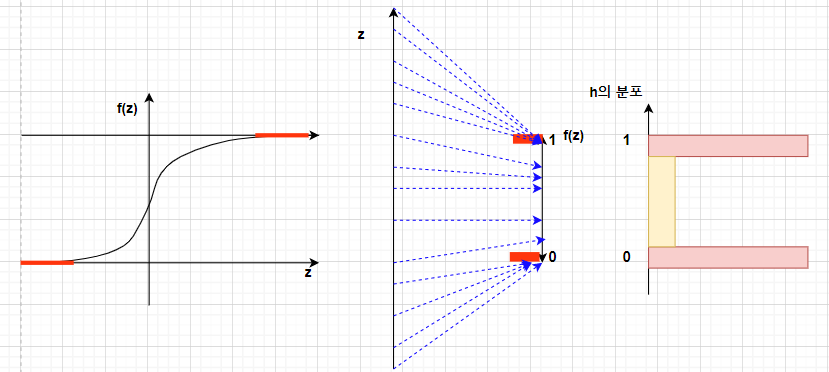
- tanh, sigmoid 활성화 함수의 목적은 "비선형함수를 사용하여 모델의 적합력을 높이는 것" 뿐만아니라 "출력값의 크기가 커지는 것을 막아 정보 전달량에 대한 규제를 하는 것"도 있다 라는 생각이 들었습니다.
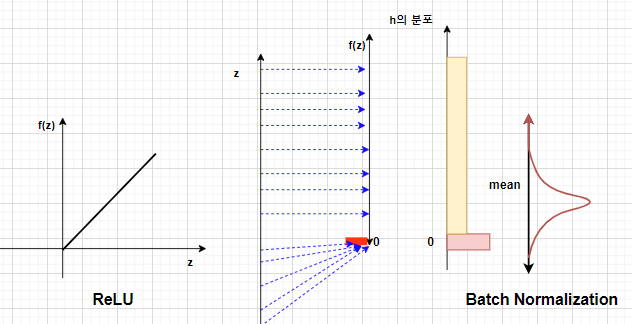
- sigmoid, tanh의 gradientvanishing문제를 개선하고자 ReLU라는 활성화 함수가 만들어 졌지만, 양의 출력값에 대해서는 정보전달량에 대한 규제를 하지 못합니다.
- 이런 ReLU의 문제점을 BatchNormalization이 해결하여 좋은 효과를 보았고, sigmoid의 상위 호환 개념이 ReLU와 BatchNormalization의 조합이지 않을까 라는 생각을 해봤습니다.
📙Output Units
- Output Layer는 이전 Layer들에 의해 출력된 값을 모델 학습 목표에 맞는 적절한 형태로 변환해주는 역할을 합니다. 따라서 적절한 형태의 activation function을 선택해야 합니다. output layer에서 선택한 activation function은 뒤에 나올 Objective function(목적 함수)와 밀접한 관련이 있습니다.
| Objectivefunction | activationfunction |
|---|
| MSE | 예측치에 근접한 값을 출력하는 상황에서는 sigmoid와 tanh같은 범위가 정해져 있는 비선형함수를 사용하지 않고 선형변환을 사용합니다. |
| BinaryCrossEntropy | 이진 분류 문제에서는 output layer의 activation function으로 sigmoid 함수를 사용합니다. |
| CrossEntropy | 다중 분류 문제에서는 output layer의 activation function으로 softmax 함수를 사용합니다. |
-
softmax를 사용한다는 것은 출력값 y의 모든 요소들의 합을 1로 만들어주며 "확률의 개념으로 접근하겠다" 라는 의미를 가진다고 생각합니다. 확률이라는 것은 추상적인 것이기 때문에 이것을 수치화 하기 위해서는 연산이 가능해야 하고 "다중 클래스의 분포 확률"이라는 확률 개념을 잘 표현할 수 있는 수식이 softmax이기 때문에 softmax를 사용한다. 라고 생각합니다.
yi=softmax(zi)=∑jexp(zj)exp(zi)
-
따라서 softmax 값으로 출력된 y에서 가장 큰 yi는 Classi가 정답이 될 확률이 높다는 것을 의미하게 됩니다.
-
ML/DL에 존재하는 확률 개념들은 실제 연산을 위해서 수학이라는 표음문자로 대변되어야 한다고 생각합니다. 이 부분에 대해서는 계속 공부하며 정립해 나가도록 하겠습니다.
📙Objective function
- feedforward Network를 학습한다는 것은 🌈최적의 🌸함수 를 찾는 것입니다. 여기서 🌈최적의 기준은 loss function 이며 🌸함수를 조금 더 구체적으로 표현하면 각 Network Layer안에 존재하는 파라미터 입니다.
- Backpropagation과정의 가중치를 업데이트 수식입니다.
Wji(l)=Wji(l)−α∂Wji(l)∂J(W,b)
- Wji(l)−α∂Wji(l)∂J(W,b) : J(W,b)가 Convex하다는 가정하에 J(W,b)가 작아지는 방향으로 Wji(l)를 ∂Wji(l)∂J(W,b)에 일정 비율(α)만큼 업데이트하자.
-
objective function은 모델의 학습 목표가 되는 함수 입니다. 모델 학습에 의해 출력된 결과가 최소(or 최대)가 되도록 반복법과 경사하강법을 통해 Network의 파라미터를 업데이트 하게 됩니다. 예측 값이 출력값에 근사해야 한다면 MSE가 최소가 되는 방향으로, 이진 분류와 다중분류는 각각 BinaryCrossEntropy와 CrossEntropy가 최대가 되는 방향으로 모델 파라미터를 업데이트 합니다.
-
L2 정규항을 추가한 MSE, BinaryCrossEntropy, CrossEntropy를 전개해보고 다음 Backpropagation에서 사용하도록 하겠습니다.
📌loss function 전개
🌈기호
-
m개의 샘플이 포함된 결합 : {(x(1),y(1)),(x(2),y(2)),...,(x(m),y(m))}
x(Sl−1×1)(l)=a(l−1)(z(Sl−1×1)(l−1))
z(Sl×1)(l)=W(Sl×Sl−1)(l)x(Sl−1×1)(l)+b(Sl×1)(l)
-
a(l−1): l−1thLayer의 활성화 함수
-
x(Sl−1×1)(l) : lthLayer의 입력 벡터
-
W(Sl×Sl−1)(l) : lthLayer의 선형변환 함수
-
b(Sl×1)(l) : lthLayer의 편향 벡터
-
z(Sl×1)(l) : lthLayer의 출력 벡터
🌈 제곱오차의 비용함수
J(W,b)=[m1i=1∑mJ(W,b;x(i),y(i))]+2λl=1∑Ni=1∑Sl−1j=1∑Sl(Wji(l))2=[m1i=1∑m∥∥∥∥y(i)−LW,b(x(i))∥∥∥∥2]+2λl=1∑Ni=1∑Sl−1j=1∑Sl(Wji(l))2
🌈 이진분류에서의 교차 엔트로피 손실함수
J(W,b)=[m1i=1∑mJ(W,b;x(i),y(i))]+2λl=1∑Ni=1∑Sl−1j=1∑Sl(Wji(l))2=−[m1i=1∑m{y(i)lno(i)+(1−y(i))ln(1−o(i))}]+2λl=1∑Ni=1∑Sl−1j=1∑Sl(Wji(l))2
- 예측 클래스 o(i)와 실제 클래스 y(i) 사이의 교차엔트로피
- y(i)와 o(i) 같을 경우 최대 엔트로피 값을 갖습니다.(손실함수가 최소)
🌈 다중분류의 비용함수
J(W,b)=[m1i=1∑mJ(W,b;x(i),y(i))]+2λl=1∑Ni=1∑Sl−1j=1∑Sl(Wji(l))2=−[m1i=1∑mk=1∑nyk(i)lnok(i)]+2λl=1∑Ni=1∑Sl−1j=1∑Sl(Wji(l))2
- ok(i) : i번째 샘플의 예측이 클래스 k에 속할 확률
📙Backpropagation
-
ML/DL은 반복법과 경사하강법을 이용하여 모델을 업데이트 합니다. 여기서 모델을 업데이트 한다는 것은 네트워크 내부의 파라미터들을 업데이트 한다는 것 입니다. 따라서, 파라미터를 "어떻게 업데이트 할지" 결정해야 하고 이를 "목적함수가 최소가 되는 방향"으로 설정합니다.
-
따라서 목적함수의 값을 얻어야 하고 이 과정이 순전파 과정입니다. 그리고 목적함수의 값을 통해서 "목적함수가 최소가 되는 방향"으로 파라미터를 업데이트 하는 과정이 역전파 과정, Backpropagation입니다.
-
점화식으로 구성된 잔차식을 구하고, 출력 레이터의 잔차를 계산하여 전체 업데이트 계산 공식을 유도하겠습니다.
📌잔차 점화식 전개
-
∂zj(l)∂J(W,b)는 l층의 j번째 노드를 움직였을 때 손실함수가 변하는 정도 즉, 잔차량으로 간주할 수 있고 ∂j(l)로 표현합니다.
-
우선 이 잔차 ∂j(l)들의 점화식을 구하고 마지막 층의 잔차 ∂(L)를 목적함수에 기반하여 구하여 점화식을 완성하겠습니다.
-
lthLayer 가중치와 편향의 업데이트 수식입니다.
Wji(l)=Wji(l)−α∂Wji(l)∂J(W,b)bj(l)=bj(l)−α∂bj(l)∂J(W,b)
-
여기서 각 파라미터를 얼마나 업데이트 할지를 대변하는 값이 ∂Wji(l)∂J(W,b), ∂bj(l)∂J(W,b)이므로 이것의 값을 구하는 것이 시작점 입니다.
-
l 층의 출력 노드 zj(l)는 출력 층 사이의 존재하는 은닉층을 통과합니다. 그리고, 다음 은닉층에 입력될때 다음 은닉층의 모든 노드에 동일하게 입력됩니다. 따라서, zj(l)로 표현된 ∂zj(l)∂J(W,b)를 zj(l)와 다음 은닉층들의 노드들을 고려하여 표현해 볼 수 있습니다.
∂zj(l)∂J(W,b)=k=1∑Sl+1(∂zk(l+1)∂J(W,b)∂zj(l)∂zk(l+1))
- 이 과정을 통해 현재 층(l)의 node j와 다음 층(l+1)의 node k 사이의 관계를 설명하는 점화식을 얻을 수 있습니다.
∂zj(l)∂zk(l+1)=∂zj(l)∂(∑j′SlWkj′(l+1)xj′(l+1)+bk(l+1))=Wkj(l+1)f′(zj(l))
- ∂zj(l)∂J(W,b)는 l층의 j번째 노드를 움직였을 때 손실함수가 변하는 정도 즉, 잔차량으로 간주할 수 있고 ∂j(l)로 표현합니다. 따라서, 점화식을 다음과 같이 나타낼 수 있습니다.
∂zj(l)∂J(W,b)=(k=1∑Sl+1Wkj(l+1)∂zk(l+1)∂J(W,b))f′(zj(l))∂j(l)=(k=1∑Sl+1Wkj(l+1)∂k(l+1))f′(zj(l))...(∗)
- 잔차 점화식을 통해 우리가 구하려고 한 ∂Wji(l)∂J(W,b), ∂bj(l)∂J(W,b)을 전개하겠습니다.
∂Wji(l)∂J(W,b)=∂zj(l)∂J(W,b)∂Wji(l)∂zj(l)=δj(l)xi(l)=δj(l)ai(l−1)
∂bj(l)∂J(W,b)=δj(l)
- 각 층의 파라미터를 잔차와, 출력값의 곱을 통해 업데이트 한다는 것을 구했습니다. 따라서 우리는, 마지막 층의 잔차 δ(L)을 계산한 후 점화식 (∗)을 통해 다른 층의 잔차 δ(L−1),δ(L−2),δ(L−3)......δ(2),δ(1)를 계산하여 파라미터를 업데이트 하면 됩니다.
📌목적 함수에 따른 마지막 항의 잔차 계산
- 목적함수에 따라 마지막 층의 잔차 δ(L)을 구하겠습니다.
- Batch와 정규항의 영향은 고려하지 않습니다.
🌈 제곱오차의 잔차
J(W,b)=21∥∥∥∥y−a(L)∥∥∥∥2=21∥∥∥∥y−f(zj(L))∥∥∥∥2δ(l)=−(y−a(L))f′(z(L))
🌈 Binary Cross Entropy의 잔차
J(W,b)=−lnak(L)δk(L)=−ak~(L)1⋅∂zk(L)∂ak~(L)
- k : 예측 클래스, k~ : 실제 클래스
🌈 Cross Entropy의 잔차
J(W,b)=−k=1∑nyklnak(L)=−k=1∑nyklnf(zk(L))
- k : 예측 클래스, k~ : 실제 클래스
- ak(L)=f(zk(L))일 때 소프트맥스 활성화 함수를 사용하면 마지막 항의 잔차는 다음과 같습니다.
δ(l)=ak(L)−yk={ak~(L)−1ak(L) if k=k~ if k=k~
📘Reference
- Deep Learning by lan Goodfellow, Yoshua Benjio, Aaron Courvile
- Mathematics for Machine Learning by A. Aldo Faisal, Cheng Soon Ong, and Marc Peter Deisenroth
- Elementary Linear Algebra with Supplemental Applications by Chris Rorres and Howard Anton
- Hulu 데이터 과학팀, "데이터 과학자와 데이터 엔지니어를 위한 인터뷰 문답집", 제이펍, (2020.06.30)
- 조영수,강주호,박동완, "해석학", 경문사, (2007.02.28)
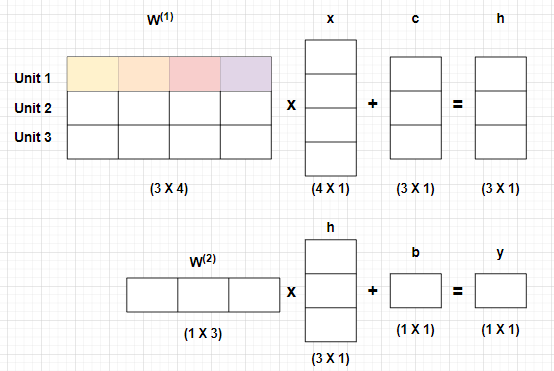



 출처 : wikipedia
출처 : wikipedia 출처 : i2tutorials
출처 : i2tutorials



