3. Neural Networks - MLP

Daisy 🌼·2022년 7월 11일

Deep learning 기초

목록 보기

3/10

학습목표

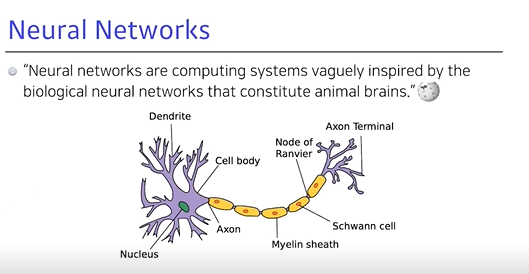
신경망(Neural Networks)의 정의, Deep Neural Networks에 대해 학습

신경망(Neural Networks)간단한 Linear neural networks 를 예시로, Data, Model, Loss, Optimization algorithm 정의

Deep Neural Netoworks란 무엇이며 Multi-layer perceptron와 같이 더 깊은 네트워크 구성에 대한 학습

1. Neural Network

Neural Networks : 간단한 Linear neural networks를 예시로 Data, Model, Loss, Optimization algorithm 을 정의

💡 Deep Neural Networks 무엇이며 Multi-layer perceptron와 같이 더 깊은 NN는 어떻게 구성할까?

Neural Networks (뇌신경망)
- 인간의 뇌를 모방했지만 역전파를 활용 (역전파는 인간의 뇌에서는 일어나지 않음)
→ 따라서, 인간의 뇌를 모방한다고 딥러닝이 잘 된다는 해석은 애매함 (현 시각)
→ 수학적 방법 등이 더 합당하다고 설명할 수 있음

인간이 날고싶은 욕망 → 새를 모방한 기계 → Avion 3 → 라이트형제의 비행기
→ 현재 : 전투기 등 → 하지만 F-22는 새처럼 생기지 않음

Neural Networks 정의 (이하, NN)

단순히, 수학적 용어로 이미지라는 tensor가 주어지고 라벨이라는 벡터가 나오는 모델이 있다면, 우리가 찾고자 하는 NN은 모델을 내가 정의한 함수에 근사함

행렬의 비선형 연산이 반복적으로 일어나는 모델을 NN이라고 부를 수 있음

2. Linear Neural Networks

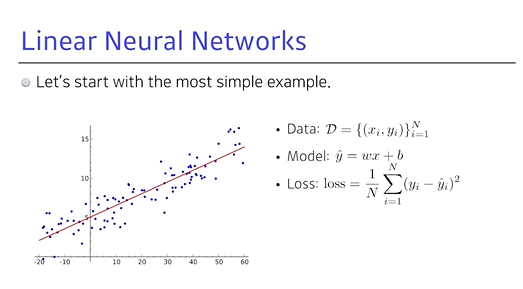
선형회귀 : 입력, 출력이 1차원인 문제가 있을 때 두 개를 연결하는 모델을 찾는 것으로, line에 대한 절편, 기울기를 통해 2개의 파라미터를 찾는 것

Data : 1차원 x, y가 있고, n개가 모여있는 데이터

Model : x에 스칼라 w (가중치 : weight)를 곱하고, b (편향 : bias)를 더함으로써 모델을 만듦 ( $\hat y =wx + b$ )
→ x에서 $\hat y$ 으로 가는 맵핑을 찾는 것을 목표로, 선형으로 한정짓고 선형 모델을 정의하는 w와 b를 찾는 것이 목적 (딥러닝으로 가면 수십 억 개의 파라미터를 찾아야 함)

Loss : 우리가 이루고자 하는 현상이 이뤄졌을 때 줄어드는 함수, 간단한 회귀문제를 풀 때 Loss function은 제곱을 사용
→ Yi는 y의 i번째 데이터를 출력하는 것이고, Y $\hat i$ 은 Xi를 집어넣었을 때 현재 모델의 출력 값
→ 결국 목표는 n개의 데이터를 잘 설명하고 표현할 수 있는 모델을 찾는 것으로, NN의 출력 값과 데이터 그 사이의 차이를 줄이는 것이 중요

w와 b의 analytic function이 존재, 바로 w와 b의 최적화(loss 최소화)하는 w, b를 찾을 수 있음

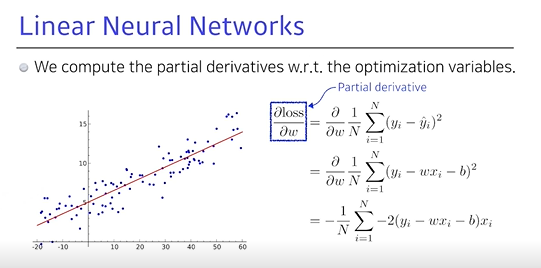
Loss function이 주어졌을 때, 이를 줄이는 게 목표
→ 파라미터가 어느 방향으로 움직였을 때 Loss function이 줄어드는지를 찾고, 그 방향으로 파라미터를 바꾸어야 함

Loss function을 각각 파라미터로 미분하게 되는 방향을 역수(음수) 방향으로 파라미터를 업데이트하게 되면, loss가 최소화되는 어떤 지점에 이르게 됨

n개의 데이터를 모두 사용했을 때, 그 출력값(학습 데이터의 타겟 데이터)과 모델의 아웃풋 사이의 제곱을 최소화하는 Loss function에 대한 w의 편미분

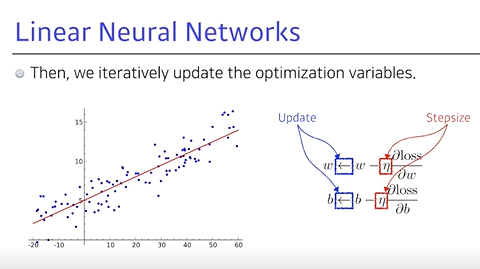
Loss function을 w로 편미분하는 값을 찾아, w에 이 편미분 값(적절한 값)을 곱하고 빼서 업데이트

w에 대해 편미분을 구하고, b에 대해 편미분을 구한 뒤 각각 특정 stepsize만큼 편미분 값을 곱한 후 빼줘서 업데이트

경사하강법 (gradient descent)

새로운 w에 편미분 값 stepsize delta를 곱하고, b도 마찬가지이며,
이런 식으로 w, b를 계속 업데이트 하는 방법

또한, 줄이고자하는 Loss function에 대해서 w, b라는 파라미터에 대한 편미분을 구하고, 이 편미분의 loss를 줄이는 것이 목적이기 때문에, 편미분을 빼서 최소값을 찾는 것

반면, Loss function이 아닌 Reward function이라 키우게 된다면, 경사상승법 (gradient ascent)라고 불림

업데이트해서 얻어지는 w와 b가 내 모델의 파라미터, 반면 모델이 선형으로 늘 예쁜 형태가 아님

레이어가 여러 개 쌓이고 가장 최종 Loss function 값을 전체 파라미터를 다 미분해야하는 것이 (...functionㅠㅠ → 10번 넘게 들어도 안 들렸음 ㅠㅠ)

각 파라미터만의 편미분을 업데이트 시키는 것이 regradient descent

eta라는 stepsize는 너무 커지게 되면 학습이 안 되기 때문에 중요함

gradient 정보는 결국 local(국소)한 정보로 위치에서 조금 밖에 유효하지 않기 떄문에,
stepsize를 너무 키워도 학습이 안 되고, 0에 가까워도 학습에 안 돼 적절한 stepsize를 찾는 것이 중요

optimization 방법론 중 adaptor learning은 stepsize를 자동을 바꿔줌 (나중에 배우게 될 것)

세상은 선형으로만 이뤄지지 않음
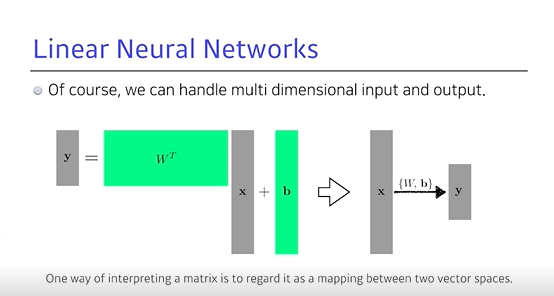
예를 들어, 100차원 입력해서 20차원 출력으로 가는 행렬 (n → m차원으로 가는 행렬)의 모델을 찾고 싶을 수 있음

이 때 행렬을 사용 → 행렬의 성질은 n by m이라고 했을 때, 이것의 transfer를 찾게 되면 n 차원에서 m 차원으로 가는 매핑을 정의하는 것

물론 변환 자체를 Affine Transfomation이라고 함

또한, 여기서는 w와 b가 행렬과 벡터이며 y는 $W^T$ 로 표현됨

이러한 행렬을 곱하는 것은 두 개의 벡터 스페이스의 변환이 좋은 해석

선형성을 가지는 변환이 있을 때, 그 변환은 항상 행렬로 표현

마찬가지로 행렬을 찾겠다는 것은 두 차원 간 선형변화를 찾겠다는 것과 같음

w와 b로 x라는 입력을 y라는 출력으로 보내겠다라고 해서 화살표로 함

3. Beyond Linear Neural Networks

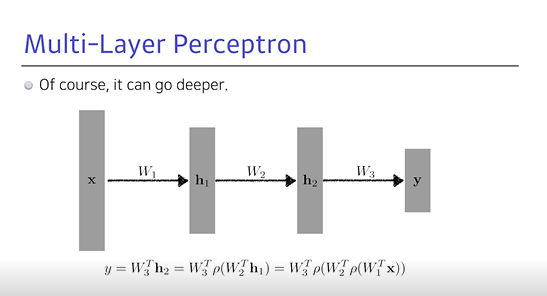
딥러닝은 NN를 깊게 쌓겠다는 것

이런 식으로 하나의 네트워크라고 하면 그렇게 나온 벡터를 $W_2$ 라는 것에 다시 곱할 수도 있음

이런 식으로 Deep하게 쌓을 수 있지만, 결국 행렬 두 개의 곱에 지나지 않기 때문에 1단짜리 NN에 지나지 않음

따라서 필요한 것은 중간인 nonlinear transform 필요

x라는 입력에서 y라는 출력으로 가는 이 맵핑이 표현할 수 있는 어떤 네트워크의 표현력을 최대한 극대화하기 위해서는 단순 선형결합을 n번 반복한는 것이 아님

한번 선형결합이 반복되면 그 뒤에 Activation function을 곱해서 nonlinear transform을 거치고, 그렇게 얻어지는 Feature를 다시 선형변환을 하고 (…) 이를 n번 반복하면 더 많은 표현력을 갖게 됨

이것이 바로 Neural Network

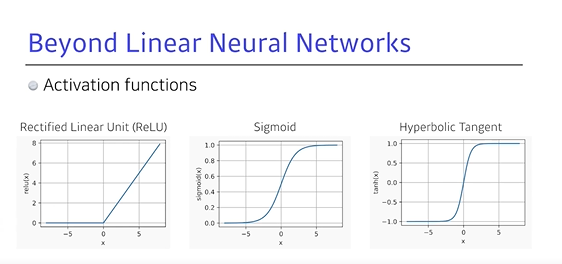
💡 어떤 activation function을 사용해야 할까?

ReLU : 어떤 아웃풋이 있으면, 0보다 큰 값은 그대로 쓰고 작은 값은 0으로 놓겠다는 변환

Sigmoid : 출력값을 항상 0~1사이로 제한

Hyperbolic Tangent : 출력값을 (-)(+)로 제한

어떤 것이 좋을지는 문제마다 다르며,
Activation function으로 nonlinear transform이 들어가야만 네트워크를 깊게 쌓았을 때 의미가 있음

hidden layer가 하나에 있는 NN는 어떤 continued한 measurable function (측정가능한 함수)을 근사할 수 있음

이는 단순 근사가 아닌 원하는 어떤 근삿값에 거의 맞출 수 있음

바꿔 말하면, hidden layer가 하나만 있는 NN의 표현력은 우리가 일반적으로 생각할 수 있는 어떤 continued한 function들을 다 포함해서 잘 됨

그러나, 사실은 이 표현은 존재성만을 보임. 즉, 이를 만족하는 NN가 세상 어디에 있다는 것이지 학습시키는 NN가 그럴 성질을 가질 것으로 보면 안 됨

4. Multi-Layer Perceptron

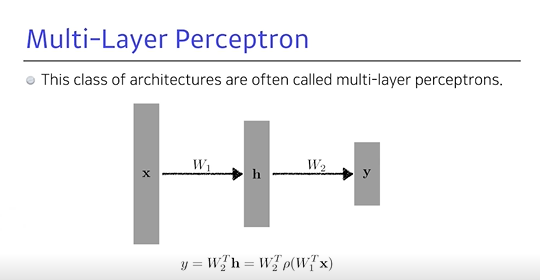
MLP라고 불리우는 구조, 입력이 주어져있고, 그 입력을 변화를 거쳐 나오는 hidden vector

hidden layer에서 다시 3단짜리 hidden layer가 있는 두 레이어를 보통 multy-layer perception 이라고 함

What about the loss functions?

Regression Task

Loss function에 대하여 입력이 주어졌을 때, 해당 출력값이 데이터셋에서 나오는 target 데이터 간의 제곱을 줄이는 것이 목적

그러나 이는 우리의 목적을 늘 만족하지는 않음, MSE가 0이 되면 출력값은 학습데이터의 target을 항상 맞추게 되는데 이는 늘 제곱일 필요가 없음

Loss function이 어떤 성질을 갖고 있고 이게 왜 원하는 결과를 얻어낼 수 있는 지를 이야기할 수 있어야 함

Classification Task

이 Loss function이 왜 분류문제를 잘 풀 수 있냐면, 일반적으로 분류문제의 아웃풋은 원화벡터로 표현함.
즉, 아웃풋이 찾고싶은 라벨이 10개면 10차원의 벡터가 나오게 됨

이 중에 생각하는 타겟이 만약 '강아지'면, 강아지에 해당하는 디멘젼이 2일 때 이것만 1이 되고 나머지는 다 0이 됨

$\hat y$ 은 로짓(?)이라고 보통 말 하는데, NN의 출력값 중에서 해당 클래스의 해당 값만 올리겠다는 것

그 차원에 해당하는 출력값을 키우는 것이 목적으로, 분류를 한다고 했을 때 D개의 라벨을 갖는 분류를 한다면, 아웃풋이 나왔을 때 d개의 아웃풋 중 제일 큰 숫자가 들어가 있는 인덱스만을 출력하게 됨

그 값은 중요하지 않고 다른 9개의 값에 비해 r번째의 y값이 높기만 하면 되고, 그렇게 되면 분류를 잘하게 됨

분류를 잘 하는 관점에서 다른 값 대비 높기만 하면 됨

Probabilistic Task

어떤 모델의 아웃풋이 단순히 숫자가 아니라 확률적인 모델을 하고 싶을 때

얼굴을 보고 나이를 맞추고 싶지만 애매할 때 활용