[모두를 위한 선형대수학] 3. 부분공간(subspace)과 부분공간의 기저

보충자료

벡터 공간 $V$의 공집합이 아닌 부분집합 $W$가 벡터공간 구조를 가질 때,
즉, 부분집합 $W$ → 벡터공간 $V$ 에서 정의된 덧셈 연산과 스칼라곱 연산을 만족할 때, 부분집합 $W$를 벡터 부분공간(vector subspace)이라고 함

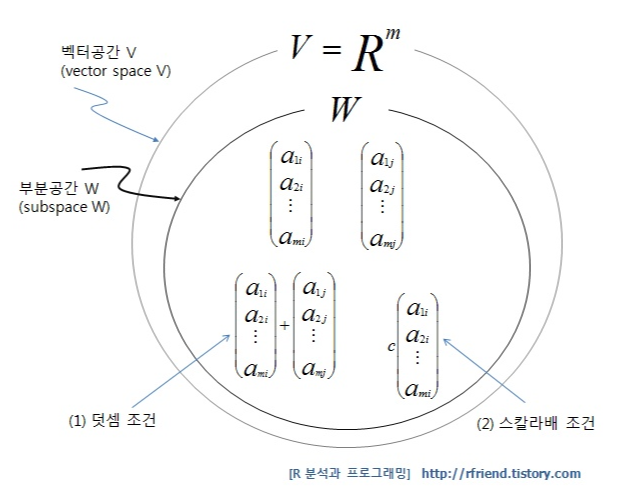
위에서 벡터공간(vector space) $V$의 부분집합 $W$가 위에서 설명한 (1) 덧셈 조건, (2) 스칼라배 조건을 모두 만족할 때,
$W$를 부분공간(subspace)을 벤다이어그램으로 나타내보면 아래와 같음.

부분공간은 '원점을 지나는 직선'이나 '원점을 지나는 평면' (zero vector를 포함)
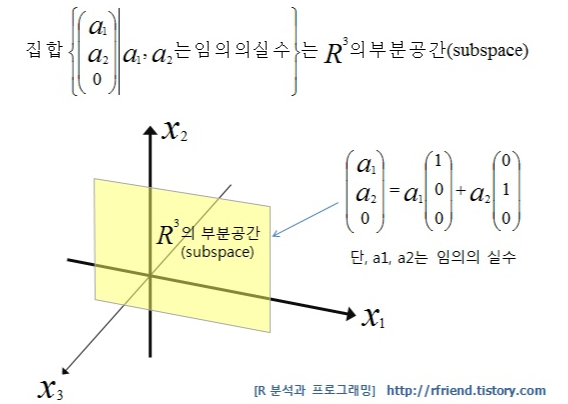
- 아래 예는 '원점을 지나는 평면'인 부분공간 예

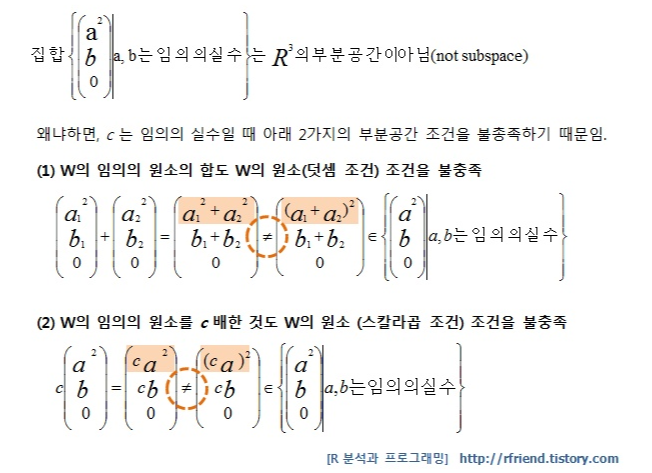
부분공간의 2가지 조건이었던 (1) 덧셈 조건, (2) 스칼라곱 조건을 만족하지 않으면 부분공간이라고 할 수 없음

생성공간(span), 생성된 부분공간(space spanned by) 성분의 수가 같은 벡터들
a(1), ..., a(n)이 주어졌다고 하고, 이들의 1차결합으로 표현되는 모든 벡터들의 집합을
이들 벡터들의 생성된 부분공간(space spanned by)

생성공간(span)은 그 자체로 벡터공간이 되며, 만일 주어진 벡터들 a(1), ..., a(n)이
선형독립 (1차 독립)이라면 이 벡터들은 해당 생성공간의 기저가 되며, a(1), ..., a(n) 벡터를 풀어서 설명해보면 아래와 같음

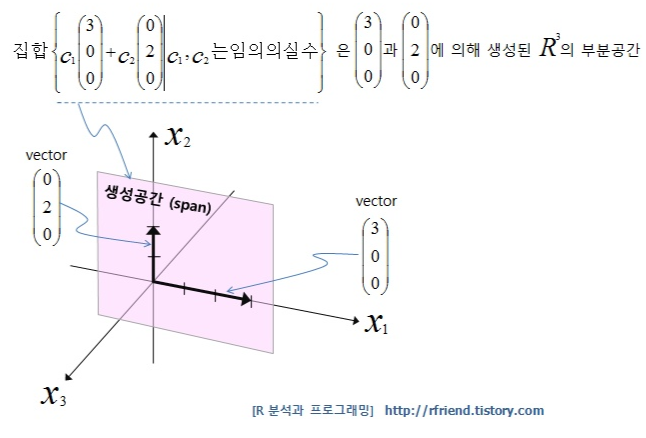
이걸 한번 더 풀어보면, 아래의x1x2 평면(plane)은 vector(3, 0, 0)과 vector(0, 2, 0)에 의해 생성된 R^3의 부분공간 (space spanned by (3,0,0), (0,2,0))
당연히 아래 생성공간은 벡터공간이며, vector(3,0,0)과 vector(0,2,0)은
선형독립(1차 독립)이므로 이 두 벡터의 집합은 벡터공간의 기저(base)

위의 예의 생성된 공간(span)은 기저의 원소(벡터)의 개수가 2개이므로
2차원(2 dimension)의 부분공간(subspace)

차원(dimension)벡터공간 V에 속한 1차독립 (선형독립) 벡터들의 최대 수를 V의 차원(dimension)이라 부르고, dim V로 표기,
(여기서 벡터공간의 차원은 유한(finite)하다고 가정)
W가 $R^m$의 부분공간이고, 벡터 a(1), a(2), ..., a(n) 이 W의 선형독립 원소라고 할 때,
기저의 원소 개수가 부분공간 W의 차원,이를 좀더 쉽게 풀어서 쓰면 아래와 같음

앞으로 선형사상을 공부하게 되면 n 차원의 상에 mn 행렬을 곱해서 m차원의 상으로 바꾸는게 나옵니다. 예를 들면, 2차원 영화를 3차원 3D영화로 바꾼다거나, 3차원 3D영화를 2차원 2D영화로 영상을 바꿀 때 선형대수가 쓰인답니다. 물리학자들이 말하는 초끈이론에서는 11차원속에서 진동하는 미세한 에너지끈을 연구를 한다는것을 들어보신분도 있을텐데요, 3차원까지는 우리가 상상을 해도 4차원 이상이 되면 '도대체 4차원, 5차원, 6차원....11차원이 뭐지?'라고 갸우뚱할 분이 많을 것 같습니다.이세돌과 대국을 펼쳤던 알파고는 "19 x 19 바둑판의 각 칸마다 48차원의 특징점들을 적용하여 총 19x19x48=17328차원의 거대한 벡터를 입력값으로 사용하였는데, 이는 마치 이미지와 같은 고차원의 상태공간으로 볼 수 있다"(핸드폰 메모장에 적어놨던건데요, 출처 기억 못함... -_-;)고 하는군요.암튼 수학자들이 정의하는 차원은 위와 같습니다.
m차원의 R^m 벡터공간의 부분집합 W의 원소가 n개 이면 W의 차원은 n차원이 된다. 헷갈리고 이해가 안된다면 위의 설명 한번 더 보시구요. ^^'R 의 matrix() 함수를 사용해서 mn 행렬(matrix)를 만드는 방법과, dim() 함수를 사용해서 차원(dimension)을 알아보는 방법은 아래와 같습니다.

A <- matrix(
+      c(1:12), # the data elements
+      nrow=3,              # number of rows
+      ncol=4,              # number of columns
+      byrow = TRUE)        # fill matrix by rows
A
     [,1] [,2] [,3] [,4]
[1,]    1    2    3    4
[2,]    5    6    7    8
[3,]    9   10   11   12
> dim(A)
[1] 3 4

1. 선형부분공간

• Subspace (부분공간) of $R^n → xi \in R 1 \leq i \leq n$
• $V \in$ subset(부분집합) of $R^n$
• $V$ subspace of $R^n$
• $V$ contains $0$

• 스칼라 곱셈에 닫혀있다.

  $\vec x$ in $V = \vec Cx$ in $V$

• 덧셈에 닫혀있다. (closure) ⇒ 'subspace'

  $\vec a$ in $V$ & $\vec b$ in $V$ → must $\vec a+\vec b$ in $V$

---

→ 부분집합의 원소 2개가 있다면, 두 원소를 더하면 이것은 부분집합 내의 임의의 두 원소가 된다.
→ 그리고 두 원소를 더하면 부분집합 내의 또 다른 원소를 얻는다.

$-1{a\brack b} = {-a\brack -b}$

---

→ 0이 아닌 원소에 음수를 곱하면 범위에서 벗어난다.
→ 위 $R^2$의 부분집합은 부분공간이 아니며, 곰셈 or 스칼라 곰셈에 닫혀있기 때문이다.

---

$U = span(\vec v1, \vec v_2, \vec v_3) =$ vaild subspace of $R^n$?

---

$\vec x =c_1\vec v_1 + c_2\vec v_2 + c_3\vec c_3$
$\vec a =ac_1\vec v_1 + ac_2\vec v_2 + ac_3\vec v_3$ → 곱셈에 닫혀있다.

---

→ 이것은 명백히 세 벡터들의 또 다른 선형결합
→ 선형생성은 세 벡터의 모든 선형결합들의 집합
→ 따라서, 이것은 그 선형결합들 중 하나이고, 따라서 이또한 선형생성 안에 포함
→ 즉, $V$에 포함 돼 있음

$\vec y = d_1\vec v_1 +d_2\vec v_2+d_3\vec v_3$
$\vec x +\vec y = (v_1+d_1)\vec v_1 +(v_2+d_2)\vec v_2+(v_3+d_3)\vec v_3$

---

→ 덧셈에 닫혀있음
→ 괄호 안은 단지 상수에 불과하기 때문에, $v_1, v_2, v_3$의 선형결합

$V$ span $({1\brack 1})$

---

→ 벡터 (1,1)의 생성은 이 벡터의 모든 선형결합

---

$V{1\brack 1} = {0\brack 0}$

---

→ 모든 실수 c에 대해 (1,1)을 곱하면, 그것이 span(생성)이 됨
→ 명백히 이것에 무엇을 곱해도 생성 안에 있는 것과 동일

---

$\vec a = {1\brack 1}, \vec b = {1\brack 1}$ ⇒ $C_1{1\brack 1} + C_2{1\brack 1} =(C_1+C_2){1\brack 1}$

---

→ 곱셈과 덧셈에 대해 닫혀있으며 영벡터도 포함하고 있다.
→ 생성(span)이 유효한 부분공간(subspace)

2. 부분공간의 기저

subspace $V = span(\vec v_1,\vec v_2 ...\vec v_n)$
→ $v$들은 선형독립
→ span 생성은 이 부분공간이 여기의 벡터들로 만들 수 있는 모든 가능한 선형결합의 집합

---

$c_1\vec v_1+ ...c_n\vec v_n$
→ c는 모든 가능한 실수
→ 이 결합의 모든 경우의 수를 벡터의 집합으로 만들면, 그것이 span이며 부분공간 V의 정의
→ 선형독립의 정의는 곧 유일한 해가 0벡터라는 것이며 모든 항이 0

---

$S={\vec V_1,...,\vec V_n}$
→ S is a basis for V (벡터집합 S가 부분공간 v의 기저)
→ 이 벡터들이 부분공간을 생성하고, 부분공간의 어떠한 벡터로 될 수 있으며 그 벡터들은 선형독립이라는 것

만약 ${1\brack 0}$이 추가되면 선형종속이 되며, S는 $R^2$의 기저가 아니다.
즉, 기저집합이 되려면 최소한의 벡터들의 집합으로 이루어져야 한다.

3강. 요약정리