A* 알고리즘 in Python

Sia Lim·2024년 11월 12일

Path Searching for Game

목록 보기

4/10

A* 알고리즘 (A star 알고리즘)은 Dijkstra와 유사하지만, 추가적인 휴리스틱 함수(heuristic function)을 사용하여 목표 노드까지의 예상 거리를 고려함으로써 더 효율적으로 최단 경로를 찾는 알고리즘이다. 휴리스틱은 경로를 찾는 데 있어서 탐색 속도를 높여주며, 주로 맨해튼 거리 또는 유클리드 거리를 사용한다.

A* 알고리즘의 개념

A* 알고리즘은 각 노드에 대해 $f(n) = g(n) + h(n)$ 이라는 평가 함수를 사용한다.

$g(n)$ : 시작 노드에서 현재 노드 $n$ 까지의 실제 거리
$h(n)$ : 현재 노드 $n$ 에서 목표 노드까지의 예상 거리(휴리스틱)

이 두 값을 합한 $f(n)$ 값이 작은 노드부터 탐색해 나가므로 목표 지점까지 빠르게 도달할 수 있다.

Dijkstra 알고리즘과의 차이

	Dijkstra 알고리즘	*A 알고리즘**
목표 지향성	목표 지점 고려 없이 모든 방향 탐색	목표 방향으로의 예상 거리(휴리스틱)를 활용
평가 함수	f(n) = g(n)	f(n) = g(n) + h(n)
탐색 범위	모든 노드에 대한 최단 경로 탐색	목표 방향으로 탐색 범위를 좁힘
사용 사례	모든 노드의 최단 거리 필요 시	특정 목표까지의 최단 경로가 필요할 때
휴리스틱 사용	없음	있음 (예: 맨해튼 거리, 유클리드 거리 등)

Dijkstra 알고리즘

기본 원리 : 시작 노드에서 다른 모든 노드까지의 최단 거리를 찾는 알고리즘이다. 이때, 가중치를 기반으로 거리를 계산한다.
탐색 방식 : Dijkstra 알고리즘은 각 노드의 최단 거리만을 고려한다. 목표 노드의 위치 정보는 활용하지 않는다. 따라서 모든 경로를 최소 거리 기준으로 확정해 나가는 방식으로 동작한다.
적용 : 목표 지점이 정해져 있지 않거나, 모든 노드에 대해 최단 거리를 구할 때 적합하다.
시간 복잡도 : 일반적으로 Dijkstra는 $O((V+E) log V)$ 의 시간 복잡도를 가진다. ( $V$ : 노드 수, $E$ : 간선 수)

A* 알고리즘

기본 원리 : 시작 노드에서 "목표 노드"까지의 최단 경로 찾기
탐색 방식 : 가중치에 기반한 실제 거리 $g(n)$ 과 목표 지점까지의 예상 거리(휴리스틱) $h(n)$ 을 함께 사용한다. $f(n) = g(n) + h(n)$ 이라는 평가함수를 정의하여, 목표 지점까지의 예상 거리를 고려해서 탐색 범위를 좁힌다.
휴리스틱 함수 : $h(n)$ 함수는 현재 노드에서 목표 노드까지의 직선 거리, 맨해튼 거리, 유클리드 거리 등을 활용하여 목표까지의 거리 예측치를 제공한다. 따라서 목표 방향으로의 탐색 속도를 가속할 수 있다!
적용 : 목표 노드가 명확하게 정해진 경우에 적합하다. 지도 내 경로 탐색이나 게임 AI의 길찾기 등에 자주 사용된다.
시간 복잡도 : A* 알고리즘의 시간 복잡도는 휴리스틱에 따라 달라지지만, Dijkstra보다 적은 탐색으로 목표에 도달할 수 있어서, 실제 성능 면에서 더 효율적이다.

Python으로 A* 알고리즘 구현하기

전체 코드

import heapq
import math

# 휴리스틱 함수 : 유클리드 거리 계산 (노드 간의 직선 거리)
def heuristic(node1, node2):
    x1, y1 = node1
    x2, y2 = node2
    return math.sqrt((x1 - x2) **2 + (y1 - y2) **2)

def a_star(graph, start, goal):
    # 각 노드까지의 실제 거리 저장할 딕셔너리 (초기값 : 무한대)
    g_costs = {node: float('inf') for node in graph}
    g_costs[start] = 0

    # 우선순위 큐 초기화
    priority_queue = [(0, start)] # (f(n), node)
    came_from = {} # 경로 추적을 위한 딕셔너리

    while priority_queue:
        # 현재 노드를 큐에서 꺼냄
        current_f_cost, current_node = heapq.heappop(priority_queue)

        # 목표 노드에 도달한 경우 경로를 반환
        if current_node == goal:
            path = []
            total_cost = g_costs[goal]
            while current_node in came_from:
                path.append(current_node)
                current_node = came_from[current_node]
            path.append(start)
            return path[::-1], total_cost # 경로를 시작부터 끝까지로 반환
        
        # 인접 노드를 탐색
        for neighbor, cost in graph[current_node]:
            tentative_g_cost = g_costs[current_node] + cost
            if tentative_g_cost < g_costs[neighbor]:
                # 새로운 최단 거리 발견
                g_costs[neighbor] = tentative_g_cost
                f_cost = tentative_g_cost + heuristic(neighbor, goal)
                heapq.heappush(priority_queue, (f_cost, neighbor))
                came_from[neighbor] = current_node

    return None, None # 경로가 없는 경우

# 그래프 정의 (인접 리스트)
# 노드 위치가 좌표 (x, y)로 정의됨
graph = {
    (0, 0): [((2, 0), 3), ((0, 2), 2)],
    (2, 0): [((0, 0), 3), ((2, 2), 5), ((4, 0), 2)],
    (0, 2): [((0, 0), 2), ((2, 2), 4)],
    (2, 2): [((2, 0), 5), ((0, 2), 4), ((4, 2), 3)],
    (4, 0): [((2, 0), 2), ((4, 2), 1)],
    (4, 2): [((2, 2), 3), ((4, 0), 1), ((4, 4), 2)],
    (4, 4): [((4, 2), 2)]
}

start = (0, 0)
goal = (4, 4)
path, total_cost = a_star(graph, start, goal)

print("최단 경로 : ", path)
print("가중치 합 : ", total_cost)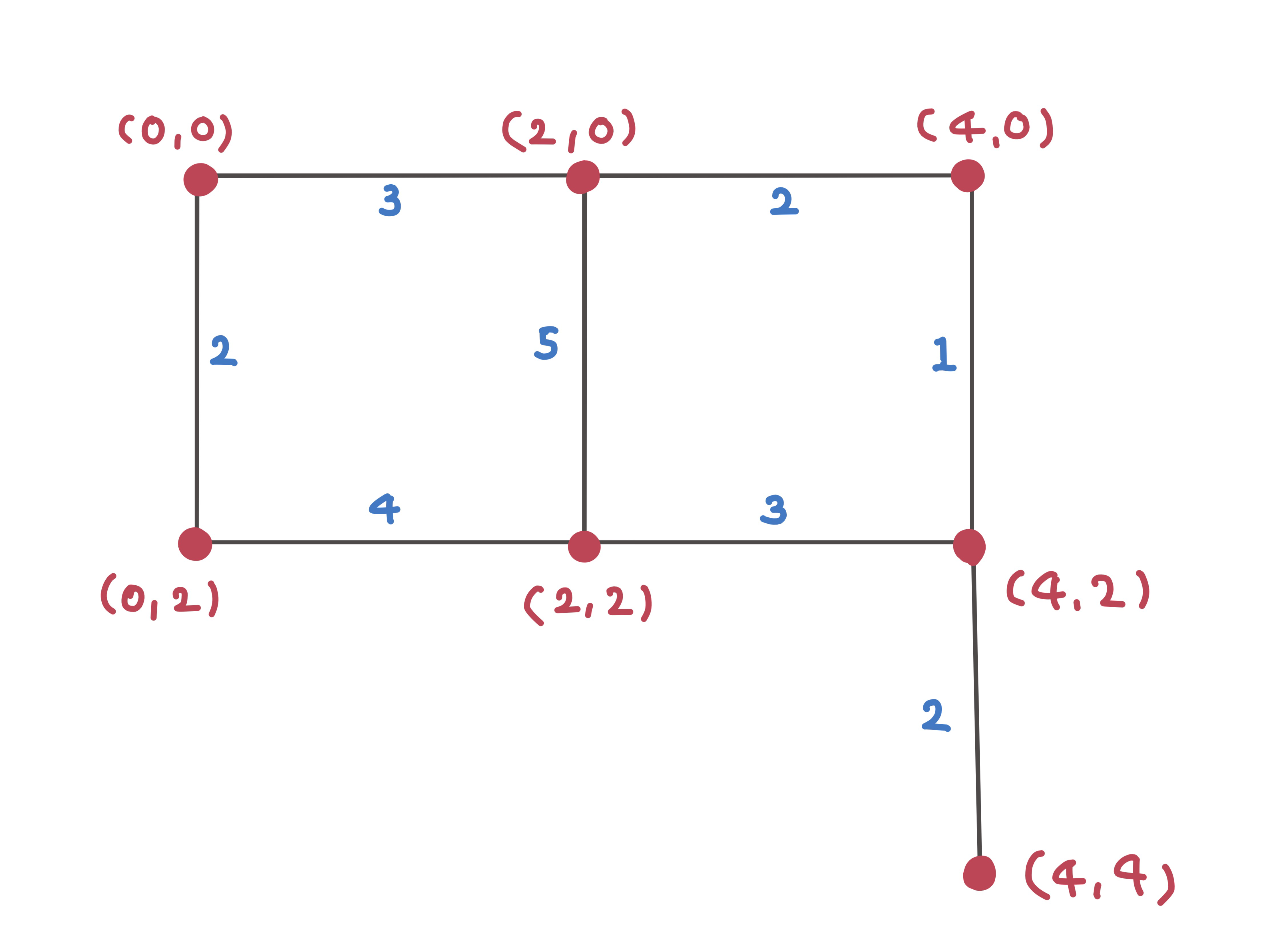

대략적인 그래프의 형태는 위 그림과 같다.

코드 상세 구조

1. `heuristic` 함수

# 휴리스틱 함수 : 유클리드 거리 계산 (노드 간의 직선 거리)
def heuristic(node1, node2):
    x1, y1 = node1
    x2, y2 = node2
    return math.sqrt((x1 - x2) **2 + (y1 - y2) **2)

유클리드 거리를 사용해서 두 노드 간의 직선 거리를 계산한다.
node1과 node2의 좌표 $(x_1, y_1)$ 와 $(x_2, y_2)$ 가 주어지면, 두 좌표 사이의 직선거리를 구한다.

2. `a_star` 함수 초기화

A* 알고리즘의 메인 함수인 a_star는 시작점에서 목표 지점까지의 최단 경로를 찾는다.

def a_star(graph, start, goal):
    # 각 노드까지의 실제 거리 저장할 딕셔너리 (초기값 : 무한대)
    g_costs = {node: float('inf') for node in graph}
    g_costs[start] = 0

    # 우선순위 큐 초기화
    priority_queue = [(0, start)] # (f(n), node)
    came_from = {} # 경로 추적을 위한 딕셔너리

g_costs : 시작 노드에서 각 노드까지의 실제 거리를 저장한다. 초기에는 무한대로 설정하고, 시작 노드에서 시작 노드까지의 거리는 0으로 설정한다.
- 이때 Dijkstra에서와 같이 distance가 아닌 cost라고 한 것은 아래에 추가적으로 설명하겠다.
priority_queue : (f(n), node) 형태로 우선순위 큐를 초기화한다. 이때 $f(n) = g(n) + h(n)$ 은 A* 알고리즘의 평가함수.
- $g(n)$ : 시작 노드에서 현재 노드 $n$ 까지의 실제 거리
- $h(n)$ : 현재 노드 $n$ 에서 목표 노드까지의 예상 거리(휴리스틱)
came_from : 각 노드의 이전 노드를 저장하여 경로를 추적할 때 사용한다

3. 메인 탐색 루프

priority_queue에서 가장 우선순위가 높은(최단 거리 예상) 노드를 하나씩 꺼내서 탐색을 진행한다.

    while priority_queue:
        # 현재 노드를 큐에서 꺼냄
        current_f_cost, current_node = heapq.heappop(priority_queue)

        # 목표 노드에 도달한 경우 경로를 반환
        if current_node == goal:
            path = []
            total_cost = g_costs[goal]
            while current_node in came_from:
                path.append(current_node)
                current_node = came_from[current_node]
            path.append(start)
            return path[::-1], total_cost # 경로를 시작부터 끝까지로 반환

heapq.heappop(priority_queue) : priority_queue에서 현재까지 발견된 최단 예상 거리의 노드를 꺼낸다.
- Python의 heapq 모듈은 리스트를 최소 힙(min heap)으로 사용하도록 되어 있다. heapq.heappop()를 사용하면 가장 작은 값을 가진 요소를 큐에서 제거하면서 반환한다.
- A* 알고리즘에서 요소를 제거하는 이유 : 이미 최단 경로가 확정된 노드를 다시 탐색할 필요가 없기 때문. 큐에서 꺼낸 요소는 이미 탐색이 완료된 노드로 간주할 수 있다.
목표 노드 도달 확인 : 꺼낸 노드가 목표 노드라면 경로 추적을 시작한다.
- came_from 딕셔너리를 사용하여 goal에서 시작 노드까지의 경로를 역순으로 찾고, 최종적으로 뒤집어서 반환한다.

4. 인접 노드 탐색 및 거리 계산

현재 노드의 인접 노드를 탐색하며, 각각의 $f(n)$ 값을 업데이트한다.

        # 인접 노드를 탐색
        for neighbor, cost in graph[current_node]:
            tentative_g_cost = g_costs[current_node] + cost
            if tentative_g_cost < g_costs[neighbor]:
                # 새로운 최단 거리 발견
                g_costs[neighbor] = tentative_g_cost
                f_cost = tentative_g_cost + heuristic(neighbor, goal)
                heapq.heappush(priority_queue, (f_cost, neighbor))
                came_from[neighbor] = current_node

tentative_g_cost : 현재 노드에서 인접 노드까지의 임시 실제 거리를 계산한다. (tentative : 잠정적인)
- tentative_g_cost = g_costs[current_node] + cost는 현재 노드까지의 거리 g_costs[current_node]와 인접 노드까지의 비용 cost의 합이다.
조건문 : tentative_g_cost가 기존의 g_costs[neighbor]보다 작다면 새로운 최단거리가 발견된 것이다.
- g_costs[neighbor]를 갱신하고, f_cost = tentative_g_cost + heuristic(neighbor, goal)를 통해 $f(n)$ 을 계산한다.
- 새로운 (f_cost, neighbor)를 우선순위 큐에 추가한다.
- came_from[neighbor] = current_node로 경로를 추적할 수 있도록 came_from 딕셔너리를 업데이트한다.

5. 반환값

경로가 발견되면 경로 리스트와 가중치 합을 반환한다. 목표에 도달할 수 없으면 None, None 을 반환한다.

실행 결과

최단 경로 :  [(0, 0), (2, 0), (4, 0), (4, 2), (4, 4)]
가중치 합 :  8

현재 그래프를 보면, $(0, 0)$ 에서 $(4, 4)$ 까지의 최단 경로로 다음과 같은 예를 들 수 있다.

$(0, 0)\rightarrow(0, 2)\rightarrow(2, 2)\rightarrow(4,2)\rightarrow(4, 4)$
- 가중치 합 : $2+4+3+2=11$
$(0, 0)\rightarrow(2,0)\rightarrow(4, 0)\rightarrow(4,2)\rightarrow(4, 4)$
- 가중치 합 : $3+2+1+2=8$

이때 A* 알고리즘이 선택한 경로는 2번 경로인 $(0, 0)\rightarrow(2,0)\rightarrow(4, 0)\rightarrow(4,2)\rightarrow(4, 4)$ 이고, 가중치 합은 8이다. 가중치가 가장 작기 때문에 최단 경로로 선택되었다.

`distance`가 아닌 `cost`가 된 이유

`cost`와 `distance`의 차이

distance : 보통 물리적 거리를 의미한다. Dijkstra 알고리즘에서는 노드 간의 거리(혹은 가중치)가 최단 경로 계산의 기준이기 때문에 distance라는 용어가 적합하다.
cost: 단순한 물리적 거리뿐만 아니라 다양한 의미의 비용을 포함할 수 있다. A* 에서는 거리뿐만 아니라 목표 노드까지의 예상 비용( $h(n)$ )을 포함해 경로를 평가하므로, 비용의 개념이 더 일반적이고 적합하다.

A* 에서 `cost` 사용의 의미

A 알고리즘에서 cost라는 용어를 사용하면 단순 거리 이상의 다양한 비용을 포괄할 수 있다. 예를 들어, 게임에서 A 알고리즘을 사용할 때 이동 비용이 단순한 거리뿐만 아니라 지형의 난이도, 장애물 회피 비용 등을 포함할 수도 있기 때문에 cost라는 용어가 더 일반적이라고 볼 수 있다.

따라서 위에서 Python으로 작성한 A* 알고리즘에서는 g_costs라는 이름을 사용해 누적 비용을 나타냈다.