A* 알고리즘 in C++

Sia Lim·2024년 11월 13일

Path Searching for Game

목록 보기

5/10

파이썬으로 구현한 A* 알고리즘은 아래 링크에서...

A* 알고리즘 (A star 알고리즘)은 Dijkstra와 유사하지만, 추가적인 휴리스틱 함수(heuristic function)을 사용하여 목표 노드까지의 예상 거리를 고려함으로써 더 효율적으로 최단 경로를 찾는 알고리즘이다. 휴리스틱은 경로를 찾는 데 있어서 탐색 속도를 높여주며, 주로 맨해튼 거리 또는 유클리드 거리를 사용한다.

A* 알고리즘의 개념

A* 알고리즘은 각 노드에 대해 $f(n) = g(n) + h(n)$ 이라는 평가 함수를 사용한다.

$g(n)$ : 시작 노드에서 현재 노드 $n$ 까지의 실제 거리
$h(n)$ : 현재 노드 $n$ 에서 목표 노드까지의 예상 거리(휴리스틱)

이 두 값을 합한 $f(n)$ 값이 작은 노드부터 탐색해 나가므로 목표 지점까지 빠르게 도달할 수 있다.

C++로 A* 알고리즘 구현하기

전체 코드

C++ 왜이렇게 어렵냐!!!?

#include <iostream>
#include <vector>
#include <queue>
#include <unordered_map>
#include <cmath>
#include <utility>
#include <limits>

using namespace std;

// 해시 함수 정의
struct hash_pair {
    template <class T1, class T2>
    size_t operator()(const pair<T1, T2>& p) const {
        auto hash1 = hash<T1>{}(p.first);
        auto hash2 = hash<T2>{}(p.second);
        return hash1 ^ (hash2 << 1);
    }
};

// 두 좌표 사이의 유클리드 거리 (휴리스틱)
double heuristic(pair<int, int> node1, pair<int, int> node2) {
    int x1 = node1.first, y1 = node1.second;
    int x2 = node2.first, y2 = node2.second;
    return sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 -  y2));
}

// A* 알고리즘
pair<vector<pair<int, int>>, double> a_star(
    const unordered_map<pair<int, int>, vector<pair<pair<int, int>, int>>, hash_pair>& graph,
    pair<int, int> start, pair<int, int> goal) {
        unordered_map<pair<int, int>, double, hash_pair> g_costs;
        unordered_map<pair<int, int>, pair<int, int>, hash_pair> came_from;

        for (const auto& node : graph) {
            g_costs[node.first] = numeric_limits<double>::infinity();
        }
        g_costs[start] = 0;

    // 우선순위 큐 선언
    priority_queue<pair<double, pair<int, int>>, vector<pair<double, pair<int, int>>>, greater<pair<double, pair<int, int>>>> pq;
    pq.push({0, start});

    while (!pq.empty()) {
        auto [current_f_cost, current_node] = pq.top();
        pq.pop();

        if (current_node == goal) {
            vector<pair<int, int>> path;
            double total_cost = g_costs[goal]; // 최단 경로의 총 가중치
            while (came_from.find(current_node) != came_from.end()) {
                path.push_back(current_node);
                current_node = came_from[current_node];
            }
            path.push_back(start);
            reverse(path.begin(), path.end());
            return {path, total_cost};
        }

        for (const auto& [neighbor, cost] : graph.at(current_node)) {
            double tentative_g_cost = g_costs[current_node] + cost;
            if (tentative_g_cost < g_costs[neighbor]) {
                g_costs[neighbor] = tentative_g_cost;
                double f_cost = tentative_g_cost + heuristic(neighbor, goal);
                pq.push({f_cost, neighbor});
                came_from[neighbor] = current_node;
            }
        }
    }
    return {{}, numeric_limits<double>::infinity()}; // 경로가 없는 경우
}

int main() {
    // 그래프 정의
    unordered_map<pair<int, int>, vector<pair<pair<int, int>, int>>, hash_pair> graph;
    graph[{0, 0}] = {{{2, 0}, 3}, {{0, 2}, 2}};
    graph[{2, 0}] = {{{0, 0}, 3}, {{2, 2}, 5}, {{4, 0}, 2}};
    graph[{0, 2}] = {{{0, 0}, 2}, {{2, 2}, 4}};
    graph[{2, 2}] = {{{2, 0}, 5}, {{0, 2}, 4}, {{4, 2}, 3}};
    graph[{4, 0}] = {{{2, 0}, 2}, {{4, 2}, 1}};
    graph[{4, 2}] = {{{2, 2}, 3}, {{4, 0}, 1}, {{4, 4}, 2}};
    graph[{4, 4}] = {{{4, 2}, 2}};

    pair<int, int> start = {0, 0};
    pair<int, int> goal = {4, 4};
    auto [path, total_cost] = a_star(graph, start, goal);

    cout << "최단 경로 : \n";
    for (const auto& node : path) {
        cout << "(" << node.first << "," << node.second << ") ";
    }
    cout << "\n총 가중치 합 : " << total_cost << endl;

    return 0;
}

코드 상세 구조

대략적 코드 구조 개괄

해시 함수 구조체 정의
휴리스틱 함수 정의
A* 알고리즘 함수 정의
메인 함수와 그래프 정의

1. 해시 함수 구조체 정의

// 해시 함수 정의
struct hash_pair {
    template <class T1, class T2>
    size_t operator()(const pair<T1, T2>& p) const {
        auto hash1 = hash<T1>{}(p.first);
        auto hash2 = hash<T2>{}(p.second);
        return hash1 ^ (hash2 << 1);
    }
};

해시 함수 구조체 : unordered_map 에서 pair<int, int> 타입을 키로 사용하기 위해 필요
C++에서 기본적으로 제공되는 unordered_map은 int, string 같은 단순한 자료형을 키로 사용할 때는 해시를 자동으로 처리함. 하지만 pair<int, int> 처럼 복잡한 타입은 기본적으로 해시를 지원해주지 않기 때문에 해시 함수를 만들 필요가 있었음.

코드 각 줄의 의미

struct hash_pair { ... };
- hash_pair 라는 이름의 구조체를 정의함. 이 구조체의 역할은 사용자 정의 해시 함수를 제공하기 위함임.
template <class T1, class T2>
- pair<T1, T2>는 두 개의 타입 T1과 T2로 이루어진 쌍이기 때문에, 이 구조체가 다양한 타입의 pair에도 적용될 수 있도록 T1과 T2를 일반화(template)함.
- 이 template으로 인해 pair<int, int>, pair<string, int>, pair<double, string>등 다양한 pair타입도 해시를 생성할 수 있음.
- 물론 이 코드에서 일반화(template)를 꼭 사용할 필요는 없었음. 그렇게 하지 않고 pair<int, int>에만 적용되도록 작성했어도 코드는 작동했을 것.
- 하지만 모름지기 개발자라면... 재사용성을 습관적으로 생각하게 되기 때문에...
size_t operator() const pair<T1, T2>& p) const { ... }
- 이 부분은 해시 함수를 정의하는 연산자 오버로딩이다.
- operator()는 함수처럼 호출되는 특별한 연산자로, unordered_map이 해시 값을 필요로 할 때마다 이 연산자가 호출된다.
- 이 함수는 pair의 해시 값을 계산하고, unordered_map에서 키로 사용할 수 있는 size_t타입의 값을 반환한다.
auto hash1 = hash<T1>{}(p.first);
- hash<T1>{}은 T1 타입의 값을 해시로 변환하는 C++ STL 기능이다.
return hash1 ^ (hash2 << 1);
- 두 개의 해시값을 결합하여 하나의 해시값을 만든다.
- hash2 << 1은 hash2를 왼쪽으로 한 비트 이동시킨다. (hash1과 hash2가 겹치지 않도록 비트 위치를 분산시킨다)
- ^는 XOR 연산자로, 두 해시값을 결합한다. 두 값의 비트가 다를 때 1을 생성해서, 해시 값을 유일하게 만드는 데 도움이 된다(완벽히 유일한 건 아니지만, 해시 충돌 가능성을 줄일 수 있음)
- 이 연산을 통해 pair 전체에 대해 고유한 해시값을 생성하여 반환한다.

2. 휴리스틱 함수 정의

// 두 좌표 사이의 유클리드 거리 (휴리스틱)
double heuristic(pair<int, int> node1, pair<int, int> node2) {
    int x1 = node1.first, y1 = node1.second;
    int x2 = node2.first, y2 = node2.second;
    return sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 -  y2));
}

3. A* 알고리즘 함수 정의

// A* 알고리즘
pair<vector<pair<int, int>>, double> a_star(
    const unordered_map<pair<int, int>, vector<pair<pair<int, int>, int>>, hash_pair>& graph,
    pair<int, int> start, pair<int, int> goal) {

반환 타입 : pair<vector<pair<int, int>>, double> 으로 최단 경로와 총 가중치를 반환한다. 최단 경로를 vector로 저장하는 것은, 경로상의 각 노드 pair<int, int>들을 순서대로 저장할 수 있기 때문.
unordered_map<pair<int, int>, vector<pair<pair<int, int>, int>>, hash_pair>& graph
- 그래프 : unordered_map을 사용하여 노드마다 연결된 인접 노드와 가중치 저장
- pair<int, int> : 노드의 좌표
- vector<pair<pair<int, int>, int>> : 인접 노드의 좌표와 그 간선의 가중치
const의 의미 : 상수성
- 함수 매개변수 앞에 const를 붙이면 함수 내부에서 해당 매개변수를 변경할 수 없음을 의미 (즉, 읽기 전용)
- const를 사용함으로써 함수 내에서 graph가 수정되는 실수를 방지
&의 의미 : 참조자
- 함수 매개변수에서 &를 사용하면, 해당 매개변수를 참조로 전달(pass by reference)하게 됨. 즉, 객체의 복사본을 생성하지 않고 원래 객체를 참조하여 사용함.
- unordered_map과 같이 큰 객체를 값으로 전달하면 객체의 복사본이 생성되며, 메모리와 시간을 많이 소모하게 됨. &를 사용하면 복사 없이 원본 객체를 참조하므로 성능이 향상되고 메모리 사용량을 절약할 수 있음.
- pass by value vs pass by reference (아 이제 기억났다!)

        unordered_map<pair<int, int>, double, hash_pair> g_costs;
        unordered_map<pair<int, int>, pair<int, int>, hash_pair> came_from;

g_costs : 각 노드의 누적 거리( $g(n)$ )를 저장
came_from : 경로 추적을 위해 현재 노드에 도달한 직전 노드를 저장할 곳

        for (const auto& node : graph) {
            g_costs[node.first] = numeric_limits<double>::infinity();
        }
        g_costs[start] = 0;

모든 노드의 초기 거리를 infinity로 설정하고 시작 노드의 거리는 0으로 초기화한다.

    // 우선순위 큐 선언
    priority_queue<pair<double, pair<int, int>>, vector<pair<double, pair<int, int>>>, greater<pair<double, pair<int, int>>>> pq;
    pq.push({0, start});

priority_queue : C++의 우선순위 큐. greater<...>를 사용해 최소 힙으로 만들어, $f(n)$ 의 값이 가장 작은 노드가 먼저 나오도록 설정한다.
- C++의 priority_queue는 세 가지 템플릿 인자를 받는다.
```
priority_queue<요소의 타입, 내부 컨테이너, 비교 함수>
```
pair<double, pair<int, int>> : priority_queue에 저장할 요소의 타입. $f(n)$ 값을 기준으로 정렬하기 위해 pair<double, pair<int, int>>를 사용하고, double 타입의 $f(n)$ 값이 첫번째 요소로 들어감.
vector<pair<double, pair<int, int>>> : priority_queue의 내부 컨테이너로, 데이터를 저장하기 위한 기본 자료구조
- 왜 vector가 내부 컨테이너로 지정되는가? : priority_queue는 내부적으로 데이터를 정렬된 상태로 유지해야 함. 이때 vector를 내부 자료구조로 사용하면 데이터를 연속적인 메모리 공간에 저장하면서 효율적으로 관리할 수 있다. vector는 priority_queue에서 데이터를 추가하거나 제거할 때 힙 연산을 수행하기에 적합한 자료구조!!!
greater<pair<double, pair<int, int>>> : 우선순위를 결정하는 비교 함수. $f(n)$ 의 값이 작은 순서대로 pair를 정렬한다.
pq.push({0, start}); : 시작 노드를 $f(n) = 0$ 값으로 큐에 추가한다.

4. 메인 탐색 루프

    while (!pq.empty()) {
        auto [current_f_cost, current_node] = pq.top();
        pq.pop();

탐색 루프 : 우선순위 큐가 빌 때까지 반복해서 최단 경로를 탐색한다.
auto : C++의 자동 타입 추론. 변수의 타입을 명시적으로 적지 않아도, 컴파일러가 우변의 타입을 기준으로 변수의 타입을 자동 추론한다.
- 복잡한 타입에 대해서 자동으로 추론하므로 코드를 짧고 가독성이 좋게 만든다. 만약 데이터 타입이 변경되더라도 수정할 필요가 없어서 유지보수에 좋다.
[current_f_cost, current_node] : 구조적 바인딩. pq.top()이 반환하는 pair<double, <pair<int, int>> 타입의 값을 구조적 바인딩으로 분리하여, current_f_cost와 current_node라는 개별 변수로 할당할 수 있다.

        if (current_node == goal) {
            vector<pair<int, int>> path;
            double total_cost = g_costs[goal]; // 최단 경로의 총 가중치
            while (came_from.find(current_node) != came_from.end()) {
                path.push_back(current_node);
                current_node = came_from[current_node];
            }
            path.push_back(start);
            reverse(path.begin(), path.end());
            return {path, total_cost};
        }

목표 노드 도달 확인 : current_node가 goal 이면 경로 추적을 시작한다.
경로 추적 : came_from 맵을 이용해 목표에서 시작까지 경로를 역순으로 추적한 후, reverse()로 뒤집어 반환한다.

5. 인접 노드 탐색 및 거리 갱신

        for (const auto& [neighbor, cost] : graph.at(current_node)) {
            double tentative_g_cost = g_costs[current_node] + cost;
            if (tentative_g_cost < g_costs[neighbor]) {
                g_costs[neighbor] = tentative_g_cost;
                double f_cost = tentative_g_cost + heuristic(neighbor, goal);
                pq.push({f_cost, neighbor});
                came_from[neighbor] = current_node;
            }
        }

인접 노드 탐색 : 현재 노드의 인접 노드와 가중치를 순회한다.
tentative_g_cost : 현재 노드를 통해 인접 노드에 도달하는 누적 거리를 계산한다.
최단 거리 갱신이 필요한 경우, g_costs, f_cost, 그리고 came_from을 갱신한다.

    return {{}, numeric_limits<double>::infinity()}; // 경로가 없는 경우
}

어제 Python으로 A* 알고리즘 구현했을 때는 경로가 없는 경우에 대해서 return None, None을 사용할 수 있었다. Python에는 None이라는, 비어 있음을 명확히 표현하는 객체가 있기 때문에 가능했다. 아주 직관적이고 좋지 않은가?

하지만 C++에서는 None에 해당하는 객체가 없다. 또, 반환 타입이 pair<vector<pair<int, int>>, double>로 고정되어 있기 때문에 None 같은 특수 값을 사용할 수 없다. 그래서 이번 C++에서의 구현은 빈 벡터와 무한대 값을 반환하여 경로가 없음을 표현하도록 작성했다.

6. 메인 함수와 그래프 정의

int main() {
    // 그래프 정의
    unordered_map<pair<int, int>, vector<pair<pair<int, int>, int>>, hash_pair> graph;
    graph[{0, 0}] = {{{2, 0}, 3}, {{0, 2}, 2}};
    graph[{2, 0}] = {{{0, 0}, 3}, {{2, 2}, 5}, {{4, 0}, 2}};
    graph[{0, 2}] = {{{0, 0}, 2}, {{2, 2}, 4}};
    graph[{2, 2}] = {{{2, 0}, 5}, {{0, 2}, 4}, {{4, 2}, 3}};
    graph[{4, 0}] = {{{2, 0}, 2}, {{4, 2}, 1}};
    graph[{4, 2}] = {{{2, 2}, 3}, {{4, 0}, 1}, {{4, 4}, 2}};
    graph[{4, 4}] = {{{4, 2}, 2}};

    pair<int, int> start = {0, 0};
    pair<int, int> goal = {4, 4};
    auto [path, total_cost] = a_star(graph, start, goal);

    cout << "최단 경로 : \n";
    for (const auto& node : path) {
        cout << "(" << node.first << "," << node.second << ") ";
    }
    cout << "\n총 가중치 합 : " << total_cost << endl;

    return 0;
}

그래프 정의 : 각 노드와 인접 노드 및 가중치를 unordered_map을 사용해 정의한다.
a_star 함수 호출 : 시작점과 목표점을 입력으로 최단 경로와 총 가중치를 반환받아 출력한다.

실행 결과

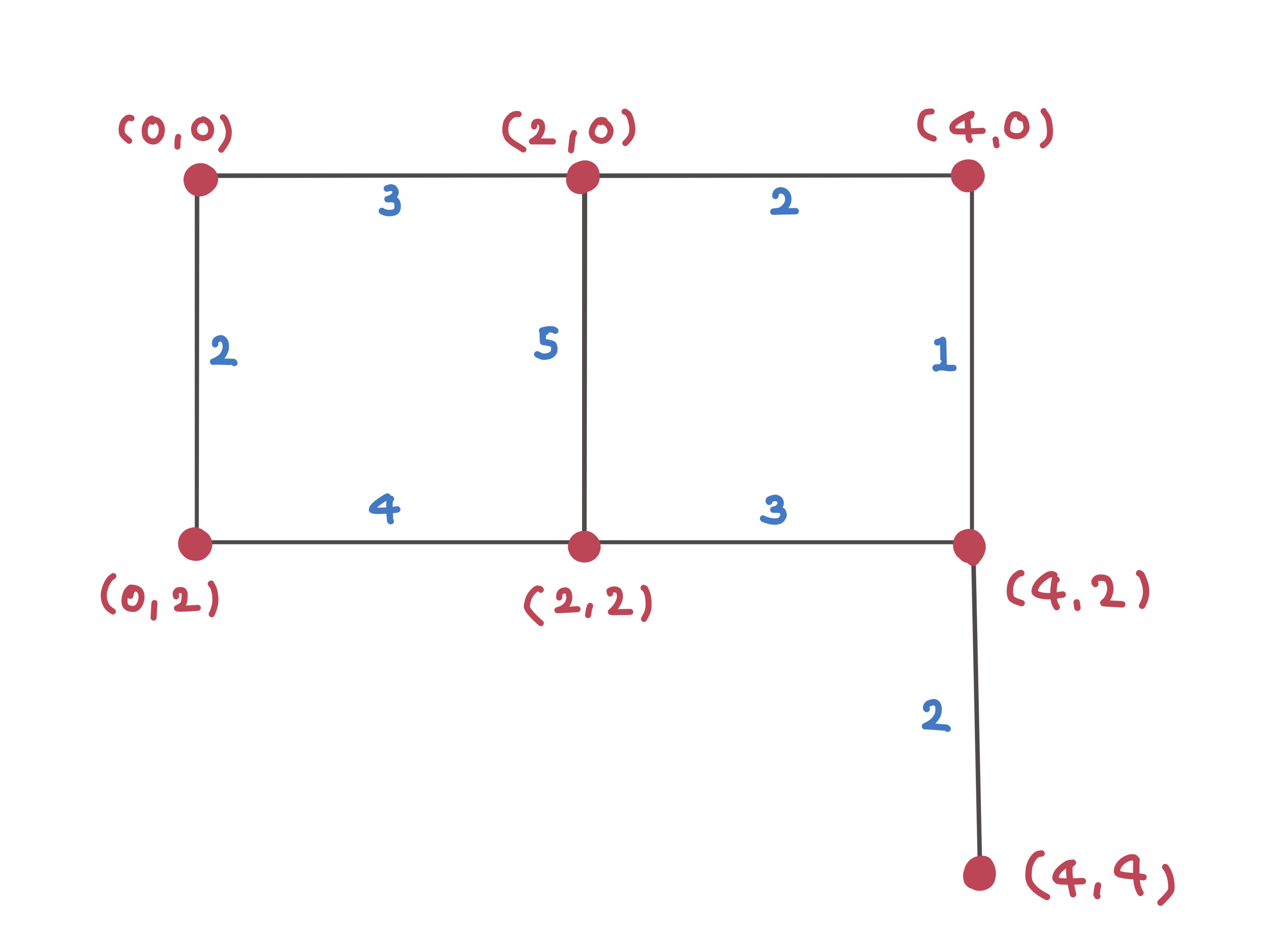
Python으로 A* 알고리즘 구현한 것과 마찬가지로 같은 그래프를 사용했다.

출력된 결과

(0,0) (2,0) (4,0) (4,2) (4,4) 
총 가중치 합 : 8

마치며

와... C++로 dijkstra 코딩할 때보다 이번이 훨씬 어려웠다. 기억나지 않는 C++을 붙잡고 엄청나게 씨름했다. 애초에 그때 배웠던 C++ 지식이 남아있다 하더라도 이 정도의 알고리즘을 내가 구현할 수 있었을 것 같지도 않다.
이번 포스트에서 코드 설명을 상세하게 쓴 것은, 내가 일일히 문법적인 부분이나 코드 디자인을 한 이유들을 기억하지 못할 것 같아서 그렇다.
Python으로 코딩할 때는 거의 '뇌를 반쯤 빼고' 흘러가듯이 해도 어느정도 괜찮은 코드가 완성되는데, C++은..... 잘 하려면 정말 많은 노력이 필요할 것 같다.