Dijkstra 알고리즘 in C++

Dijkstra 알고리즘 in Python

이전 글에서는 Dijkstra 알고리즘을 나에게 가작 익숙한 언어인 Python으로 구현해보았다.
C++은 20살 이후로 처음 써보는데, 그 당시에는 A학점을 받았지만 지금 다시 써보려니 어색하고 낯설다.
또한 맥북에서 C++을 사용하려니 맥용 비주얼 스튜디오는 지원이 중단되어서 VSCode 익스텐션을 사용해야 하는데 이 설정 과정이 좀 번거로웠다.

아무튼, 이번에는 Dijkstra 알고리즘을 C++로 구현해보겠다.

---

C++ 표준 라이브러리의 priority_queue를 활용하여 Dijkstra 알고리즘을 구현할 것이다.
(시작 노드로부터 다른 모든 노드까지의 최단 거리 계산)

Priority Queue

priority_queue 의 기본 개념

• priority_queue는 C++ 표준 라이브러리(STL)에서 제공하는 우선순위 큐 자료구조이다. 이 큐는 가장 높은 우선순위를 가진 요소가 먼저 나오도록 정렬된다.
• C++의 priority_queue는 기본적으로 최대 힙(max heap) 구조로 구현되어, 가장 큰 값이 우선순위를 가지는 형태이다.

Dijkstra 알고리즘에서의 priority_queue

Dijkstra 알고리즘에서는 최단 거리를 기준으로 가장 우선순위가 높은 (가장 거리가 짧은) 노드를 먼저 처리해야 한다. 따라서 최소 힙(min heap) 형태의 priority_queue를 사용하여 최단 거리를 가진 노드를 선택하도록 한다.

C++의 priority_queue 는 기본적으로 최대 힙이므로, 최소 힙을 만들기 위해 greater<type>를 사용하여 우선순위를 반전시켜야 한다.

priority_queue의 주요 함수

• pq.push(item) : 큐에 item을 삽입한다.
• pq.top() : 현재 가장 높은 우선순위를 가진 요소를 반환한다.
• pq.pop() : 현재 가장 높은 우선순위를 가진 요소를 제거한다.(반환 X)

priority_queue의 시간 복잡도

• 삽입(push) : $O($$log$ $N)$
• 제거(pop) : $O($$log$ $N)$
• 최상위 요소 접근(top) : $O(1)$

---

전체 코드

#include <iostream>
#include <vector>
#include <queue>
#include <unordered_map>
#include <limits>

using namespace std;

// node, weight 설정을 위한 pair 정의
typedef pair<int, int> pii;

// Dijkstra 알고리즘 함수
unordered_map<int, int> dijkstra(const unordered_map<int, vector<pii>>& graph, int start) {
    // 각 노드까지의 최단 거리를 저장하는 unordered_map (초기값 : 무한대)
    unordered_map<int, int> distances;
    for (const auto& node : graph) {
        distances[node.first] = numeric_limits<int>::max();
    }
    distances[start] = 0;

    // 우선순위 큐 초기화 (first : 거리, second : node 인 pair)
    priority_queue<pii, vector<pii>, greater<pii>> pq;
    pq.push({0, start});

    while (!pq.empty()) {
        int current_distance = pq.top().first;
        int current_node = pq.top().second;
        pq.pop();

        // 이미 처리된 노드라면 건너뛴다
        if (current_distance > distances[current_node]) {
            continue;
        }

        // 인접한 노드와 가중치 확인
        for (const auto& neighbor : graph.at(current_node)) {
            int adjacent = neighbor.first;
            int weight = neighbor.second;
            int distance = current_distance + weight;

            // 최단 거리를 갱신할 수 없는 경우
            if (distance < distances[adjacent]) {
                distances[adjacent] = distance;
                pq.push({distance, adjacent});
            }
        }
    }

    return distances;
}

int main() {
    // 그래프 정의 (인접 리스트 형태)
    unordered_map<int, vector<pii>> graph;
    graph[1] = {{2, 2}, {3, 4}};
    graph[2] = {{1, 2}, {3, 1}, {4, 7}};
    graph[3] = {{1, 4}, {2, 1}, {4, 3}};
    graph[4] = {{2, 7}, {3, 3}};

    int start_node = 1;
    unordered_map<int, int> distances = dijkstra(graph, start_node);

    cout << "노드 " << start_node << "에서 다른 노드까지의 최단 거리 : \n";
    for (const auto& [node, distance] : distances) {
        cout << "노드 " << start_node << "에서 노드 " << node << "까지의 거리 : ";
        if (distance == numeric_limits<int>::max()) {
            cout << "도달 불가\n";
        } else {
            cout << distance << "\n";
        }
    }

    return 0;
}

C++의 최신 문법에도 적응하지 못해서 완전 애먹었다. 아무래도 C++을 제대로 사용하려면 많은 공부가 필요할 것 같다.

---

코드 상세 구조

헤더

#include <iostream>
#include <vector>
#include <queue>
#include <unordered_map>
#include <limits>

• iostream : Console의 입출력 기능
• vector : 인접 노드를 저장하기 위해 사용
• queue : Dijkstra 알고리즘에서 우선순위 큐를 구현하기 위해 priority_queue를 사용하기 위함
• unordered_map : 그래프의 인접 리스트와 최단 거리를 저장하기 위해 사용.
• limits : 거리 초기화에 무한대 값을 사용하기 위해 numeric_limits를 포함한다

여기서 unordered_map은 키-값 쌍을 저장할 때 사용하는 자료구조다. 해시 테이블 기반으로 구현되어 데이터가 정렬되지 않고 저장되고, 데이터를 저장할 때 각 키가 특정 해시값으로 매핑된다는 점에서 map과 차이가 있다.

// node, weight 설정을 위한 pair 정의
typedef pair<int, int> pii;

• typedef pair<int, int> pii : pair<int, int>를 pii라는 타입 별칭으로 작성함. pair<int, int>의 첫번째 int는 node, 두번째 int는 가중치이다.

---

함수 정의

// Dijkstra 알고리즘 함수
unordered_map<int, int> dijkstra(const unordered_map<int, vector<pii>>& graph, int start) {

• 함수의 목적 : Dijkstra 알고리즘을 사용해서, 시작 노드에서 모든 다른 노드까지의 최단 거리를 계산하고, 결과를 unordered_map 형태로 반환한다.
• 매개변수 :
  • graph : 인접 리스트 형태로 표현된 그래프. 각 노드의 연결관계와 가중치를 저장한다.
  • start : 알고리즘이 시작되는 노드 번호

    unordered_map<int, int> distances;
    for (const auto& node : graph) {
        distances[node.first] = numeric_limits<int>::max();
    }
    distances[start] = 0;

• distances 초기화 :
  • distance는 각 노드까지의 최단 거리를 저장하는 unordered_map이다. 각 노드의 거리를 초기화하여 시작 노드는 0, 나머지 노드는 무한대로 설정한다.
  • numeric_limits<int>::max() : 무한대를 표현하기 위한 값

---

우선순위 큐 설정

    while (!pq.empty()) {
        int current_distance = pq.top().first;
        int current_node = pq.top().second;
        pq.pop();

• 반복문
  • 큐가 빌 때까지 반복한다. pq.top()을 통해 현재 최단 거리의 노드와 거리를 가져온다.
  • current_distance는 현재 노드까지의 거리, current_node는 현재 노드

        // 이미 처리된 노드라면 건너뛴다
        if (current_distance > distances[current_node]) {
            continue;
        }

• 이미 처리된 노드 건너뛰기 : 만약 현재의 current_distance가 distances[current_node] 보다 크다면, 이미 최단 거리가 확정된 노드이므로 탐색하지 않고 건너뛴다. (큐에 중복으로 들어가는 불필요한 경로들을 처리하는 것을 막아서, Dijkstra 알고리즘의 효율성을 높인다)

---

인접 노드 탐색 및 거리 갱신

        // 인접한 노드와 가중치 확인
        for (const auto& neighbor : graph.at(current_node)) {
            int adjacent = neighbor.first;
            int weight = neighbor.second;
            int distance = current_distance + weight;

            // 최단 거리를 갱신할 수 없는 경우
            if (distance < distances[adjacent]) {
                distances[adjacent] = distance;
                pq.push({distance, adjacent});
            }
        }

• for 루프
  • 현재 노드의 인접 노드를 탐색한다. neighbor.first는 인접 노드의 번호, neighbor.second는 해당 경로의 가중치
  • distance = current_distance + weight를 통해 현재 노드에서 인접 노드로 이동할 때의 새로운 거리를 계산한다
• 거리 갱신
  • 새로운 거리가 기존의 최단 거리보다 작으면, distances[adjacent]을 새로운 거리로 갱신한다.
  • 갱신된 인접 노드는 우선순위 큐에 추가되어, 다시 최단거리 우선으로 탐색되도록 한다.

---

함수 반환

    return distances;

• 모든 노드까지의 최단 거리가 저장된 distance 맵을 반환한다.

---

메인 함수 및 출력

int main() {
    // 그래프 정의 (인접 리스트 형태)
    unordered_map<int, vector<pii>> graph;
    graph[1] = {{2, 2}, {3, 4}};
    graph[2] = {{1, 2}, {3, 1}, {4, 7}};
    graph[3] = {{1, 4}, {2, 1}, {4, 3}};
    graph[4] = {{2, 7}, {3, 3}};

    int start_node = 1;
    unordered_map<int, int> distances = dijkstra(graph, start_node);

    cout << "노드 " << start_node << "에서 다른 노드까지의 최단 거리 : \n";
    for (const auto& [node, distance] : distances) {
        cout << "노드 " << start_node << "에서 노드 " << node << "까지의 거리 : ";
        if (distance == numeric_limits<int>::max()) {
            cout << "도달 불가\n";
        } else {
            cout << distance << "\n";
        }
    }

    return 0;
}

• 그래프 정의 : unordered_map으로 그래프를 정의한다. 각 노드와 연결된 다른 노드와 그 간선의 가중치를 인접 리스트 형태로 저장한다. 대략 아래 그림과 같은 형태다.
  

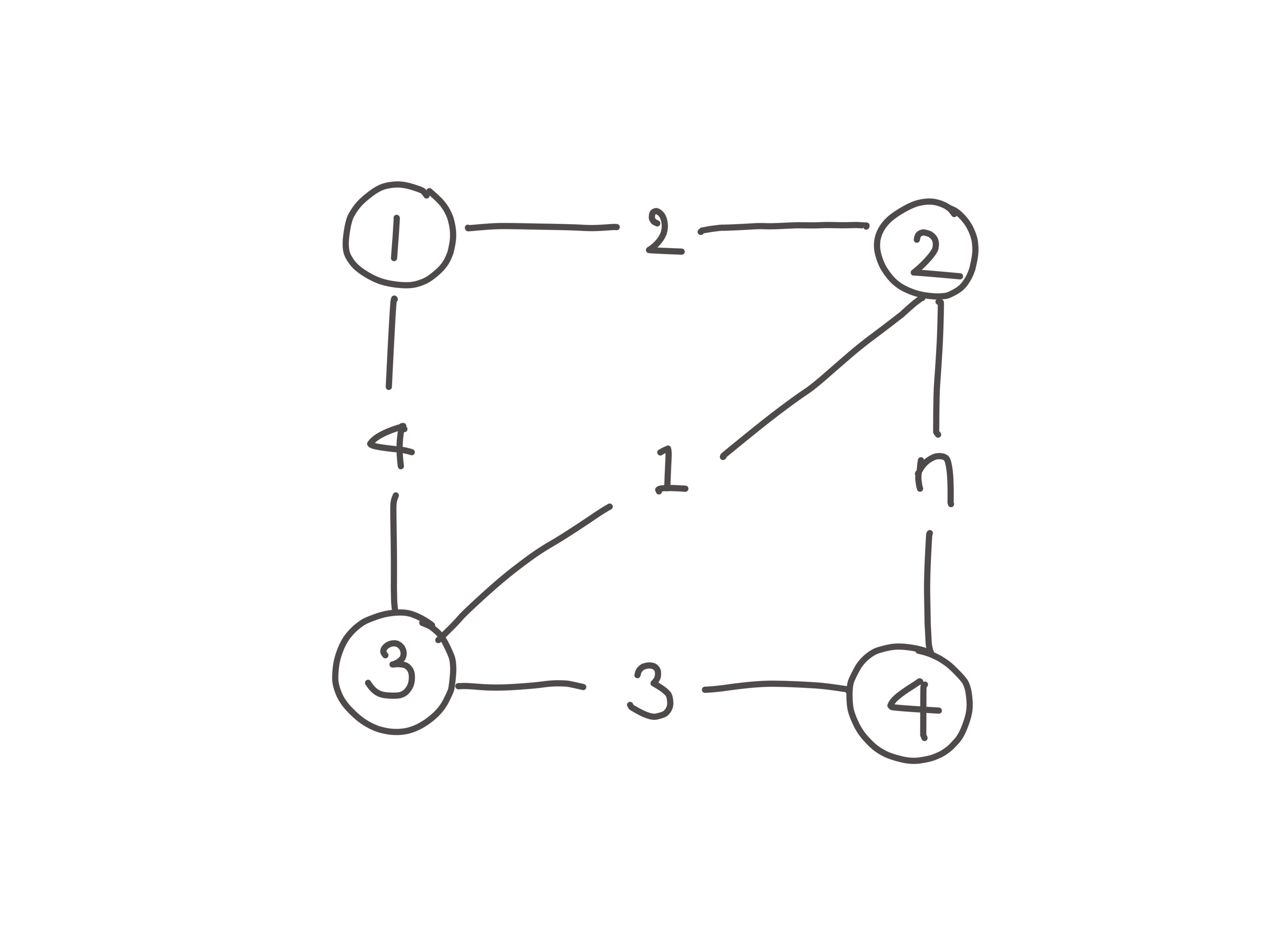
• 출력

  • Dijkstra 함수의 결과로 반환된 distances 맵에서 시작 노드로부터 각 노드까지의 최단 거리를 출력한다.
  • 만약 최단 거리가 무한대(numeric_limits<int>::max())라면, 해당 노드에 도달할 수 없음을 의미하여 "도달 불가" 로 출력한다.