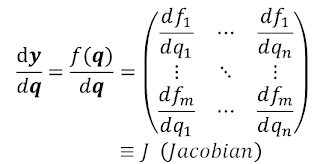최근에 특정 layer층의 가중치를 Masking하는 방법에 대해서 알아보고 있던 도중에
discussion
을 확인하게 됐다. 이전에도 autograd가 gradient를 조정하는 역할을 하는 것을 알고는 있었는데, 정확히 알지는 못했기 때문에 이 기회에 정리해보고자 한다.
tutorial
을 참고했다.

AutoGrad?

Autograd ; Automatic gradient calculating API

AutoGrad의 미분

우선 우리는 파이토치 tensor가 requires_grad라는 속성을 갖는 것을 알고 있다. 이것이 일종의 마킹의 역할로 Autograd에게 연산을 추적해야 한다고 알려준다.

import torch

a = torch.tensor([2., 3.], requires_grad=True)
b = torch.tensor([6., 4.], requires_grad=True)

이때, a와 b는 신경망의 매개변수(즉, 가중치)라고 하자.
a와 b를 통해서 새로운 텐서 Q를 만들자.

Q = 3*a**3 - b**2

이때, Q는 Error라고 해보자 우리는 backward()를 통해서 loss를 BackPropagation 시키는데, 이 과정에서 $\frac {dQ} {da}=9a^2$ 와 $\frac {dQ} {db}=-2b$를 구해야 한다.
현재 Q는 vector이기 때문에 중간 Layer라고 생각하고 전파되는 gradient($\frac {dQ} {dQ}$)를 제공해줘야 한다. 이를 backward()의 gradient 파라미터로 제공하면 된다.

실제 Pytorch에서는 하나의 Loss Tensor를 계산하는 과정을 Computational Graph로 저장해두고 계산된 loss를 Backward 시키면서 loss Tensor의 .grad를 이전의 파라미터들의 편미분 값으로 계산해서 저장해 두는데, 여기서는 벡터로 나와서 loss를 산출해내는 과정이 없기 때문에 gradient 파라미터를 제공해 주어야 하는 것이다.

external_grad = torch.tensor([1., 1.])
Q.backward(gradient=external_grad)

Q.backward()를 통해 변화도는 a Tensor의 a.grad와 b Tensor의 b.grad에 저장된다.
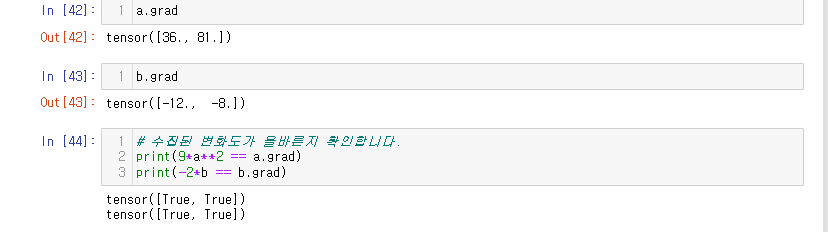
다음과 같은 결과를 통해서 AutoGrad가 적절하게 BackPropagation을 시켰음을 확인할 수 있다.

AutoGrad의 Calculus

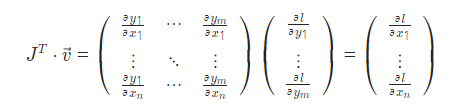
tutorial에서는 벡터함수에 대한 야코비안 행렬 J를 도입해서 AutoGrad의 역할을 설명한다.

야코비안 행렬(Jacobian Maxtrix) ?
다변수 벡터 함수에서의 미분값으로써 생각하면 된다.
좀 더 쉽게 설명하자면 변수를 여러개 갖는 output을 벡터 형태로 내는 함수를 미분을 해서 행렬 형태로 만들어 놓은 것이다.

자, 우리는 이런 연쇄법칙과 야코비안 행렬의 곱을 통해 loss에 대한 각 middle층 가중치를 업데이트 해나갈 수 있는 것이다.

연산그래프(Computational Graph)

autograd는 텐서에 적용된 계산의 history를 Function 객체로 구성된 방향성 비순환 그래프(DAG; Directed Acyclic Graph)에 저장한다. 이 방향성 그래프의 leaf노드는 입력 텐서이고 root 노드는 결과 텐서이다. 이 그래프를 root 부터 추적하면 gradient를 계산할 수 있다.

import torch

a = torch.tensor([2.0], requires_grad=True)
b = a ** 2
c = b * 3
d = c.mean()

print(d.grad_fn)

다음과 같은 상황에서 .grad_fn은 pytorch에서 autograd를 위해 계산 그래프를 구성하는데 사용되는 속성으로써 위의 예시에서 d.grad_fn을 출력하면 MeanBackward()와 같이 연산의 타입을 나타내는 값이 될 것이다. 이렇게 d의 .grad_fn을 따라가면서 gradient를 계산하여 gradient를 쌓은 이후 연쇄법칙을 사용해서 이전의 연산들인 c,b,a를 찾아갈 수 있다.

DAG를 시각적으로 표현하면 다음과 같다.

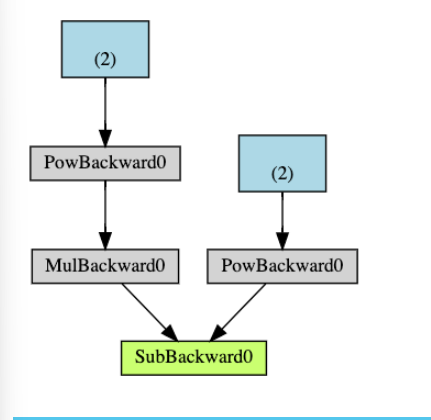
DAG에서 제외하고자 하면 requires_Grad=False로 설정해두면 된다.

참고할점은 .backward()를 call하면 call하는 순간 autograd는 graph를 새로 만들기 시작한다는 것이다.

backward()의 retain_graph = True라는 파라미터는 DAG와 연결지어 생각해보면 backward를 한번수행하면 또 다시 backward를 수행할 수 없는데, 이때 그래프를 유지하게 해서 두가지 loss에 대해서 backward를 수행할 수 있게 된다.
링크