Part of XAI(1)

이성준·2023년 9월 6일

XAI

목록 보기

1/1

이 글의 References

XAI관련 Velog는 XAI를 공부하기 위해서 위의 책을 참고하고자 했는데, 너무 제한적인 설명때문에 구글링을 찾아봤고 일부는 직접 논문을 읽었다.
시작하겠다.

Introduction

XAI는 Explanable AI로써 우리는 딥러닝 모델들의 결과가 왜 이렇게 나온건지에 대한 설명을 할 수 없었다. 이러한 문제를 해결하기 위해서 나온 기술이고 파이썬의 XAI 라이브러리인 LIME과 SHAP등을 안내할 것이다.
책을 통해 얻을 수 있는점

→ AI의 책임성
→ AI를 어떤 업무에 적용할 때 어떤 설명이 필요한지
→ XAI의 전역 설명과 국소 설명을 구분해 사용 가능
→ XAI의 목표와 작동원리를 수식으로 파악하고 주요기법의 장단점 및 다루는 데이터나 풀어야할 Task에 따른 모델의 성능 차이
→ 어떤 Task가 갖는 데이터의 특성, AI알고리즘, 성능 요건등에 따라 적절한 XAI기술 선정

1.1 AI 보급과 새로운 요구 사항

AI 활용의 대상인 ‘인식’과 ‘분류’ ‘예측’이라는 요소에서 지금까지 중요하다고 여겨진 것은 바로 “정확도” 였다. 하지만 지금에 와서는 AI에 정확도 이외의 가치도 요구되기 시작됐다.
우리는 AI의 발전으로 인해서 일자리가 대체될 것이라고 말을 해왔지만 실제로 그러한 일은 거의 발생하지 않았다. 왜 그럴까? 그 이유를 저자는 다음과 같이 설명한다.
먼저 대전제는 AI도 일종의 소프트웨어이다. 우리는 다른 소프트웨어는 Input에 대한 Output값을 추적을 통해 설명할 수 있다. 하지만 AI는 데이터를 통한 “학습”에 의해 이 데이터도 이전의 학습한 Boundary안에서 찾는 것이다. 따라서 역추적하기가 어렵다. AI는 일종의 패턴을 학습하는 것이라고 볼 수 있기 때문에, 학습 데이터에 맞추어서 유연한 처리 방법을 학습 할 수 있기 때문에, 사람의 업무에 AI를 적용하는 경우가 늘어난다. 하지만 우리의 의사결정에 AI가 관여하는 것에 대해서 출력결과의 공평성이나 윤리적 타당성이 요구되고 있다.
AI의 활용의 확대에 따라서 요구되는 가치는 3가지가 있다

Fairness(공평성)
Accountability(책임성)
Transparency(투명성)

2장 XAI의 개요

2.1. XAI란 무엇인가?

XAI는 어떠한 특정 기술이나 도구를 지칭하는 말이 아니고 다양한 종류의 AI를 다양한 관점에서 이해한다는 목적을 위해 개발된 기술이나 도구들을 총칭하는 말이다.

2.2 설명 가능한 AI (Explanable AI)와 해석 가능한 AI(Interpretable AI)

$InterpretableAI⊂XAI$
설명가능한 AI(Explanable AI)

AI 모델의 내부를 정교하게 해석할 필요는 없고, AI가 도출한 결과에 대한 이유를 설명하는 기술을 나타낸다.
Ex)
데이터의 어떠한 부분이 중요한가?
판단 기준이 되는 요소에는 어떠한 것이 있는가?

해석가능한 AI(Interpretable AI)

위에 설명가능한 AI와는 다르게 내부구조를 해석함으로써 예측에 이르는 계산 과정을 확인할 수 있는 AI
EX)
고전적인 의사결정 트리

2.3. XAI의 설명 범위에 따른 분류

XAI를 활용한 AI의 설명은 설명 범위에 따라 구분된다.

전역 설명(Global Explanation)

AI 모델의 전체적인 동작을 이해하는 것을 목적으로 하는 설명 방법이다.
→ 하나 하나의 데이터에 대한 예측과정을 설명하는 것이 아니고, General하게 나타나는 AI 내부의 지배적인 경향을 나타낸다.
Ex>
1. Feature 별 예측에 대한 중요도 산출
2. AI의 logic을 가시화

위의 예시와 같은 Global Explanation에 따른 AI의 이해는 모델 자체의 평가나 학습 개선을 야기한다.

국소 설명(Local Explanation)

어떠한 데이터에 대한 예측 결과를 설명하는 것이다.
Ex>
구체적으로 어떠한 사례에 대한 AI의 예측 데이터에 기록된 몇 개의 변수에 대해 각 예측 확률을 어느 정도 높이냐에 따라 ‘기여도’를 산출해 예측의 판단 결과를 설명한다.

전역설명의 ‘Feature별 예측에 대한 중요도 산출’과 국소 설명의 ‘예측 데이터에 기록된 변수의 기여도를 산출’의 차이 ?
→ 다르게 생각해보면 전체 데이터에 대해서 기여도 산출 <-> 전역설명
일부 데이터에 대해서 기여도 산출 <-> 국소설명

2.4. XAI의 설명 방법에 따른 분류

1. Feature를 활용한 설명

어떤 입력 데이터에 대해 Feature가 예측 결과에 어느 정도 영향도가 있는지를 산출
이는 데이터의 종류에 따라 표에서는 중요한 Feature를 표시하는 방식으로 이미지에서는 중요한 부분을 marking 하는 방식으로 나타날 수 있다.
E.g.) 허스키와 늑대의 사진을 보고 눈을 보고 판단을 했다~.. 와 같이 눈 부분이 marking된 경우

2. 판단 규칙을 활용한 설명

EX> 의사결정트리
인간이 이해할 수 있을 정도의 규칙의 수여야 한다.

3. 학습데이터를 활용한 설명

이는 이미지 데이터를 기준으로 이해하면 좋다.
여러 이미지 학습데이터가 주어질텐데, 가장 많이 참고한 학습데이터를 제시함으로서 판단 이유의 설명으로 나타낸다
Effect) 예측에 악영향을 미치는 학습 데이터를 제거할 수있다

2.5. 모델 의존성

모델 의존형 XAI와 모델 불문형 XAI

모델 의존형 XAI는 특정 모델을 설명하는 XAI로써 모델의 구조를 활용하여 설명할 수 있고

모델 불문형 XAI(model agnostic XAI)는 대상 모델의 제약이 없어 모델에 상관없이 어떤 데이터가 입력됐을 때 어떤 예측이 나오는지 관계성을 파악하도록 한다.

따라서 모델의 상관없이 일괄적으로 설명할 수 있지만, 모델의 구조를 사용하지 않기 때문에 모델 의존형 XAI보다는 합리적인 설명을 할 수 있는 가능성이 떨어지게 된다.

3장 XAI의 활용 방법

3.1. 설명 범위별 활용 방법

국소설명(local explanation)

1. 신고 내용의 타당성 검증
Ex) 화물의 신고서를 AI가 검토한다고 했을 때, 우리는 화물에 대해 신고품목의 종류, 중량, 부피등의 데이터를 AI에게 제공할 수 있다. 이때 종류, 중량, 부피중에서 거절에 중요한 순서로 나열해서 손님에게 제공할 경우 거절을 설명할 수 있다.
각 손님마다 중요한 순서가 다르기 때문에, local explanation이다.

2. 의도와 다른 학습 재검토

위에 사진을 보면 그림은 허스키인데 AI모델이 늑대로 잘못 분류한 상황이다. 이때, 그렇게 분류한 이유를 설명한 그림이 b인데 배경의 눈을보고 이 그림이 늑대라고 분류한 것이다.
이는 데이터의 불균형에 의한 문제라고 볼 수 있고, 이것이 바로 ‘의도와 다른 학습’이다.
또한, 올바르게 분류 혹은 예측을 수행했더라도 XAI를 통해 나온 그 이유가 도저히 말이 안되는 이유가 제시 된다면 바로 잡아야 한다

전역 설명(global explanation)

1. AI 모델의 개선 운용
실제 시스템에 적용되는 AI 모델에는 지속 운용을 위한 유지보수가 필요하다.
구축할 당시에는 최적의 상태로 AI모델이 세팅이 되겠지만, 데이터의 경향(Trend)의 변화가 생기거나하면 정밀도에 문제가 생길 수 있다.
따라서 모델의 지속 운용을 위한 유지보수가 필요하게 되는데, 이러한 유지보수간에 모델의 예측을 설명할 방법이 없다면, 모델의 개선을 할 수가 없기 때문에 XAI를 활용하게 된다.

2. 적대적 공격 검증
현재 AI에서 특히 우려가 되고 있는 문제중 하나가 적대적 공격(Adversarial Examples)이 있다.
적대적 공격 이란?

팬더의 이미지에 노이즈를 더하니깐 긴팔 원숭이로 인식하는 것을 볼 수 있다. 위와 같이 AI의 오인식을 유도하는 방법을 적대적 공격이라고 한다.
또다른 예로써 노이즈를 더함으로써 강아지를 물고기로 잘못 인식하는 사례가 있다.

위의 사진을 설명해보자면 우리는 파란색 박스의 강아지를 물고기로 예측하도록 하게 하기 위해서 노이즈를 더해서 물고기로 예측을 하도록 하니, 아래 빨간색 박스 위의 강아지들이 모두 물고기로 예측이 됐음을 볼 수 있다.

우리는 위와 같이 XAI를 통해 적대적 공격을 재현하고 파란색 박스의 이미지가 중요한 역할을 담당하고 있다는 사실을 알 수 있고, 이를 통해 적대적 공격에 대비할 수 있게 한다.

다양한 XAI 기술

LIME(Locally Interpretable Model-agnostic Explainations)

👉🏻 LIME은 전체적인 모델의 예측에 대해 분석하지는 않는다. 어떠한 설명 대상 데이터 1건에 대해 AI모델의 예측에 기여한 Feature들의 기여도를 산출한다. local explanation

👉🏻 LIME은 Model Agnostic하다.

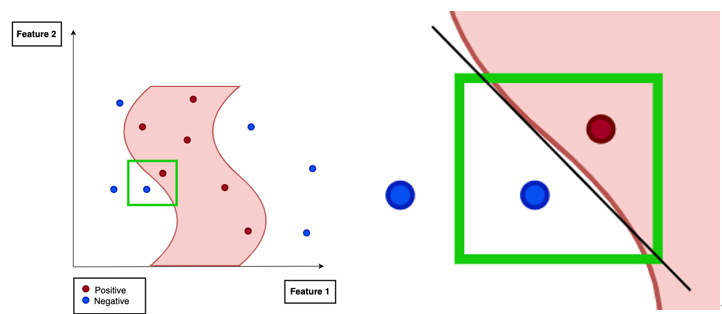
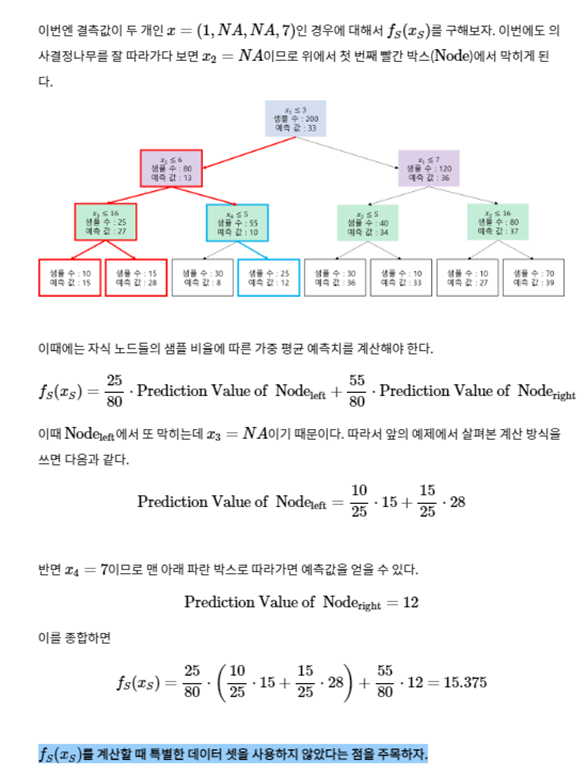
왼쪽 그림과 같이 positive인 부분과 negative인 부분의 경계는 매우 복잡해서 설명할 수 있는 가능성이 떨어진다. 이때, 우리는 설명 대상 데이터를 포함한 Local한 부분(오른쪽 영역)만 관찰하겠다는 것이다.

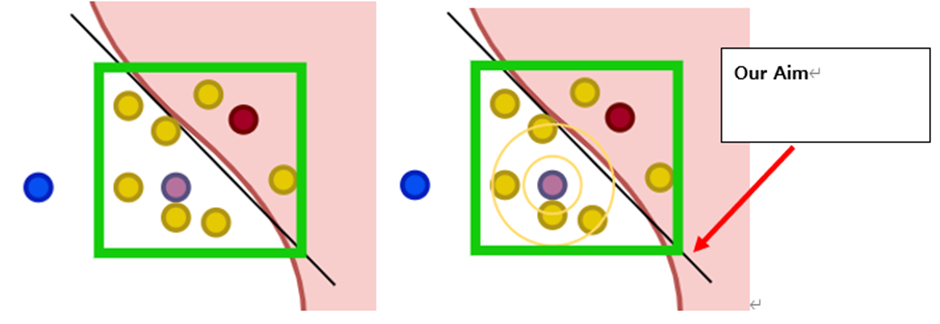
왼쪽 그림과 같이 노란색 Point들을 다수 작성해서 우리의 AI 모델을 이용해 이 노란색 포인트들을 예측(위의 그림에서는 분류)를 수행한다.

AIM: 우리의 목표를 다시한번 상기하자면 저 보라색 Point를 우리의 모델이 예측하는 결과가 왜 그렇게 나오는지 이유를 제시하는 것이 목표이다. -> 이를 위해 선형모델을(surrogate model)을 구하는 것이 목표이다.(해석을 위한 대리모델 = surrogate Linear model)

위와 같은 AIM때문에 우리는 Local한 영역을 잡았고, 임의의 point를 생성한것이다

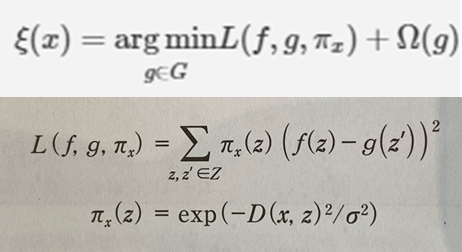
우리는 위에서 언급한 surrogate model을 구하기 위해서 위와 같은 수식을 Loss Function으로 사용하게 됐다.
위에 오메가 Term은 regularization term으로써, Ridge 회귀를 사용한다

위의 수식을 이해하려면, L term이 의미하는 것을 이해해야하는데,
우리의 데이터 구조가 Feature1, Feature2에 대해서 각각이 연령, 거주지를 의미하고 설명 대상 데이터 x = (20대,서울) 이라고 해보자
이때, 설명 대상 데이터 근방에 있는 생성 데이터들의 Set을 의미하는 것이 바로 Z이고
여기서 나온 원소들을 z 이러한 z를 모델 g에 넣을 수 있도록 변화시킨( ex> z=(20대, 부산) -> z’=(1,0) ) 벡터가 바로 z’이다.
따라서 해석을 해보자면 우리의 모델로 예측한 것과 surrogate 모델이 예측한 것의 차의 제곱이고, 그 앞에 곱하는 $π_x (z)$ 는 생성한 데이터 z와 설명 데이터 x사이의 거리를 나타낸다.

위와 같은 Loss Function을 이용해서 우리는 surrogate model인 g를 구할 수 있게 됐고, 이는 Linear model이므로 회귀계수가 Feature에 대한 기여도가 되게 된다.

기본적으로 XAI에서 Linear모델은 계수로써 설명이 가능하다는 것이 전제로 깔려있다.

참고

LIME의 데이터 종류별 동작원리

우리는 위에서 근방의 데이터를 통해 surrogate model을 만들었음을 알 수 있다. 따라서 근방의 데이터를 어떻게 생성하는지 위주로 설명하겠다.

테이블 데이터 LIME의 경우

테이블 데이터 같은 경우는 학습 데이터를 LIME에 사전에 입력하고 학습 데이터의 통계적인 계산 정보를 바탕으로 값을 생성하는데, 이때 Feature의 전체 도메인에 무작위로 데이터를 생성하고, 설명 대상 데이터와의 거리가 가까운 데이터를 중요시하도록 해서 실질적인 근방 데이터를 만들게 된다.

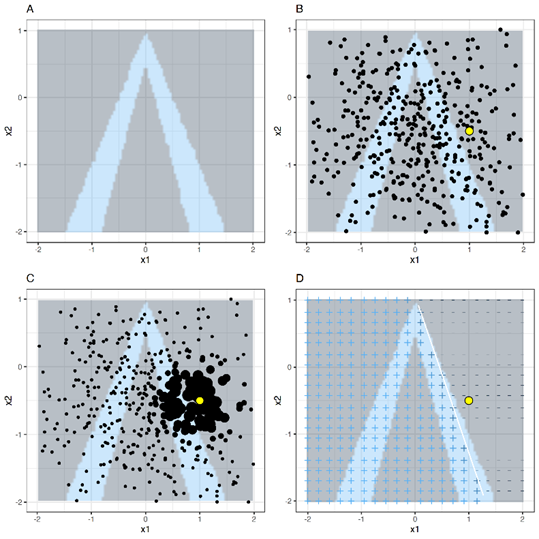
위 그림과 같이, 설명하고자 하는 데이터가 노란색 포인트이고 그 외의 검은색 포인트가 추출된 근방 데이터이다. 이중에서 가까운 데이터들에 가중치를 크게줘 (포인트의 크기를 키워서) 실질적인 근방데이터를 만들게 된다. 이때 어디까지가 의미있는 이웃이냐? 라는 것을 정하는 것이 이슈인데, LIME은 현재 지수 평활 커널(exponential smoothing kernel)을 사용하여 이웃을 정의한다. 평활 커널은 두개의 데이터를 받아서 데이터간의 유사도(similarity)[실제 블로그에서는 근접성 측도 proximity measure 로 언급]를 반환하는 함수이다. 이때 커널 너비는 이웃의 크기를 결정하는데, 이 커널너비의 적절한 크기가 Issue가 된다.

→ 커널너비가 작으면 매우 근접해야 영향을 줄수 있고, 폭이 더 크면 멀리있는 인스턴스도 모델에 영향을 미친다.

이미지 데이터 LIME의 경우

이미지 데이터 같은 경우는 보통 픽셀 단위의 RGB 값을 사용하여 AI 모델에 입력하곤 한다. 하지만 픽셀 단위로 XAI를 적용하게 되면 계산양이 매우 방대해지고, 얻을 수 있는 설명의 결과도 픽셀 단위에선 유의미 하지 않다.
따라서, 이미지 데이터 LIME에서는 세그먼트 라는 영역으로 분할해 세그먼트마다의 모델의 판정 기여도를 산출한다.[책에 따라선 세그먼트가 super pixel로 언급이 돼있다] 이 세그먼트 영역에서는 동일한 정보를 가지고 있다고 간주한다.
근방 데이터의 생성은 세그먼트 단위에서 이미지를 삭제함으로써 생성하는데, 통상적으로 백색이나 흑색, 이미지의 평균값등으로 덧칠하여 해당 세그먼트의 특징을 무효화함으로써 삭제한 것으로 취급한다.

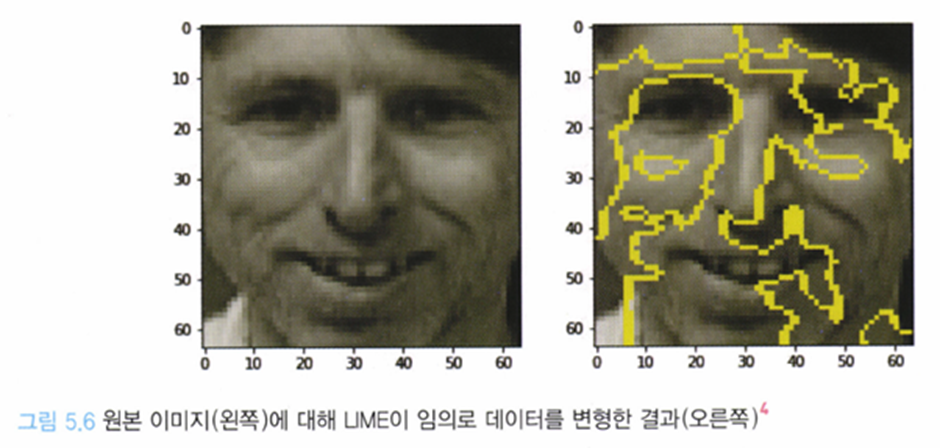
위의 이미지에서 비슷한 색상을 갖은 픽셀들을 연결해서 선을 구성하고 이해단위를 구분한다.

위와 같이 구분을 시킨후 경우의 수를 따져서,
$x_i^{'}$ : 슈퍼픽셀 마스킹 정보(슈퍼픽셀을 포함시키냐, 포함시키지 않냐)
$w_i$ : 슈퍼픽셀의 가중치(영향의 정도)

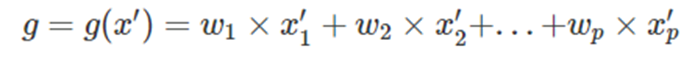
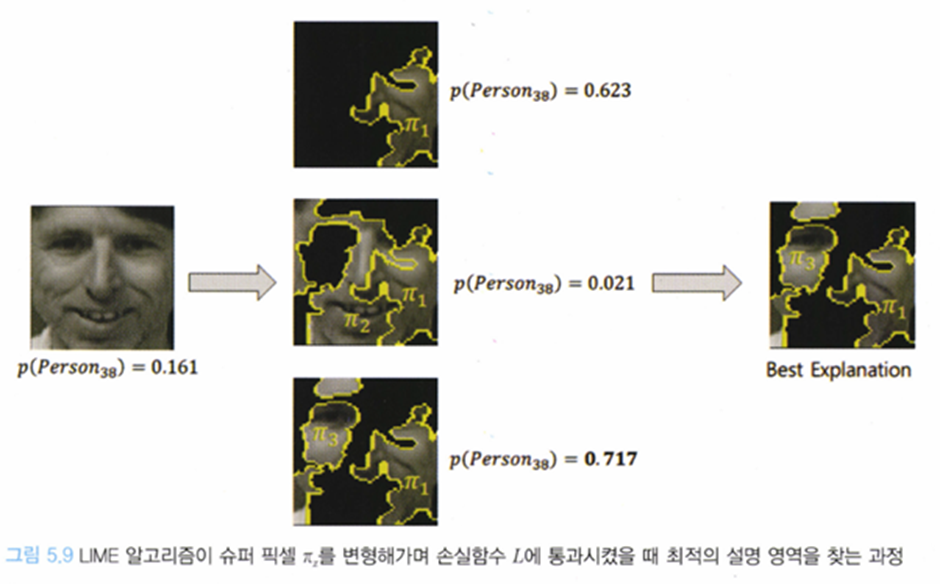
위의 그림에서 손실함수 L을 최소화 하는 슈퍼픽셀의 조합을 구한후 각 슈퍼픽셀에 대한 가중치를 사용해서 얼만큼의 중요도를 갖는지 파악할 수 있다.

텍스트데이터 LIME의 경우

~~위에 두 종류의 데이터에 비해서는 이해의 정도가 그렇게 높지 않다.~~
이 텍스트데이터의 경우에는 블랙박스 모델[설명대상모델]을 의사결정나무를 사용한다.
텍스트 데이터 LIME에서는 하나의 문장에서 일부 단어를 빼고 예측을 함으로써 각 단어가 미치는 기여도를 분석한다. 예를 들어서 유튜브의 댓글을 스팸인지 아닌지 분류하는 경우를 생각해보자.[이때 각 단어를 포함하면 1 빼면 0으로 마킹했다.]

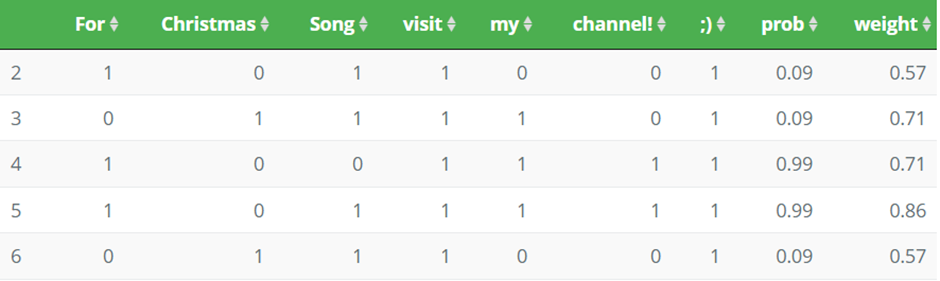
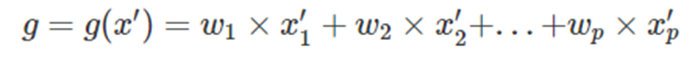
위 식을 이용해서 각 단어를 포함시켰을때와 포함시키지 않았을때를 사용해 weight를 구해서 다음과 같이 특정 단어를 포함할 경우에 spam으로 분류할 확률을 제공한다.

LIME의 장단점

장점:
설명 대상 모델의 종류에 제약이 없다[다른 XAI기술 대부분은 모델이 바뀌면 설명방법도 바뀌어야 한다.]{Model Agnostic}
단점:
1. 근방 데이터를 무작위로 생성하기 때문에 설명 결과가 매번 달라진다.
→ 근방 데이터의 생성 수를 늘리면 결과의 불규칙성을 줄일 수 있다.
2. 하이퍼 파라미터를 조정해야한다.
→ 위에서 언급했듯이 커널크기를 휴리스틱하게 조절해야한다.
3. 정확하게 설명하지 못하는 경우가 있다.
→ 데이터 구조나 모델 구조상 local한 설명을 잘 하지 못하는 경우가 있다. 하이퍼파라미터를 조절해도 여의치 않다면 다른 방법을 검토!

Shapley Value

SHAP을 이해하기 위해서는 Shapley Value에 대해서 알아야 한다.
Shapley value는 게임이론에서 나왔다.

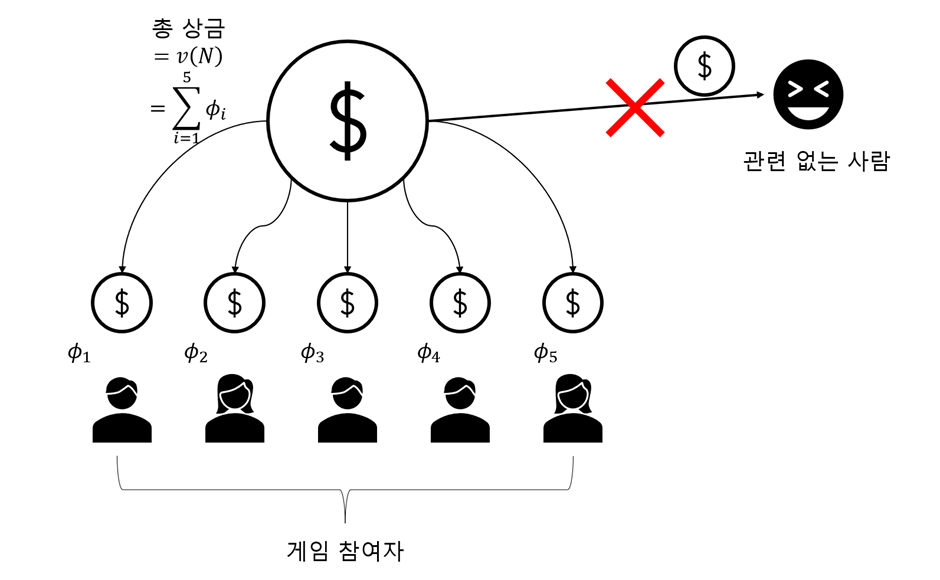
다만, 어떻게 하면 “기여도에 따라” 공정하게 보상을 나눌까? 를 한번 생각해보면 좋겠다. 물론 n으로 나누는 것도 좋을텐데 이는 바람직하지는 않다. 노력을 한것과 안한것과 보상이 같다면 억울해지는 사람이 있기 때문이다. 따라서 몇가지 바람직한 성질들을 정의 하였는데 다음과 같은 것들이 있다.

여기서 상금을 기여도라고 해석

[한눈에 보기 1]

Efficiency – 참가자들의 리워드의 합 = 총 리워드
Symmetry – 두플레이어의 기여하는바가 같다면(꼈을 때 예측값이 같다면) 기여도 또한 같음
Dummy player – 어떤 플레이어를 끼고 안끼고 결과가 똑같다면, 그 플레이어의 기여도는0
Linearity - 기여도는 Linear한 성질이 있음

전체합리성(efficiency)

→ 분배된 보상(기여도)의 합은 총 보상의 합과 일치한다.

대칭성(symmetry)

→ 두 플레이어의 기여도가 같다면 두 플레이어가 가져야 할 상금도 같아야한다.

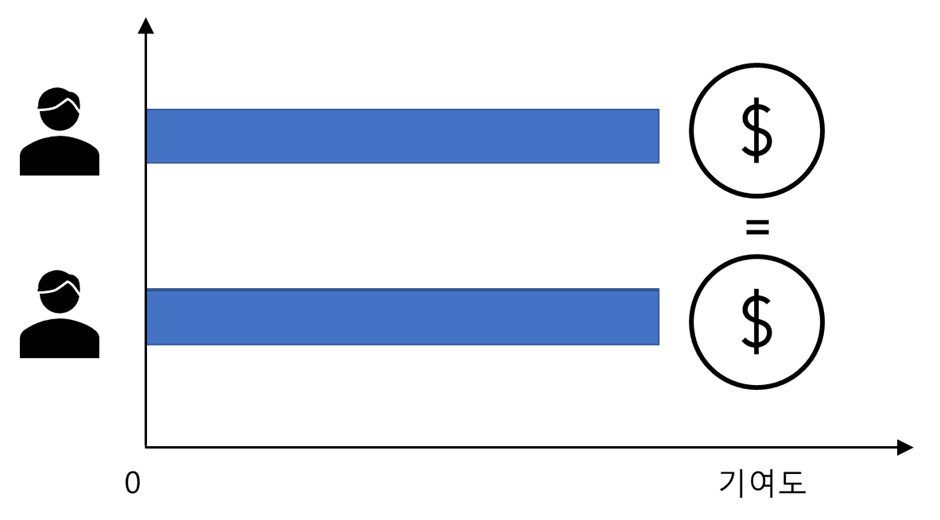
위장 플레이어(Dummy Player)

→ 위장 플레이어(Dummy Player)에게는 보상X

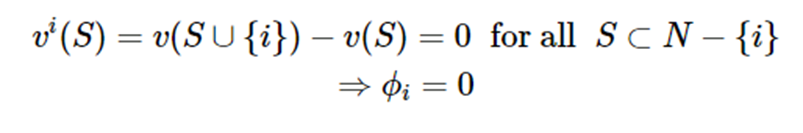
V가 보상이라고 했을 때, S는 참여를 했다고 한 플레이어들의 집합이고 i는 기여를 하지 않았다고 의심이 되는 플레이어라고 하자. i가 받는 보상은 $SU{i}$ 가 받는 보상에서 S가 받는 보상을 뺀것과 같을 것이라고 예상된다. 이때, i는 기여를 하지 않았으므로 두 보상은 같게 되고 따라서 $v ^{i} (s)=0$ , 즉 i가 받는 보상은 0이 된다.

가법성(Linearity)

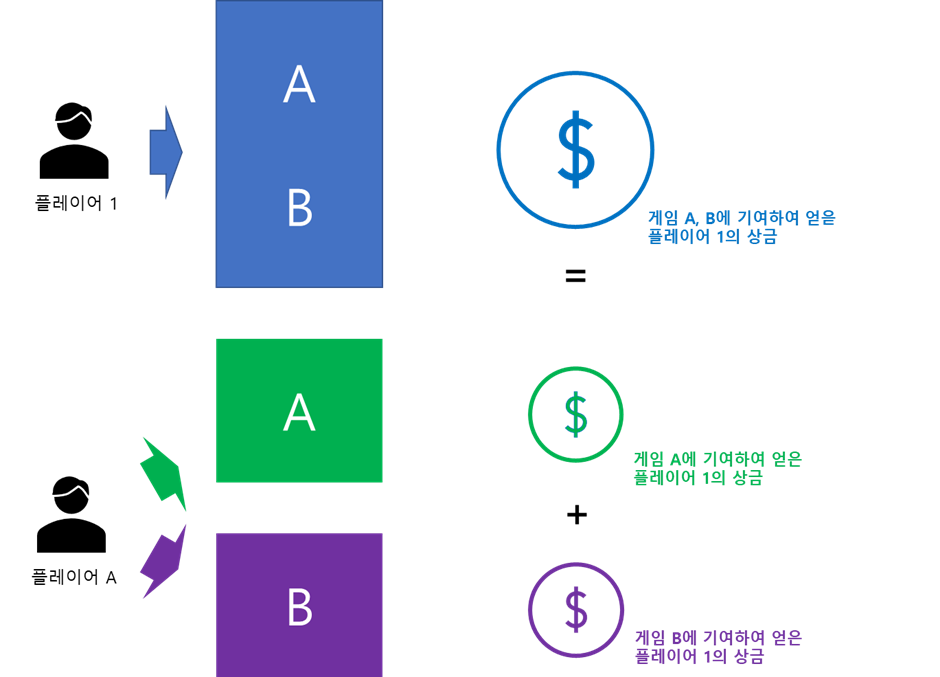
수식으로는 다음과 같다.
$ϕ_v (i)+ϕ_w (i)=ϕ_{v+w} (i)$

위의 4가지 성질을 만족하게 기여도 ϕ 를 측정한 값이 바로 Shapley Value이다. 우리는 이제 Shapley Value(기여도)를 정의해 보겠다.

위의 4가지 공리를 만족하게 기여도 $ϕ$ 를 측정한 값이 바로 Shapley Value이다.

Example

책속에 예시를 토대로 Shapley Value에 대해서 공부해보자.

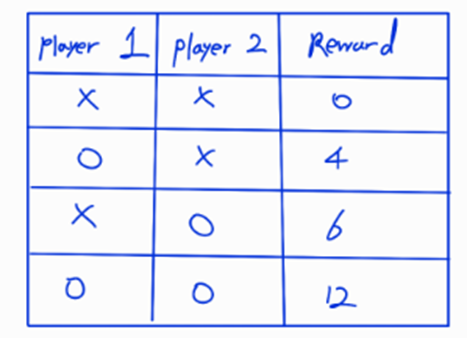
위 그림과 같이 player 1,2[ General하게는 Feature라고 생각] 할때 player가 참여하고 참여하지 않음에 따른 보상의 정도차이가 있다. 이때, 우리는 위에서 언급한 Shapley Value의 공리에 맞게 사용해서 보상을 나누어 줄 것이다.
Shaley Value의 정의는 다음과 같이 된다.

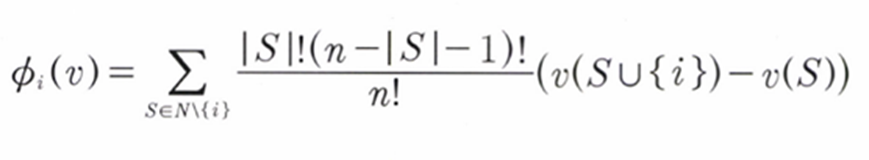
식의 뒷 부분은 i가 참여하고 참여하지 않았을 때의 Reward 차이이다[i의주변기여도] 이를 토대로 우리는 i가 미치는 기여도인 $ϕ_i$ 를 측정하는 것이 목표이다.그렇다면 player1의 기여도를 알아보자

N은 각 Featuer들의 전체 집합이다.
위의 예시를 토대로 생각해보면 {player1,player2}이다.
S는 N에서 측정하고자 하는 녀석을 제외한 부분집합들이다. 우리는 d(S)를 통해 가중평균을 계산하는데,
이때 확률을 사용한다.[확률의 합은 1이므로]
이에 대한 이해가 가는 설명이 없기 때문에 나의 의견을 쓰자면

위의
$d(s)$ 를 수정하면 위와 같은 식이 되고, 이를 해석해보면 i를 뽑고, 나머지중에 내가 선택한 S집합을 뽑을 확률이다.

SHAP (SHapley Additive exPlanation)

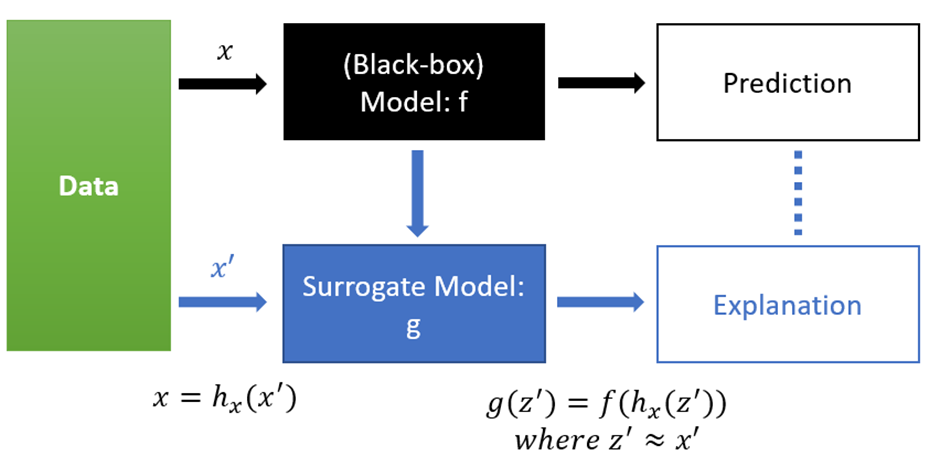
Black Box모델인 f가 있고 이를 바탕으로 한 예측이 있다. 이때, 좀 더 단순화된 입력 x’을 우리가 추정하고자 하는 모델 g에 넣음으로써, surrogate model g를 찾아 가야한다.

Definition1

Definition1> Additive Feature attribution method class
Additive Feature attribution method class는 다음을 만족하는 이진 변수에 대한 선형 Explanation model g를 갖는다.(이때, g는 유일하다는 보장이 없다)

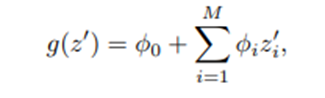
각 $z’$ 은 0 또는 1의 값을 갖고, M은 단순화된 입력 Feature의 개수이다. And $ϕ_i \in R$

논문에서는 4개의 설명 방법론이 위에서 정의한 Additive Feature attribution method에 포함된다는 것을 보인다.
e.g. LIME, DeepLIFT, Layer-Wise Relevance Propagation, Classic Shapley Value Estimation

이 논문에서는 오직 하나의 해를 갖기 위해 가져야 할 조건 3가지를 다음과 같이 제시한다

한마디로 $ϕ$ 가 Shapley Value의 경우에는 지금부터 언급할 공리들을 만족한다는 말이다.

Local accuracy

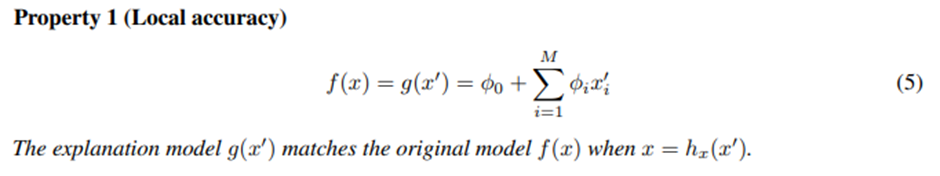
Original model f를 해석이 쉬운 모델 $g(x’)$ 을 도입해서 근사하는데, $f(x)=g(x’)$ 이면 설명력이 높아지면서 예측값과 일치되는 상황이므로 아주 이상적인 상황이다.

Missingness

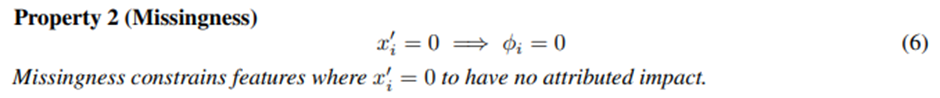
어떤 단순화 된 Feature값이 0이면 그 Feature는 기여도 또한 0이다.(If~Then)

Consistency

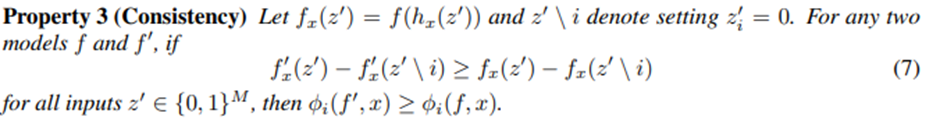
어떤 모델 f’에서 i의 영향이 f에서의 i의 영향보다 크다면 기여도 역시 마찬가지다.
(영향이 클수록 기여도도 크다)

Local accuracy : Local explanation model로 근사 가능
Missingness : Feature값이 0이면 기여도 또한 0
Consistency : i feature가 있고 없고의 차이가 더 큰 모델에서의 기여도(ϕ)가 더큼

위에 3가지 property와 정의1을 만족시킬 때, 다음과 같은 정리를 따른다.
[우리는 unique한 설명 모델 g를 결정할 수 있다.]

Theorem 1

이때, |z’|은 0이 아닌 entry의 개수이고 z’은 x’에서 0이 아닌 원소들의 집합의 부분집합이다.

NOTE
Theorem1의 방정식을 만족하는 $ϕ_i$ 가 바로 Shapley Value형태이다.
또한 Shapley value는 언급한 Axiom 1,2,3을 모두 만족한다.

이제 드디어 SHAP (SHapley Additive exPlanation) Values 을 정의해보도록 하자.

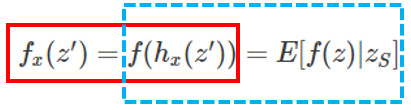
한가지 Recall해볼 사실은 SHAP values는 왼쪽 수식에서 빨간색 박스 관계를 갖고 있다는 것이다. 이때, 우리가 정의를 하는 것이 바로 하늘색 박스의 관계이다.
이때, 우리는 하늘색 점선박스의 의미를 알면 된다.
우리가 만약에 보험료를 측정해야하는 DataScientist라고 해보자. 이때 우리는 John에게 보험료가 왜 그렇게 측정됐을지 알려주어야 한다. 이때, 만약, 우리가 모델에 대한 정보를 모른다고 가정했을 때, $E[f(z)]$ 를 보험료로 측정할 수 있겠다. 이는 뭐 평균 보험료가 될수도 있고, 여러 상황이 가능할 것이다. 이를 Base로 해서 우리는 우리의 모델을 사용해서 측정한 John의 보험료를 설명하여야 한다. 그럴때 조건을 붙여가면 SHAP values만큼 보험료가 오르기도 줄어나가기도 할 것이다. 이때, 최종적으로 조건을 다 붙이면 우리는 SHAP values로 보험료의 측정 process를 설명 할 수 있다.
→ 이것이 SHAP values가 하는 일이다.

우리는 현재 선형적인 모델을 보고 있지만, 만약에 모델에 비선형성이 추가되거나, 각변수가 서로 dependent한 상황에서는 피처가 확장에 추가되는 순서가 중요하며, 가능한 모든 순서에 걸쳐 $\phi$ 값의 평균을 구하여 SHAP 값을 생성한다.

그렇지만 부분집합의 개수가 $2^n$ 이라는 시간복잡도를 갖기 때문에, SHAP value를 실제로 찾기란 어렵다는 이슈가 있다.
동영상 출처

SHAP의 근사치를 위한 방법(Kernel SHAP, Tree SHAP)

이를 위해서 저자들은 Kernel SHAP과 딥러닝 모델에 특화된 SHAP의 게산알고리즘인 Deep SHAP, 그리고 Linear SHAP등을 제안했다. 여기서는 Kernel SHAP과 Tree SHAP을 알아보겠다.

Kernel SHAP(Linear LIME + Shapley values)

→ KernelSHAP은 관측치 x에 대해서 각 특성값의 예측 기여도를 추정한다.

먼저 원활한 이해를 위해서, Notation을 정리해보자.
$x$ : 설명하고자 하는 모델 f에 들어갈 데이터 Vector
$x’$ : $x$ 를 단순화한 Vector
$z’$ : $x’$ 에서 feature의 결측치를 포함한 Vector[LIME에서 주변값]

저자들은 LIME의 Loss 방정식을 조정함으로써 surrogate model의 계수가 Shapley value가 되도록 다음과 같은 kernel을 제안하였다.

이때, $|z’|$ 이 0또는 M이 되면 $π_{x^{'}}(z^{'})$ 이 Infinite로 튀는 것을 주목해야한다. 실제로, 우리는 $|z’|$ 이 0또는 M이 되지 않도록 제약을 걸어서 이러한 상황을 피한다.
또한 여기서 Z는 학습할 데이터이다. 위의 정의한대로 g를 구하면 된다.

Kernel SHAP은 모델의 형태를 가정하지 않으므로 임의의 모델에 적용할 수 있다.(similarly LIME)

Kernel SHAP은 속도가 느리기 때문에, 많은 인스턴스에 대해 Shapley Value를 계산하려는 경우 사용할 수 없다.

Tree SHAP

Tree SHAP은 랜덤 포레스트나 기본 학습기를 의사결정나무(Decision Tree)를 사용하는 앙상블 모형의 경우 나무구조를 이용해서 좀 더 쉽게 SHAP Value를 구할 수 있도록 개발된 것이 Tree SHAP이다.
Tree SHAP은 별도의 데이터 없이 Value값을 구할 수 있는데,
Value값 $f_S (x_S)$ 을 다음과 같이 정의한다.

$E[f(x)│x_S] =(x_S가 속하는 leaf node의 score값) * (해당 노드에 속하는 데이터 비중)$

이때, 각 트리마다 위에 해당되는 값을 구해서 다 더하여서 최종값을 산출하면 된다. 그 이후 Shapley Value를 구하는 방식대로 기여도를 구하면 된다. Tree SHAP은 기존에 $2^n$ 의 시간 복잡도를 갖던 Tree기반 앙상블 모델에 한해서 $D^2$ [트리의 최대깊이]로 시간복잡도를 상식선으로 줄일 수 있다.

Tree SHAP은 조건부 평균을 Value로 사용하기 때문에, SHAP Value가 0이 아니지만 실제로 개별 에측값 계산시 사용되지 않는 경우가 있다.

논문
블로그 출처1
블로그 출처2
블로그 출처3
블로그 출처4

<참고>
1. z’ 데이터 randomly 생성 그림

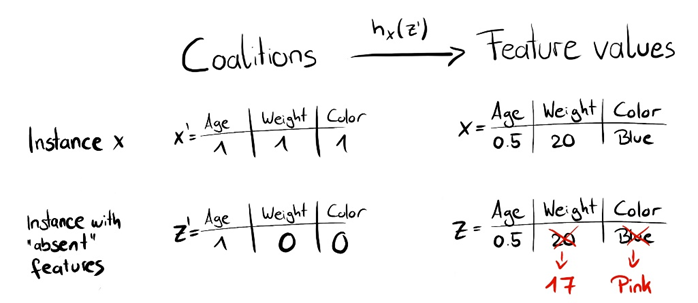
위의 그림을 설명하자면, 우리는 h_x를 원래의 Feature value로 mapping하는 map으로써 사용을 하는데, 이때 1을 갖는 값은 원래의 값으로 mapping이 되고 0을 갖는 값은 데이터의 랜덤한 특성값을 샘플링 하여 매핑 된다.

TreeSHAP 계산 방법
출처

이성준

Time-Series