퍼셉트론

: 인공신경망

• 기계학습 역사에서 가장 오래된 기계 학습 모델
• 퍼셉트론(인공두뇌학) → 다층 퍼셉트론(결합설) → 깊은 인공신경망(심층학습)

신경망 기초

인공신경망과 생물 신경망

(예시) 사람의 뉴런

두뇌의 가장 작은 정보처리 단위

• 구조
  • 세포체 - 간단한 연산
  • 수상돌기 - 신호 수신
  • 축삭 - 처리 결과를 전송

👉 뉴런을 모방한 것이 바로 "인공신경망(퍼셉트론)"

• 뉴런의 동작 이해를 모방한 초기 인공신경망 (artificial neural networks(ANN)) 연구 시작 → 퍼셉트론

• 사람의 신경망 → 인공 신경망

  • 세포체 → 노드
  • 수상돌기 → 입력
  • 축삭 → 출력
  • 시냅스 → 가중치

신경망 종류

• 전방(forward) 신경망, 순환(recurrent) 신경망

• 얕은(shallow) 신경망, 깊은(deep) 신경망

• 결정론(deterministic) 신경망

  • 모델의 매개변수와 조건에 의해 출력이 완전히 결정되는 신경망

• 확률론적(stochastic) 신경망

  • 고유의 임의성을 가지고 매개변수와 조건이 같더라도 다른 출력을 가지는 신경망

💡 신경망의 구조에 따라 다양한 형태의 신경망이 존재

퍼셉트론

• 원시적 신경망으로써 깊은 인공신경망을 포함한 현대 인공신경망의 토대
  • 깊은 인공신경망은 퍼셉트론의 병렬 배치를 순차적 구조로 결합한 형태
• 구조
  • 절(node)
  • 가중치(weight)
  • 층(layer)

퍼셉트론 구조

• 입력
  • $i$번째 노드는 특정 벡터 $\bold x$ 의 요소 $x_i$를 담당
  • 항상 1이 입력되는 편향 노드 포함
• 입력과 출력 사이의 연산
  • $i$번째 입력 노드와 출력 노드를 연결하는 변은 가중치 $w_i$를 가짐 (퍼셉트론은 단일 층 구조 라고 간주)
• 출력
  • $i$번째 노드에 의해 수치(+1 or -1) 출력

퍼셉트론 동작

• 선형 연산 → 비선형 연산

  1. 선형 연산 : 입력(특징)값과 가중치를 곱하고 모두 더해 $s$를 구함
  2. 비선형 연산 : 활성함수 $\tau(s)$를 적용
     • 활성함수로 계단 함수 사용 (출력 y=1 or y=-1)

• 행렬 표기

  1. $s=\bold w^T\bold x+w_0$
     • $\bold x=(x_1, x_2,\cdots,x_d)^T, \bold w=(w_1,w_2,\cdots,w_d)^T$
  2. $s=\bold w^T\bold x$ (편향 항 $w_0$을 벡터에 추가)
     • $\bold x=(1,x_1, x_2,\cdots,x_d)^T, \bold w=(w_0,w_1,w_2,\cdots,w_d)^T$
  • 퍼셉트론의 동작은 $y=\tau(\bold w^T\bold x)$

• 결정 직선

  • $d(\bold x) = d(x_1,x_2)=w_1x_1+w_2x_2+w_0=0$
  • $w_1$과 $w_2$는 직선의 기울기, $w_0$은 절편(편향)을 결정
  • 여기서 결정 직선은 특징 공간을 (예)+1,-1 의 두 부분공간으로 이분할하는 분류기 역할

• $d$ 차원 공간으로 일반화

  • $d(\bold x)=w_1x_1+\cdots+w_dx_d+w_0=0$
    • 2차원: 결정 직선
    • 3차원: 결정 평면
    • 4차원 이상: 결정 초평면

학습

• $w_0, w_1, w_2$ 가중치 값은 어떤 값을 가져야 할지?

• 일반적인 분류기의 학습 과정

  1. 과업 정의, 분류 과정의 수학적 정의(가설 설정)
  2. 해당 분류기의 목적함수 $J(\Theta)$ 정의
  3. $J(\Theta)$를 최소화하는 $\Theta$ 를 찾기 위한 최적화 수행

1. 단계: 목적함수 정의 (가설 - 퍼셉트론)

   • 매개변수 집합 : $\Theta=\{\bold w\}$
   • 목적함수 : $J(\Theta)=J(\bold w)$
   • ⭐ 퍼셉트론 목적함수의 상세 조건
     1. $J(\bold w)\ge0$
     2. 모든 샘플을 맞히면 $J(\bold w)=0$
     3. 틀리는 샘플이 많은 $\bold w$일수록 $J(\bold w)$는 큰 값을 가짐

2. 단계: 목적함수 상세 설계

   $J(\bold w)=\sum_{x_k\in Y}-y_k(\bold w^T\bold x_k)$
   • ($Y$는 틀리는 샘플의 집합)
   • 위의 식은 퍼셉트론 목적함수의 상세 조건을 만족하므로 퍼센트론의 목적함수로 적합!
     1. $-y_k(\bold w^T\bold x_k)$ 는 항상 양수를 가짐 👉 만족
        • 임의의 샘플 $x_k$ 가 $Y$에 속한다면,
          퍼셉트론의 예측값 $\bold w^T\bold x_k$ 와 실제값 $y_k$ 의 부호는 다름 → (+1, -1 or -1,+1)
     2. $Y$가 클수록 (틀린 샘플이 많을수록)
        $J(\bold w)$는 큰 값을 가짐 👉 만족
     3. $Y$가 공집합일 때 (모든 샘플을 맞출 때)
        $J(\bold w)=0$ 👉 만족

3. 단계: ⭐ 경사 하강법 (gradient descent)

   • 목적함수 $J(\Theta)$의 기울기를 이용하여 최소값을 가지는 극값을 찾음
   • 경사도 계산
     • 일반화된 가중치 갱신 규칙 $\Theta=\Theta-p\bold g$ 를 적용
       (경사도 $\bold g$ (gradient) 필요)
     • 편미분을 이용
   • 델타규칙(delta rule)
   • 학습률(learning rate) 에 따라 반복 탐색

💡 학습률을 너무 작게 또는 너무 크지 않게 적절하게 지정해주는 것이 중요하다 (너무 크거나 작으면 반복 횟수가 많아짐)

• 퍼셉트론 학습 알고리즘 (완벽하게 양분화 된다고 가정)

  

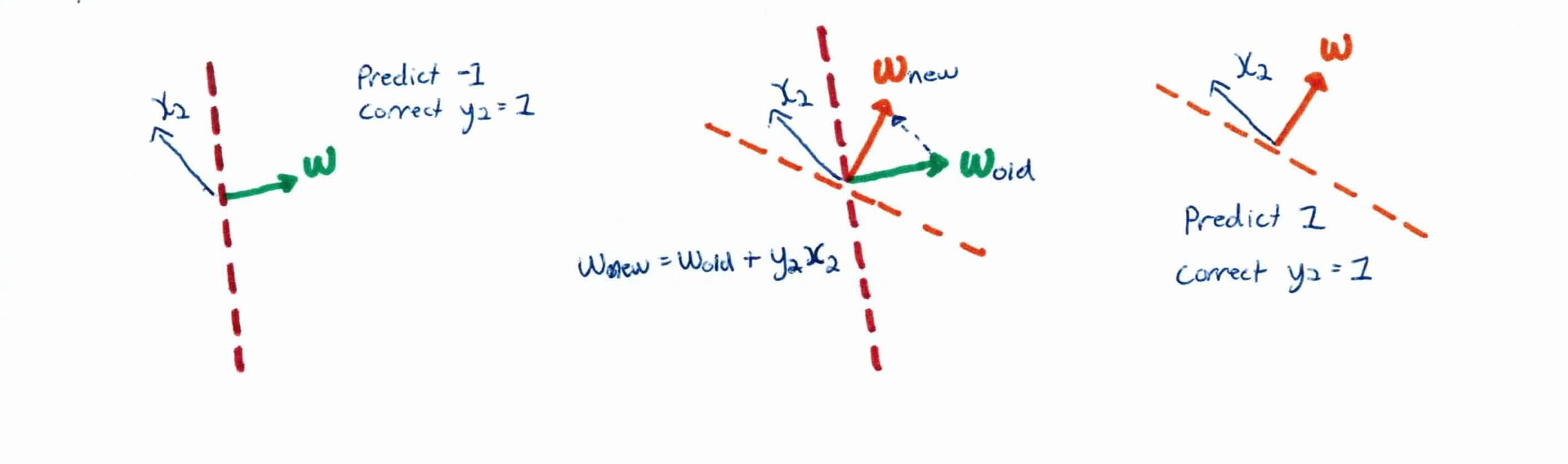
  출처: https://kseow.com/perceptron.html

  • 확률론적(stochastic) 형태
    • 샘플 순서를 섞고, 틀린 샘플이 발생하면 즉시 갱신
  • 무리(batch) 형태
    • 훈련집합의 샘플을 모두 맞출 때가지 세대(epoch)를 반복

💡 선형분리가 불가능한 경우

• 퍼셉트론 적용하지 않는 것이 일반적
• 다층 퍼셉트론을 이용