심층학습 기초

컨볼루션 신경망

컨볼루션 (합성곱) 신경망 (CNN, Convolution Neural Network)

• 컴퓨터 비전의 어려운 점
  • 시점의 변화
    • 동일한 객체라도 영상을 찍는 카메라의 각도나 이동에 따라 모든 픽셀값이 변화됨
  • 경계색(보호색)으로 배경과 구분이 어려운 경우
  • 조명에 따른 변화
  • 기형적인 형태의 영상 존재
    • 일반적인 형태와 다른 형태
  • 일부가 가려진 형태
  • 같은 종류 간의 변화가 큼

💡 컨볼루션 신경망은 영상 인식에 특화되어 있음!

• 구조

  • 컨볼루션층 (CONV)
    • 선형함수인 컨볼루션과 비선형 함수인 활성함수의 조합
  • 풀링층 (POOL)
    • 컨볼루션의 얻어진 특징을 통계적으로 압축

• DMLP vs CNN

  • DMLP
    • 완전 연결(FC) 구조로 높은 복잡도
    • 학습이 매우 느리고 과잉적합 우려
  • CNN
    • 컨볼루션 연산을 이용한 부분연결(희소 연결) 구조로 복잡도 크게 낮춤
    • 컨볼루션 연산은 좋은 특징 추출

👉 CNN은 부분 연결 구조

• CONV : 학습에 의해 결정된 복수의 필터들(커널들)에 대응되는 특징들을 추출하는 층

  • 각 층의 입출력의 특징형상 유지 (특징맵)
  • 영상의 공간 정보를 유지하면서 공간적으로 인접한 정보의 특징을 효과적으로 인식
  • 각 필터(커널)는 파라미터를 공유함으로써 완전 연결 신경망 대비 학습 파라미터가 매우 적음

• POOL : 추출된 영상의 특징을 요약하고 강화하는 층

• CNN 특징

  • 격자(grid) 구조를 갖는 데이터에 적합
    • 영상, 음성 등
  • 수용장(receptive field)은 인간의 시각과 유사
  • 가변 크기의 입력 처리 가능

📌 컨볼루션 신경망 예제 🔗

신경망의 구조가 어떠한 형태로 배치되어 있는지 파악에 용이

컨볼루션층 (CONV)

• 컨볼루션(convolution) (합성곱) 연산
  • 해당하는 요소끼리 곱하고 결과를 모두 더하는 선형 연산
  • 입력 $\circledast$ 커널(필터) → 출력(특징 맵) 으로 구성됨

👉 영상에서 특징을 추출하기 위한 용도로 사용됨 (=공간 필터 (spatial filtering))

• 컨볼루션 연산의 예

  

  사진출처: http://wiki.hash.kr/index.php?title=합성곱_신경망&mobileaction=toggle_view_desktop

• 3차원 (혹은 채널 channel) 컨볼루션 연산의 예

  

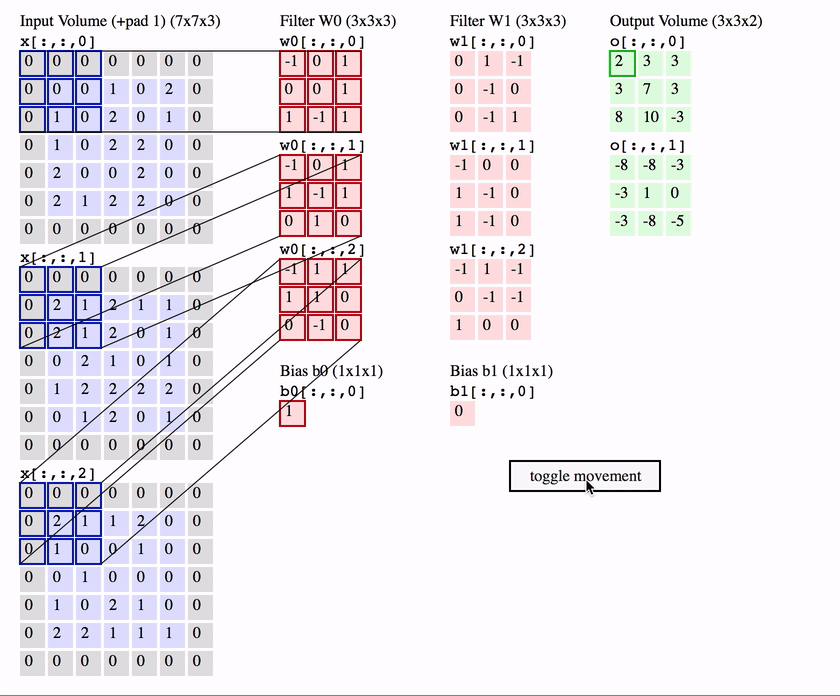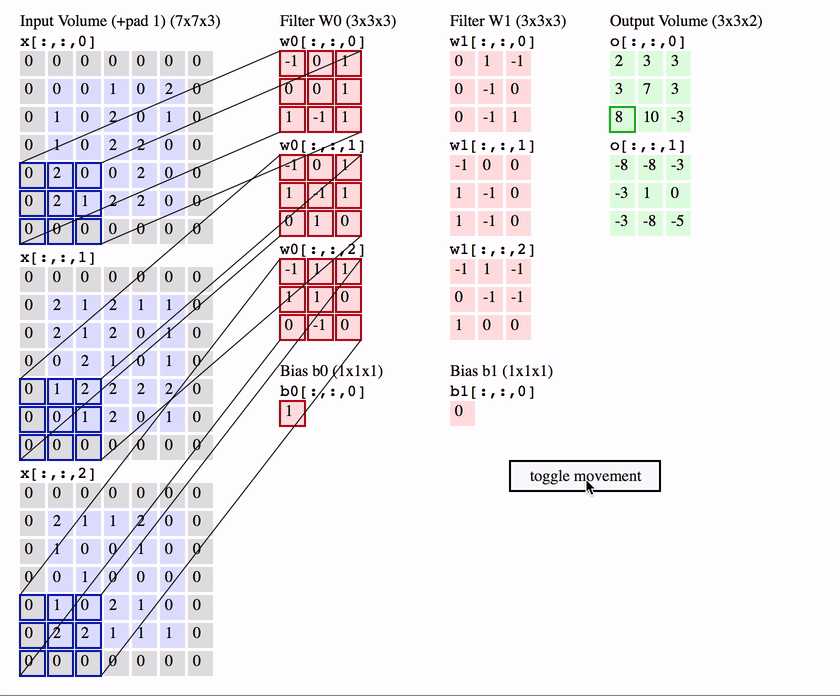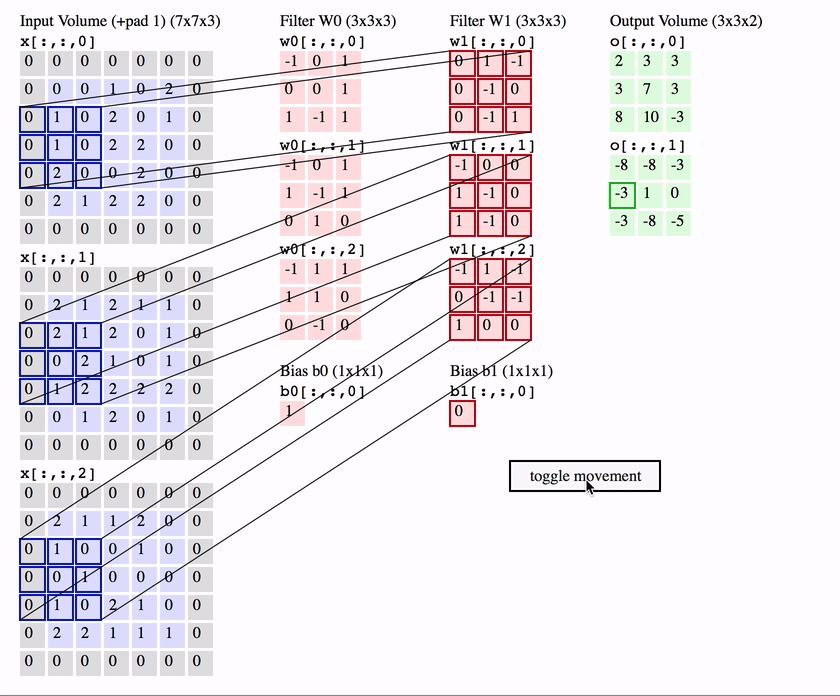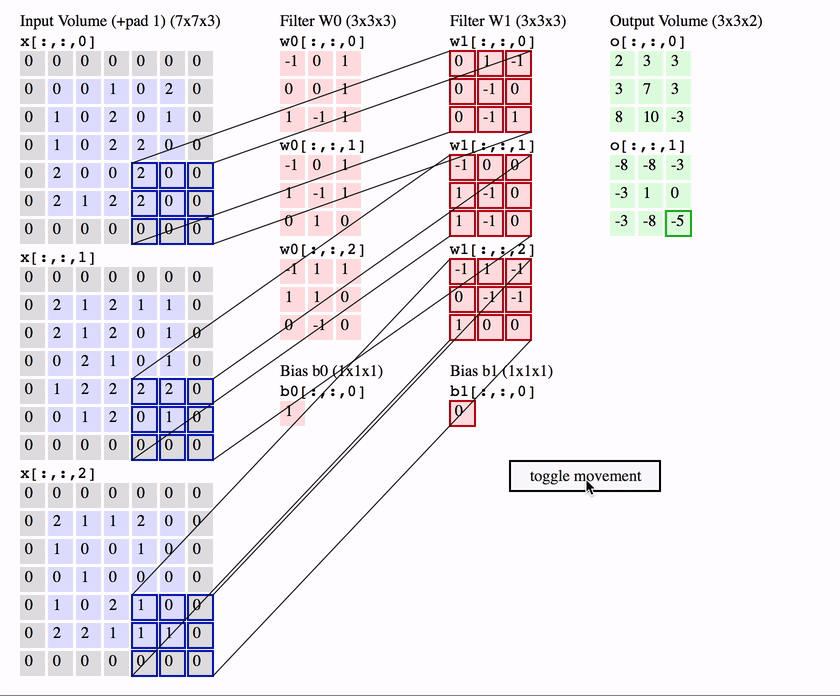
  사진출처: https://medium.com/@seoilgun/cnn의-stationarity와-locality-610166700979

💡 필터는 학습에 의해 결정됨 → 특징 학습

• padding(덧대기)

  • 가장자리에서 영상의 크기가 줄어드는 효과 방지 (각 층의 입출력의 특징형상 유지)
  • 보통 0으로 채움

• bias(편향 추가)

• weight sharing(가중치 공유)

  • 모든 노드가 동일한 커널을 사용
  • 모델의 복잡도가 크게 낮아짐

• 다중 특징 맵 추출

  • 커널의 값에 따라 커널이 추출하는 특징이 달라짐
  • 하나의 커널만 사용하면 빈약한 특징이 추출됨

👉 하나의 입력에 여러 개의 커널을 사용

• 특징 학습
  • 커널을 사람이 설계하지 않고, 학습으로 찾음

👉 DMLP와 마찬가지로 오류 역전파로 커널을 학습

• 컨볼루션 연산에 따른 CNN 의 특성
  • 이동에 동변
    • 신호가 이동하면 이동 정보가 그대로 특징 맵에 반영 → 영상 인식에서 물체 이동이나 음성 인식에서 발음 지연에 효과적으로 대처
  • 병렬분산 구조
    • 각 노드는 독립적으로 계산 가능한 병렬 구조
    • 노드는 깊은 층을 거치면서 전체에 영향을 미치므로 분산 구조
• 큰 보폭(stride)에 의한 다운샘플링(down-sampling)
  • 보폭이 $k$이면, $k$개 마다 하나씩 샘플링하여 커널 적용
• 텐서 적용
  • 3차원 이상의 구조에도 적용 가능
• 3차원 구조의 데이터 적용
  • 채널이 $k$개인 3차원 격자 구조

💡 커널의 개수 == 특징 맵의 개수

풀링층 (POOL)

• 풀링 연산
  • 특징 맵을 다운샘플링하여 특성 맵의 크기를 줄이는 연산
  • 최대 풀링, 평균 풀링, 가중치 평균 풀링 등
• 풀링 연산의 특징
  • 풀링은 상세 내용에서 요약 혹은 평균 등의 대표성을 추출함
  • 매개변수가 없음
  • 특징 맵의 수를 그대로 유지함

전체 구조

• 빌딩 블록(building block)

  • CNN은 빌딩 블록을 이어 붙여 깊은 구조로 확장

  • 일반적인 빌딩블록: 컨볼루션층 → 활성함수 (주로 ReLU) → 풀링층

    ![https://velog.velcdn.com/images%2Fleeyongjoo%2Fpost%2Fe65c64fb-4beb-42c6-af38-926e9a7cb59b%2Fimage.png%5D(https%3A%2F%2Fimages.velog.io%2Fimages%2Fleeyongjoo%2Fpost%2Fe65c64fb-4beb-42c6-af38-926e9a7cb59b%2Fimage.png)

    사진출처: https://subeans.tistory.com/26

• 컨볼루션 층의 출력 크기와 매개변수 수

  • 입력 : W1 H1 D1, 커널: K개 F*F, 보폭: S, 패딩: P
    • (일반적으로 F=2,S-2 혹은 F=3,S=1 사용)
  • 출력의 크기: W2 H2 D2
    • W2 = (W1 - F + 2P) / S + 1
    • H2 = (H1 - F + 2P) / S + 1
    • D2 = K
  • 매개변수의 수:
    • 커널마다 (FF D1)개의 가중치와 1개의 바이어스를 가짐
    • 따라서, 전체 매개변수의 수는 (FF D1)K + K
  • (예제)
    • 입력크기 : 32323
    • 10개의 5*5 커널, 보폭 1, 패딩 2
    • 출력 크기 : (32+22-5)/1 + 1 = 32 → 3232*10
    • 매개변수 수 : 553 + 1 = 76(+1은 편향) → 76*10 = 760

📌 초창기 CNN 사례 : LeNet-5

• 특징 추출: CONV-POOL-CONV-POOL-CONV의 다섯층을 통해 28*28 명암 영상을 120차원의 특징 벡터로 변환 (평균 풀링 사용)
• 분류: 은닉층이 하나인 MLP

👉 CNN의 첫 번째 성공사례: 필기 숫자 인식기를 만들어 수표 인식 자동화 시스템 구현

📌 CNN 시각화 예제 🔗

📃 참고하면 좋은 자료

PyTorch로 시작하는 딥 러닝 입문 - 합성곱과 풀링