Kinematic Model

정승균·2021년 2월 1일
0

자율주행 제어

목록 보기
1/8
post-thumbnail
  • Kinematic Model : Force나 Torque를 고려하지 않는 모델 (운동 방정식 X)

Ⅰ. 좌표계

1. World Coordinate System

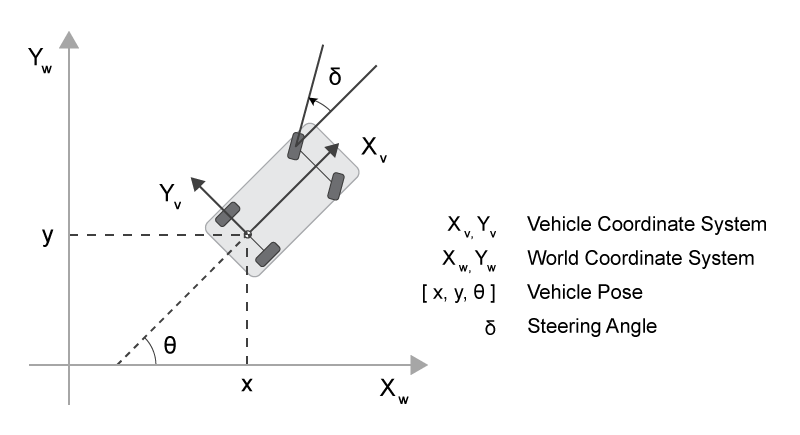
2. Vehicle coordinate system


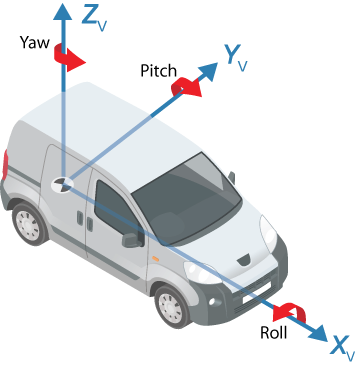
Ⅱ.Kinematic bicycle model

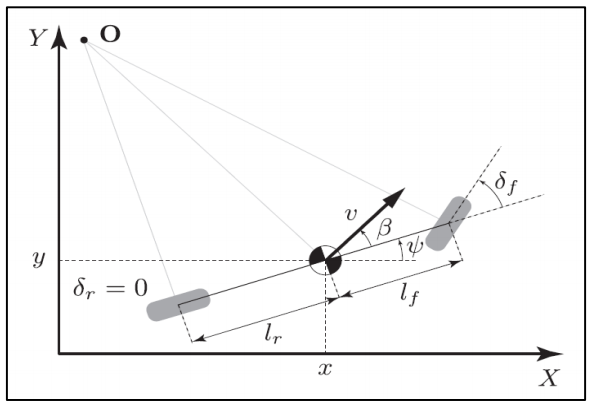
1. rear wheel reference point

Assumptions :

  1. No tire slip
  2. 0 steer angle at rear wheel
  • 뒷바퀴와 앞바퀴 속도 벡터 XY 축 분해
VRX=VRcos⁡ψ...(1)VRY=VRsin⁡ψ...(2)VFX=VFcos⁡(δ+ψ)...(3)VFY=VFsin⁡(δ+ψ)...(4)V_{RX} = V_R\cos{\psi}\quad...(1)\\ V_{RY} = V_R\sin{\psi}\quad...(2)\\ V_{FX} = V_F\cos({\delta + \psi})\quad...(3)\\ V_{FY} = V_F\sin({\delta + \psi})\quad...(4)\\
  • 직각삼각형에서
sin⁡ψ=ΔYL...(5)cos⁡ψ=ΔXL...(6)\sin{\psi} = \frac{\Delta Y}{L}\quad...(5)\\ {}\\ \cos{\psi} = \frac{\Delta X}{L}\quad...(6)
  • (5), (6) 시간에 대하여 미분
ψ˙cos⁡ψ=VFY−VRYL...(7)−ψ˙sin⁡ψ=VFX−VRXL...(8)\dot{\psi}\cos{\psi} = \frac{V_{FY}-V_{RY}}{L}\quad...(7)\\ -\dot{\psi}\sin{\psi} = \frac{V_{FX}-V_{RX}}{L}\quad...(8)\\
  • (7), (8) 에 (1)~(4) 대입
ψ˙cos⁡ψ=VFsin⁡(δ+ψ)−VRsin⁡ψL...(9)−ψ˙sin⁡ψ=VFcos⁡(δ+ψ)−VRcos⁡ψL...(10)\dot{\psi}\cos{\psi} = \frac{V_F\sin({\delta + \psi})-V_R\sin{\psi}}{L}\quad...(9)\\ {}\\ -\dot{\psi}\sin{\psi} = \frac{V_F\cos(\delta+\psi)-V_R\cos\psi}{L}\quad...(10)\\

  • (9), (10) 을 연립하여 V_F 소거하여 정리하면
Lψ˙(  cos⁡(δ+ψ)cos⁡ψ+sin⁡(δ+ψ)sin⁡ψ  )=VR(sin⁡(δ+ψ)cos⁡ψ)−cos⁡(δ+ψ)sin⁡ψ)L\dot{\psi}(\;\cos(\delta+\psi)\cos{\psi} + \sin(\delta+\psi)\sin{\psi}\;) = V_R(\sin(\delta+\psi)\cos\psi) - \cos(\delta+\psi)\sin\psi)

  • 삼각함수 공식에 의해
Lψ˙cos⁡δ=VRsin⁡δ∴  ψ˙=VRtan⁡δL...(11)L\dot{\psi}\cos\delta = V_R\sin\delta\\ {}\\ \therefore\; \dot{\psi} = \frac{V_R\tan{\delta}}{L} \quad ...(11)
  • 따라서 (1), (2), (11)를 rear wheel 에 대해 서술하면,
X˙=Vcos⁡ψY˙=Vsin⁡ψψ˙=Vtan⁡δL\dot{X} = V\cos{\psi}\\ \dot{Y} = V\sin{\psi}\\ \dot{\psi} = \frac{V\tan{\delta}}{L}

2. center of gravity reference point

  • 비슷한 방식으로 유도 가능
ψ˙=vR=vcos⁡βtan⁡δLx˙=vsin⁡(ψ+β)y˙=vcos⁡(ψ+β)\dot {\psi} = \frac{v}{R} = \frac{v\cos{\beta}\tan{\delta}}{L} \\ {}\\ \dot{x} = v \sin{(\psi+\beta)}\\ \dot{y} = v \cos{(\psi+\beta)}

Ⅲ. 파이썬 코드 구현

class VehicleModel(object):
    L = 0.5
    def __init__(self, x=0.0, y=0.0, yaw=0.0, v=0.0):
        self.x = x
        self.y = y
        self.yaw = yaw
        self.v = v

        self.max_steering = np.radians(30)

    def update(self, steer, a=0):
        steer = np.clip(steer, -self.max_steering, self.max_steering)
        self.x += self.v * np.cos(self.yaw) * dt
        self.y += self.v * np.sin(self.yaw) * dt
        self.yaw += self.v / self.L * np.tan(steer) * dt
        self.yaw = self.yaw % (2.0 * np.pi)
        self.v += a * dt

profile
정승균
다음 포스트

Dynamic Model

0개의 댓글