- 공기저항, road friction, slip 등을 고려하여 Kinematic 모델보다 높은 fidelity를 갖음
tire model
- tire slip angle이 5도 이내에서는 선형적으로 근사 가능
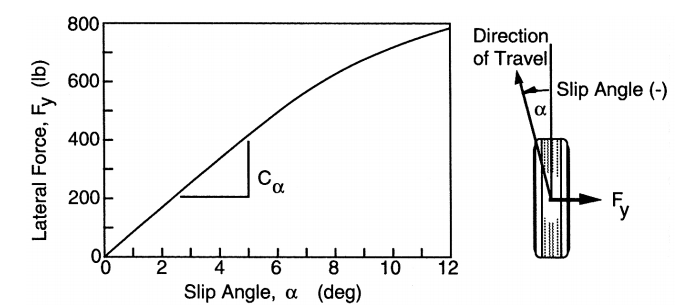
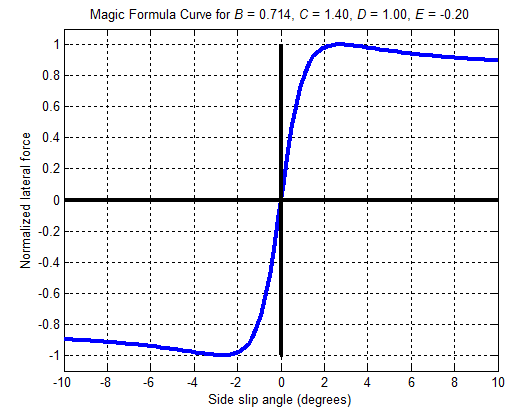
- 레이싱카 같은 slip angle의 범위가 넓은 경우 Pacejka tire model를 씀
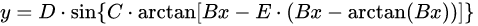
Ⅰ. lateral dynamics
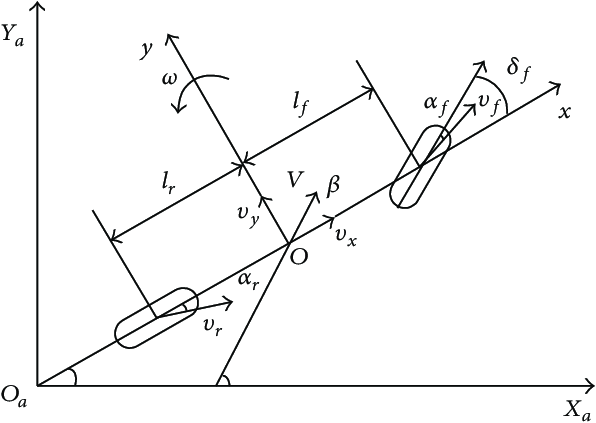
Assumptions :
- small steer angle at front wheel
- 0 steer angle at rear wheel
- v_x is constant
- linear tire model
- Front Wheel 의 속도 xy좌표로 계산
- Rear Wheel 의 속도 xy좌표로 계산
- (1), (2)의 x축 y축 속도와 slip angle의 정의에 의해서
- 작은 각도로 가정하였으므로
- linear tire model와 (3), (4)에 의해 (5도 이내의 tire slip angle)
- y 축 가속도 계산
- Translation 운동 방정식과 (5), (6), (7) 에 의해서
- 이 식을 정리하면
- Rotation 운동 방정식과 (5), (6) 에 의해서
- 이 식을 정리하면
- (8), (9)를 이용한 state-space-representation
Ⅲ. longitudinal dynamics
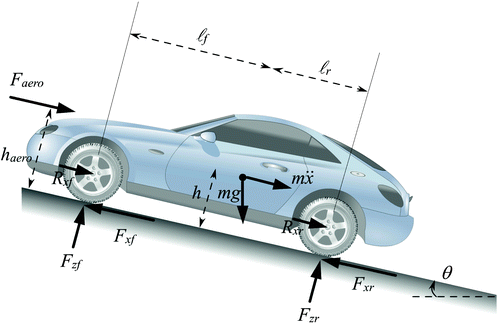
1. 공기저항
2. 구름저항
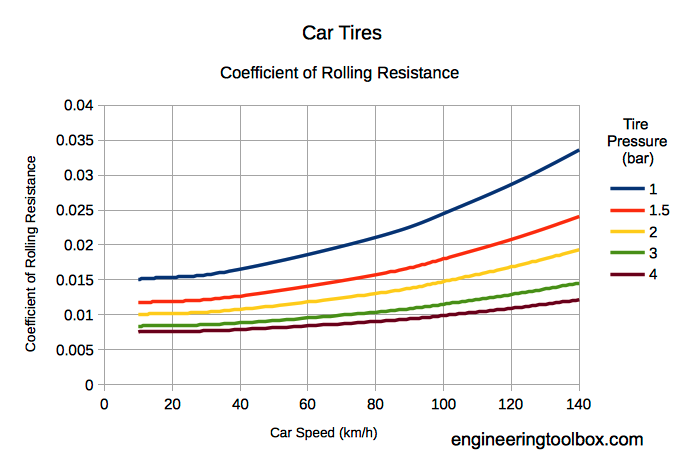
- ( 은 공기압과 차량속도에 의해 결정됨)
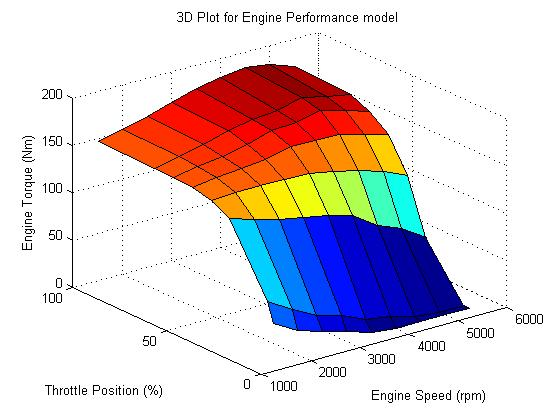
3. Powertrain
- 수식으로 표현하기 복잡하므로 3d plot을 사용함