Path finding Algorithm

정승균·2021년 2월 6일
0

자율주행 제어

목록 보기
8/8
post-thumbnail

Ⅰ. Dijkstra Algorithm

1. Cost 설정

  • cost = g(s) : 시작노드에서부터 노드 s 까지의 최소 cost
    g(s)=min⁡s′∈visited(g(s′)+c(s′,  s))g(s) = \min_{s' \in visited}({g(s')+c(s',\;s)})

2. 알고리즘

  1. Open = {start_node}, Close= { }
  2. Open에서 cost가 가장 낮은 노드를 탐색하여 curr_node에 지정
  3. curr_node 가 goal_node와 같으면 종료
  4. curr_node 가 goal_node가 아니면
    a. Open에서 curr_node 제거
    b. Closed에 curr_node 추가
    c. curr_node에서 갈 수 있는 neighbor 노드 검색
    d. neighbor가 Closed에 있으면 다음 neighbor 검색
    e. neighbor가 Open에 있으면 cost 업데이트
    g(sneig)=min⁡(  g(sneig),  g(scurr)+c(ncurr,  nneig))g(s_{neig}) = \min (\; g(s_{neig}), \; g(s_{curr}) + c(n_{curr}, \; n_{neig}) )
    f. neighbor가 Open에 없으면 Open에 추가
  5. 2~4 반복

2. 예시


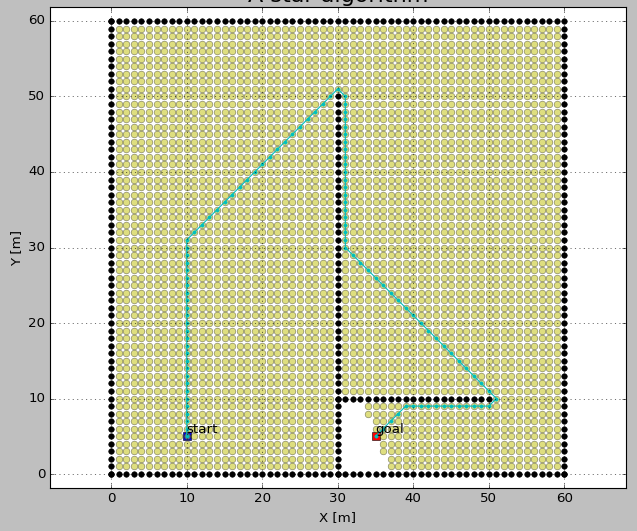
Ⅱ. A* Algorithm

1. cost 설정

  • Dijkstra의 넓은 탐색범위를 좁혀주기 위해 cost함수로 g(s)+ w*h(s) 사용
  • h(s) 는 보통 Euclidian distance로 사용

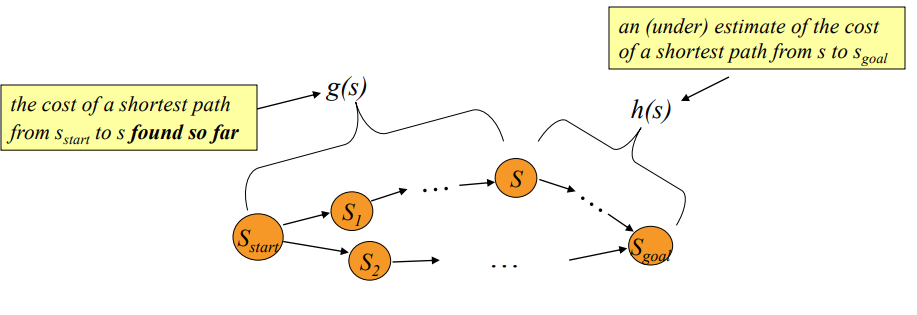
2. 예시

  • Dijkstra의 탐색 범위보다 적어진 대신 경로 거리는 늘어난 것을 볼 수 있다


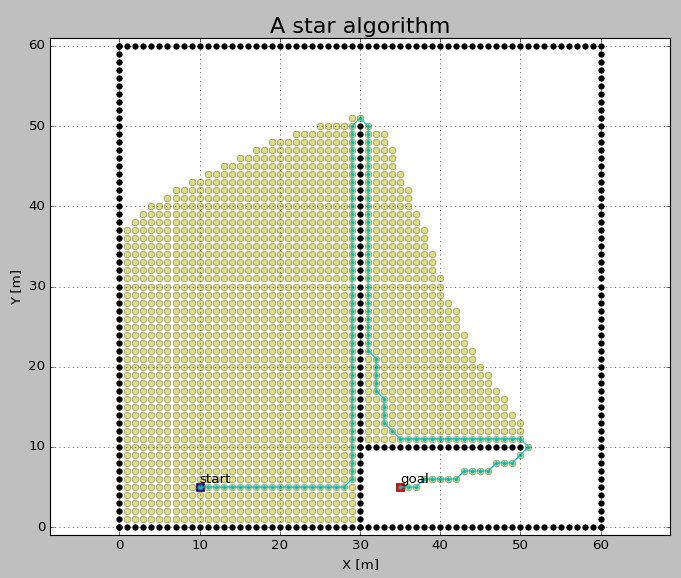
Ⅲ. Hybrid A* Algorithm

  • A* 알고리즘의 discrete함을 보완한 알고리즘 -> continuous한 state로 expand
  • 차량 주행 경로에 더 적절함


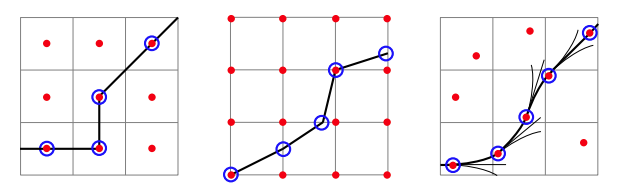
Ⅳ. RRT Algorithm

  • Rapidly exploring Random Tree

1. 알고리즘

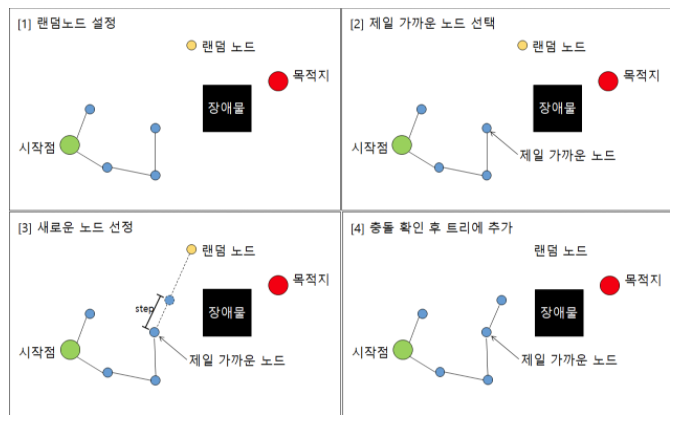
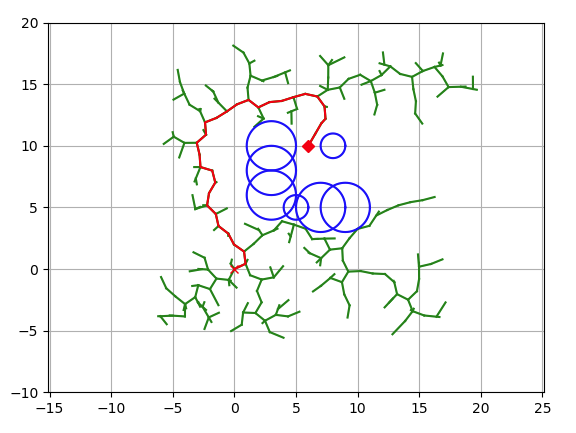
2. 예시


Ⅳ. RRT* Algorithm

  • 트리를 구성하는 노드를 대체하여 비용을 줄일 수 있으면 기존 노드를 대체하여 트리를 구성

1. 알고리즘

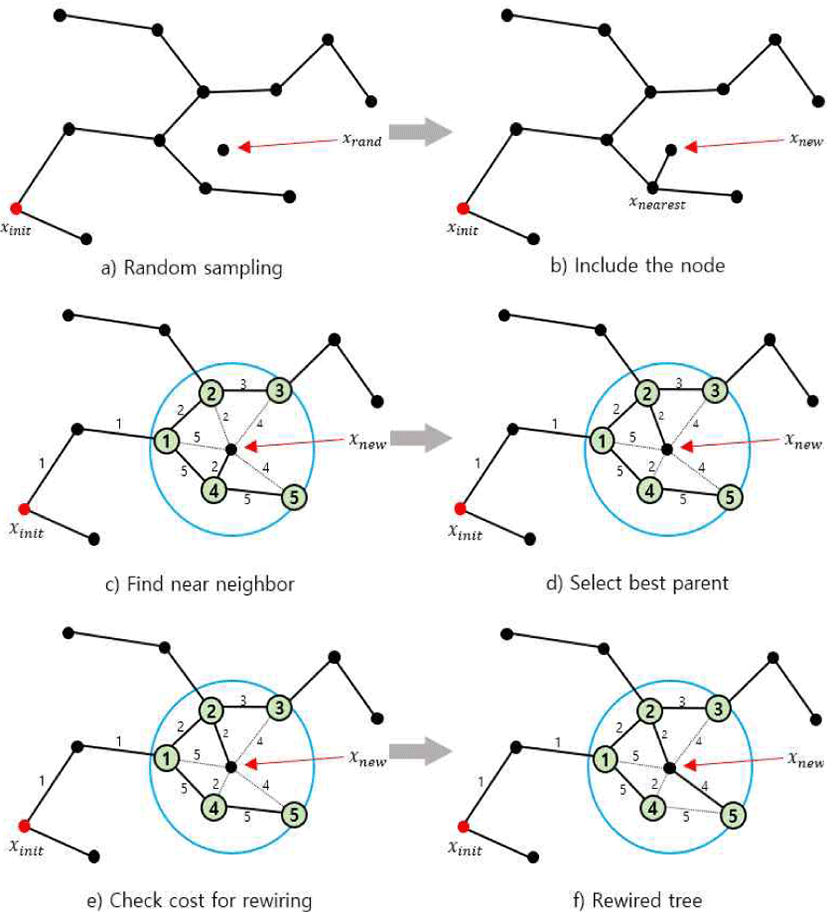
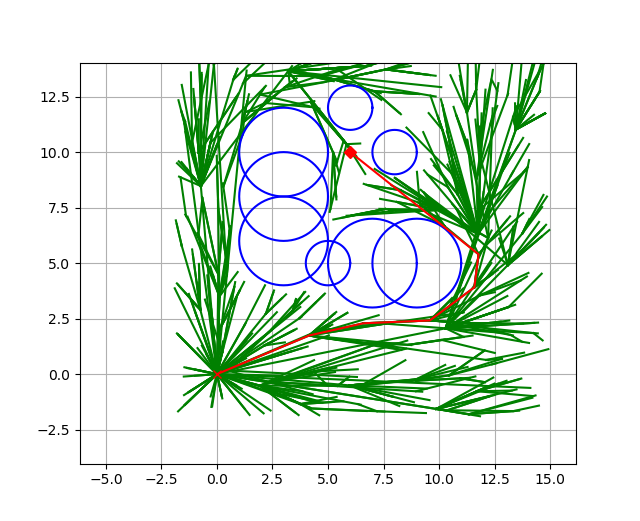
2. 예시

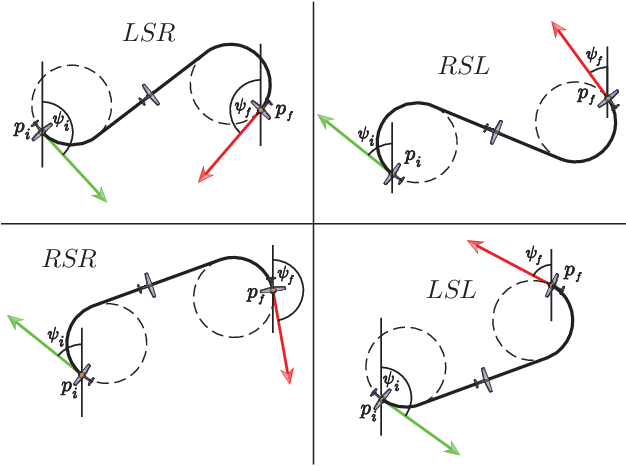
3. Dubins / CCRS

  • RRT*의 node를 extend할때 사용할 수 있음

  • 두 노드를 잇는 곡선 경로를 계산

  • Continuous Curvature Reeds-Sheep


Ⅴ. Informed RRT* Algorithm

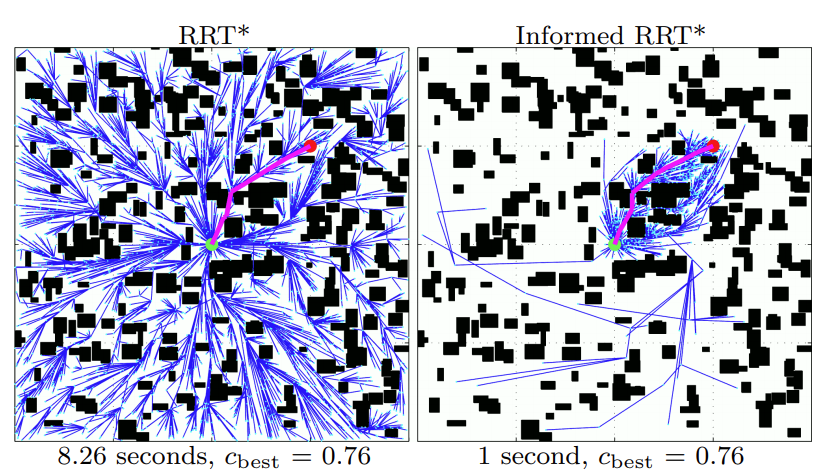
  • Searching area를 제한해서 planning 효율성을 높임

1. 알고리즘

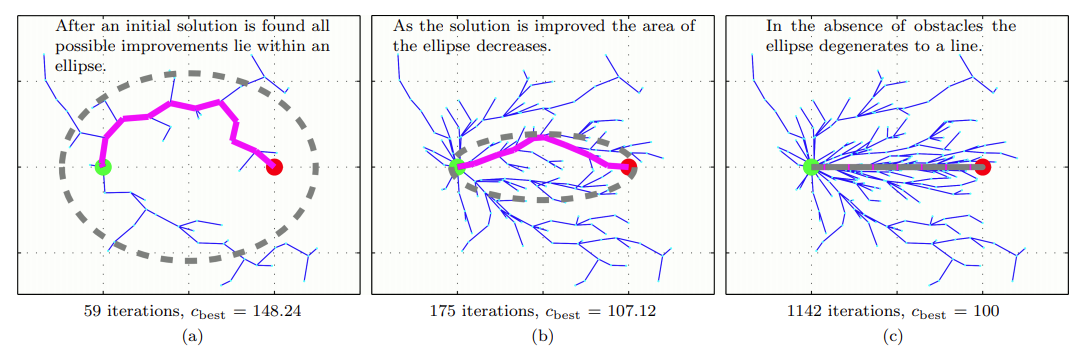
  1. initial solution을 구함
  2. solution의 길이를 장축으로 하고 start와 goal를 초점으로 하는 타원 생성
  3. 타원의 특성상 더 나은 solution은 타원 내부에서만 존재
  4. 타원 내에서 sampling을 진행해서 더 optimal한 solution 탐색

2. 비교



profile
정승균
이전 포스트

Optimal Frenet planning algorithm

0개의 댓글