1. Frenet Frame
- 좌측이 Cartesian Frame, 우측이 Frenet Frame
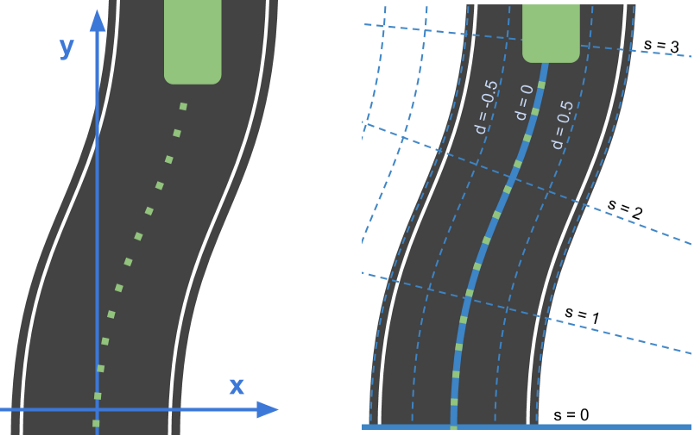
2. Polynomial Trajectory Generation
-
Frenet Frame상에서 polynomial path를 생성
-
횡방향 : initial value 와 target value 와 target time 로 5차 다항식 계산
-
종방향 : initial value 와 target value 와 target time 로 4차 다항식 계산
3. Trajectory Check
- 속도 제한 체크
- 가속도 제한 체크
- curvature 제한 체크
- collision 체크 : Euclidean distance-based check
4. Optimal trajectory selection
-
종방향 Cost
- longitudinal jerk : 종 방향 안정감
- veltocity deviation : 타켓 속도와 얼마나 근접하였는지
- time interval : 얼마나 빨리 조건에 도달하였는지
-
횡방향 Cost
- lateral jerk : 횡 방향 안정감
- time interval : 얼마나 빨리 조건에 도달하였는지
- terminal lateral deviation : 이전 optimal 경로와의 변화, 경로 떨림 방짐
-
Total Cost
