오답이나 추가 이해 풀이하는 공간
Linked List의 시간 복잡도를 Big-O 표기법으로 나타낸 것 중 틀린 것은?
A Search - O(n)
B Insert - O(n)
C Access - O(1)
D Deletion - O(n)
B는 O(1)라고 적혀있던 걸로 기억해서 선택했는데 틀렸다. 유어클래스 내용이라서 선택했는뎃!ㅎㅎ;
체크포인트에서의 포인트!
일반적인 경우는 삽입과 삭제할 때, 위치가 특정되어지지 않았을 경우, O(n)이 맞다!
C
두 알고리즘 A, B의 시간 복잡도가 각각 O(n), O(logn) 라면, 알고리즘 B가 알고리즘 A 보다 항상 빠르다.
O(log n)은 후반부로 갈수록 시간이 증가하기 때문에 항상 빠르지 않으므로 '거짓'이 된다. 입력값이 특정되어지지 않고, 클 경우 얼마든지 다르게 있다.
입력값이 작을 때는 굳이 저 두 개를 비교할 필요는 없다.
거짓
다음의 시간 복잡도를 가지는 알고리즘들이 있을 때, 가장 느린 것과 가장 빠른 것을 모두 고르면? (단, n ≥ 10,000)
A O(n log n)
B O(2n)
C O(log n)
D O(n2)
E O(n!)
위 보기에서 가장 빠른 것으로는 log n이라고 생각해서 선택했고, 가장 느린 것은 n! 으로 선택했다. 조금 긴가민가했는데 그래프 재확인하니 확실히 맞았다.
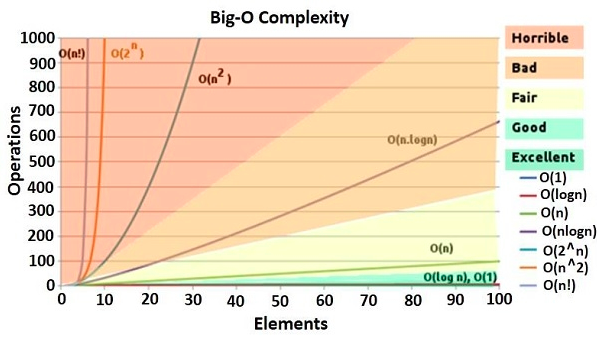
C,E
다음과 같은 코드의 시간 복잡도로 올바른 것은?
for (let i=0; i<n; i++) {
for (let j=0; j<i; j++) {
// do something
}
}A O(n)
B O(n (n-1) / 2)
C O(n (n + 1) / 2)
D O(n2)
E O(log n)
- 연산횟수를 따지면 (n*(n-1)/2) 인데, 빅오 표기법으로 따지면 D이다.
- 상수는 무시한다.
D
다음과 같은 코드의 시간 복잡도를 올바르게 나타낸 것은?
let i = N;
while (parseInt(i > 0)) {
i = i / 2;
}
A O(n)
B O(log n)
C O(n log n)
D O(n2)
//원래 문제출제 의도
let i = N;
while (parseInt(i) > 0) {
i = i / 2;
}
10
5
2.5인데 parseInt 니까 2
1.25 // 1
0.625 // 0B
다음과 같은 코드의 시간 복잡도를 올바르게 나타낸 것은?
for (let i = 0; i < n; i++) {
i *= k;
}안에 있는 k는 무관하지 않을까 해서 O(n)을 선택했는데ㅋㅋㅋ i가 k랑 곱해지는 것을 놓쳤다!!;
연산횟수를 꼭 기억하자.
k룰 몇번 곱해야 n보다 커질까? k/n
logk(n)= ?
O(logk n), O(log n)도 맞음

