오답도 풀이하지만, 맞춘 것 중에서도 확실한 이해를 위해 풀이를 하는 노트!
그래프에 대한 설명으로 틀린 것을 모두 고르면?
A 정점(vertex)과 간선(edge)로 이루어져 있다.
B 간선이 방향을 가지는 방향 그래프와, 간선에 방향이 없는 무향 그래프로 나뉜다.
C 순환 구조를 가질 수 있다.
D 루트 정점이 존재한다.
E 그래프의 간선은 모두 같은 가중치 값을 가져야 한다.
정답은 맞췄는데 E가 이해가지 않았다. 가중치 값이란 무엇인가?
검색해보니 가중그래프란 것이 존재한다. 이 그래프는 정점 사이의 잇는 간선에 가중치(비용)이 주어진 그래프로, 쉽게 생각하면 정점은 '도시'고 간선이 '도로'라고 할 때, 가중치는 '통행료'라고 보면 된다.(최단거리 및 통행료 내비게이션을 생각하자)
가중치는 비교하기 위해 존재! 그리고 그 값은 같을 수도 있고 다를 수 있으므로 E는 틀린 답.
참고사이트 : https://ddmix.blogspot.com/2015/06/cppalgo-21-weighted-graph.html
D,E
정점의 개수가 5개인 방향 그래프의 최대 간선 개수는? (단, 자기 간선, self edge, self loop은 없다고 가정한다.)
- n(n-1)의 공식을 찾아서 대입해서 맞췄다.
무방향 그래프에서는 n(n-1)/2로 계산하고, 방향그래프에서는 n(n-1)로 계산한다.
20
다음 그래프에서 Vertex C의 in degree와 out degree의 합은?
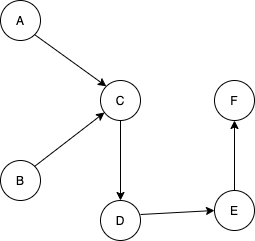
- 오답 : 5
문제를 잘못 읽고 풀었다.ㅠ..ㅠ.. C 정점의 진입,진출차수로 봤어야하는데 정점을 체크 안 하고 풀었다.
C는 진출차수가 1개 있고, 진입차수가 2개 있다. 고로 3!
3
그래프를 인접 행렬(Adjacent Matrix)로 구현할 때의 공간 복잡도는? (V = Vertex, E = Edge)
O(V^2) : 간선 개수와 무관
그래프를 인접 리스트(Adjacent List)로 구현할 때의 공간 복잡도는? (V = Vertex, E = Edge)
O(V+E)
위의 두 문제는 시간 복잡도만 봤고 공간복잡도는 못 봐서 검색해서 맞췄다. 참조사이트
오피스아워에서 쉬운 예제로 설명을 도와주셨다.
A,B,C라는 친구가 있을 때,
- A는 B,C를 팔로우했다
- B는 A를 맞팔하고, C를 팔로우했다.
- C는 아무도 팔로우하지 않았다
위의 경우를 인접행렬로 표현했을 때, 아래와 같다
// 팔로우하면 1, 팔로우 아니면 0
let followMat = [
[0,1,1] // A
[1,0,1] // B
[0,0,0] // C
]followMat의 공간복잡도는 O(3^2)으로 '9'가 된다.
인접 리스트의 경우로 생각할 경우, 아래와 같이 이해가 쉽게 리스트로 예시를 들어주셨다.
node{ A, follow: B } --- node{ B, follow: C } --- node{ C, follow : null }
node{ B, follow: A } --- node{ A, follow: C } --- node{ C, follow : null }
node{ C, follow: null }그림으로 표현하게 되면, 아래와 같으므로
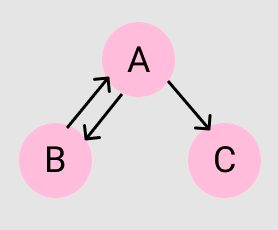
정점 : 3개(A,B,C)
간선 : 3개(A,B),(A,C),(B,A)
고로 인접리스트의 공간복잡도는 O(3+3) = '6' 이 된다.
메모리 사용량으로 보면 인접리스트가 덜 차지하는 것으로 보면 된다.
그래프의 시간 복잡도와 관련하여, 각 빈칸에 들어갈 말로 가장 적합한 것을 고르시오.
- 정점의 추가는 ( ) 방식이 효율적이다.
- 정점의 삭제는 ( ) 방식이 효율적이다.
- 간선의 추가와 삭제가 빈번히 일어나는 경우에는 ( ) 방식이 효율적이다.
- 오답 : 인접 행렬, 인접리스트, 인접행렬
인접행렬에서 정점은 추상화된다.
검색을 통해 간선이 많이 존재하는 밀집 그래프에 인접행렬이 유리하다고 해서 가장 마지막은 인접행렬이 효율적임을 인지했다. 사실 추가/삭제는 행렬보다 리스트가 효율적임을 연결리스트에서 경험했는데, 답 선택할 때 해석을 잘못한 것 같다.
(인접 리스트, 인접 리스트, 인접 행렬)
다음 이진 탐색 트리에 대한 설명 중 틀린 것을 모두 고르면?
A 자식 노드를 최대 2개까지 가질 수 있다.
B 항상 왼쪽 서브트리에는 작은 값이, 오른쪽 서브트리에는 큰 값이 존재한다.
C 이진 탐색 트리는 항상 완전 이진 트리다.
D 원하는 값을 찾기 위해서 최대 트리의 높이(h)만큼의 탐색이 필요하다.
E 자식 노드의 값 보다 부모 노드의 값이 항상 크다.
D가 헷갈렸다. 이진탐색트리가 한쪽으로 완전 치우쳐져 있을 경우, 높이가 정점의 갯수랑 동일해지므로 맞는 말.
C,E
이진 탐색 트리에서 child가 2개인 노드를 삭제하는 방법은 일반적으로 2가지가 있다. 이 방법을 적용하여 아래 이진 탐색 트리에서 21을 삭제했을 때, 새로운 루트 노드가 되는 값은 각각 무엇인가? (순서무관)
검색해서 맞췄다(참조사이트). 왼쪽 서브트리에서는 가장 큰값이 오고, 오른쪽 서브트리에서는 가장 작은 값이 온다.
더 쉽게 이해한다면, 루트노드에 가장 가까운 큰 값과 작은값이 위치한다고 이해하면 좋다.(중위값)
19,25
해설 : 21 삭제 후, 오른쪽 서브트리의 최소값을 새로운 루트 노드로 변경했을 때 이진 탐색 트리의 형태는 다음과 같습니다. 이미지 링크: https://go.aws/3b7pC6J
이진 탐색 트리에서 노드의 추가(insertion), 삭제(deletion), 조회(retrieval)의 시간 복잡도를 순서대로 나열한 것은?
O(log n),O(log n),O(log n)
→ 밸런스가 잘 맞춰진 BST에서 가능
극단적인 경우의 BST(Skewed)는 O(N) 시간복잡도를 가진다.
Degenerate 이진탐색서치
→ 이를 방지하기 위해, 추가할 때마다 3개씩 정도(45도) 비틀어서 밸런스를 맞츨 수 있다.
O(N), O(N), O(N)

