Support Vector Machine (SVM)
- 딥러닝 이전에 분류에서 뛰어난 성능으로 많이 사용되었던 분류 모델
- 중간 크기의 데이터셋과 특성이(Feature) 많은 복잡한 데이터셋에서 성능이 좋은 것으로 알려져있다.
선형(Linear) SVM
선 (1)과 (2)중 어떤 선이 최적의 분류 선일까?
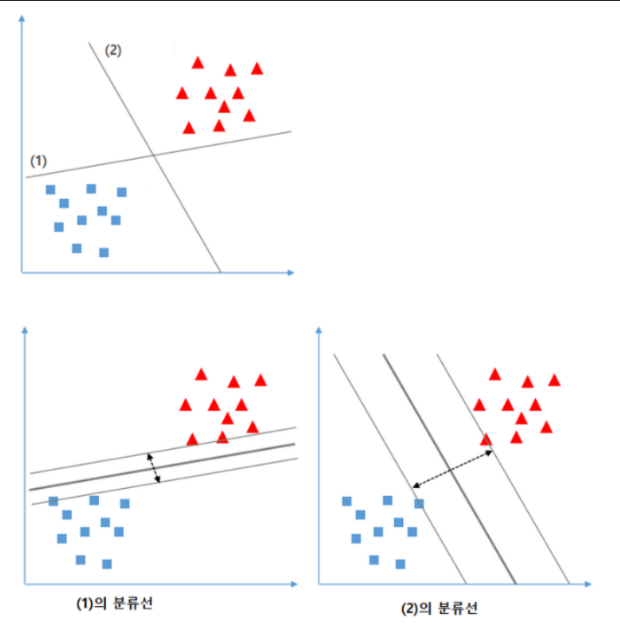
(2) 가 최적의 분류를 위한 경계선이다. 이유는 각 클래스의 별로 가장 가까이 있는 데이터간의 거리가 가장 넓기 때문이다. 넓다는 것은 그만큼 겹치는 부분이 적다는 것이므로 새로운 데이터를 예측할 때 모호성이 적어져서 맞을 확률이 더 높아지게 된다. SVM 모델은 두 클래스 간의 거리를 가장 넓게 분리할 수있는 경계선을 찾는 것을 목표로 한다.
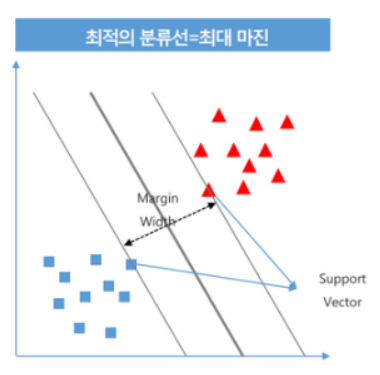
SVM 목표: support vector간의 가장 넓은 margin을 가지는결정경계를 찾는다.
- Support Vector
- 양 클래스간에 가장 가까이 있는 값들을 말한다.
- 결정경계 기준으로 양 클래스의 값들 중 결정경계와 가장 가까이 있는 값들이다.
- margin
- 두 support vector간의 너비
- SVM 모델은 최대 마진(margin)을 만드는 결정경계를 찾는다.
결정경계(Decision boundary)란
- 분류 문제에서 클래스들을 구분/분리하는 기준이다.
- 분류 모델들은 학습시 train dataset을 이용해 결정경계를 찾는다.
Hard Margin, Soft Margin
- SVM은 데이터 포인트들을 잘 분리하면서 Margin 의 크기를 최대화하는 것이 목적이다.
- Margin의 최대화에 가장 문제가 되는 것이 Outlier(이상치) 들이다.
- Train set의 Outlier들은 Overfitting에 주 원인이 된다.
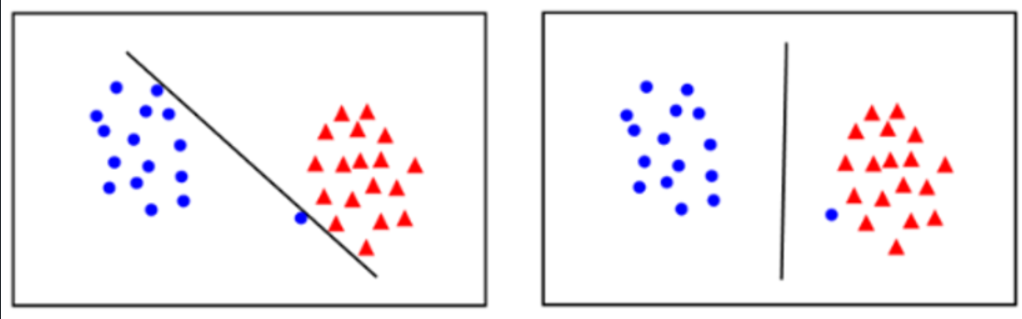
- Margine을 나눌 때 Outlier을 얼마나 무시할 것인지에 따라 Hard margin과 soft margin으로 나뉜다.
- Hard Margin
- Outlier들을 무시하지 않고 Support Vector를 찾는다. 즉 어떤 데이터 포인트도 결정경계를 침범하지 않도록 한다. 그래서 Support Vector간의 거리(margin)이 매우 좁아 질 수 있다.
- 선형적으로 분리가능할 때는 잘 작동하지만 그렇지 않을 경우 overfitting 문제가 발생할 수 있다.
- Soft Margin
- 일부 Outlier들을 무시하고 Support Vector를 찾는다. 즉 일부 데이터 포인트가 결정경계를 침범하여 잘못 분류되는 것을 허용한다. 그래서 Support Vector간의 거리(margin)을 넓힐 수있다.
- 무시 비율을 하이퍼파라미터
C로 정한다. 무시비율이 너무 커지면 underfitting 문제가 발생할 수 있다.
Hard/Soft margin 설정 하이퍼파라미터 C
- SVM의 규제 하이퍼파라미터.
- 잘못 분류 되는 것을 허용하는 비율 설정 하이퍼파라미터.
- 노이즈가 있는 데이터나 선형적으로 분리 되지 않는 경우 C값을 조정해 마진을 변경한다.
- 기본값 1
- 값이 클 수록 무시비율을 낮게 해서 규제를 약하게 한다. 너무 크게 설정 하면 overfitting이 일어날 수 있다.
- 작을 수록 무시비율을 높여 규제를 강하게 한다. 너무 작게 설정 할 경우 underfitting이 일어날 수 있다.
- Overfitting이 발생하면 값을 작게, Underfitting이 발생하면 크게 조정한다.
Kernel SVM (비선형(Non Linear) SVM)
비선형데이터 셋에 SVM 적용
- 선형으로 분리가 안되는 경우는?
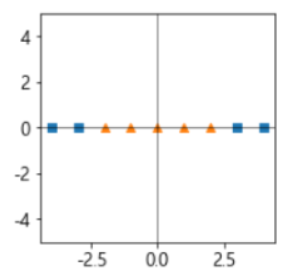
- 다항식 특성을 추가하여 차원을 늘려 선형 분리가 되도록 변환
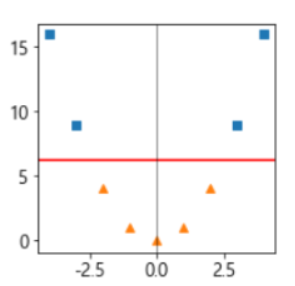
[2차원으로 변환 항 추가]
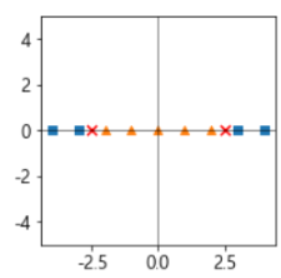
[원래 공간으로 변환]
Kernel trick(커널 트릭)
- 비선형 데이터셋을 선형으로 분리하기 위해 차원을 변경해야 하는데 이때 사용하는 함수를 Kernel이라고 하고 차원을 변경하는 것을 kernel trick 이라고 한다.
- 대표적인 kernel함수
- Radial kernel
- Polynomial kernel
- Sigmoid kernel
- 대표적인 kernel함수
Non linear SVM 모델의 하이퍼파라미터
- C
- Softmargin과 hard margin 적용 값
- gamma
- 비선형 결정정계를 얼마나 유연하게 만들 지 조절하는 규제 하이퍼파라미터.
- Linear SVM의 경우 gamma 값의 영향을 받지 않는다.
- 개별 데이터포인트가 결정 경계를 만드는데 어느 정도 영향력을 주는지를 설정하는 값이다.
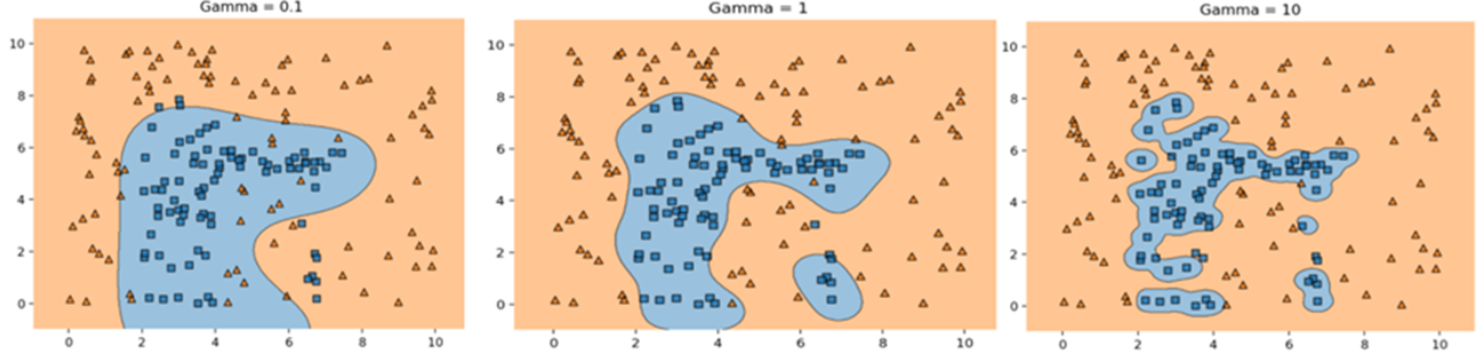
- 값을 크게 하면 개별 데이터 포인트의 결정 경계의 굴곡에 대해 영향을 미치는 범위가 작아져 결정 경계가 데이터 포인트 주변으로 좁혀져 개별 데이터 포인트에 민감하게 반응한다. (약한 규제) 너무 크게하면 overfitting이 발생할 수 있다.
- 값을 작게 하면 개별 데이터 포인트의 결정 경계의 굴곡에 대해 영향을 미치는 범위가 넓어져 부드러운 결정 경계를 만들고 개별 데이터 포인트에 민감하게 반응하지 않는다. (강한 규제) 너무 작게 하면 underfitting이 발생 할 수 있다.
- Overfitting이 발생하면 값을 작게, Underfitting이 발생하면 크게 조정한다.
- 비선형 결정정계를 얼마나 유연하게 만들 지 조절하는 규제 하이퍼파라미터.
gamma 값에 따른 결정경계 형태
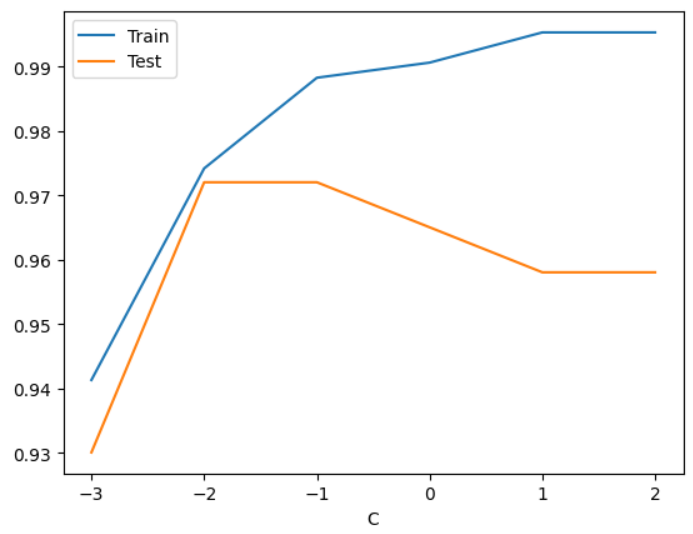
from sklearn.datasets import load_breast_cancer from sklearn.model_selection import train_test_split X, y = load_breast_cancer(return_X_y=True) X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=1)##### SVM 전처리 ### 연속형(수치형) - Feature scaling ### 범주형 - One Hot Encoding from sklearn.preprocessing import StandardScaler #, OneHotEncoder scaler = StandardScaler() X_train_scaled = scaler.fit_transform(X_train) X_test_scaled = scaler.transform(X_test) # Linear SVM - hyper parameter: C C_list = [0.001, 0.01, 0.1, 1, 10, 100] train_acc_list = [] test_acc_list = []from sklearn.svm import SVC # SVR: 회귀, SVC: 분류 from sklearn.metrics import accuracy_score for C in C_list: svm = SVC( kernel="linear", # 커널 함수 지정. 선형SVM: linear, 비선형SVM: rbf(기본), poly, sigmoid C=C, # soft - hard margin 설정. (작을수록 강한 규제) # gamma=100, # 비선형 svm의 hyperparameter random_state=0 ) svm.fit(X_train_scaled, y_train) pred_train = svm.predict(X_train_scaled) pred_test = svm.predict(X_test_scaled) train_acc_list.append(accuracy_score(y_train, pred_train)) test_acc_list.append(accuracy_score(y_test, pred_test))import pandas as pd import numpy as np df = pd.DataFrame({ "C":np.log10(C_list), "Train": train_acc_list, "Test": test_acc_list }) df.set_index("C")
df.set_index("C").plot();
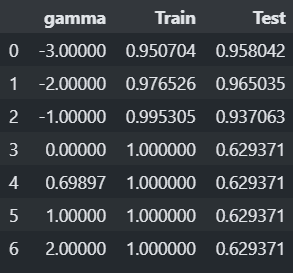
### 비선형 SVM. Hyper Parameter - C: soft/hard margin 규제, gamma (기본: 1) # gamma 변경에 따른 성능 변화. gamma_list = [0.001, 0.01, 0.1, 1, 5, 10, 100] train_acc_list = [] test_acc_list = [] for gamma in gamma_list: svm = SVC(kernel="rbf", C=1, gamma=gamma) # kernel기본값: rbf svm.fit(X_train_scaled, y_train) train_acc_list.append(accuracy_score(y_train, svm.predict(X_train_scaled))) test_acc_list.append(accuracy_score(y_test, svm.predict(X_test_scaled)))df = pd.DataFrame({ "gamma":np.log10(gamma_list), "Train":train_acc_list, "Test":test_acc_list }) df
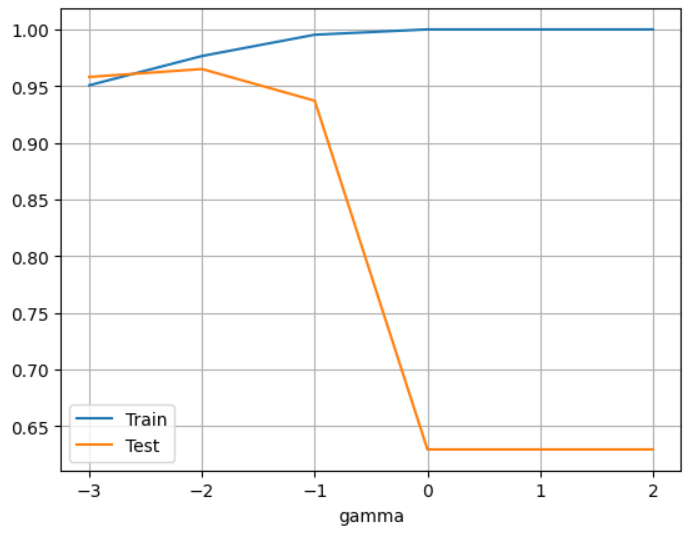
df.set_index("gamma").plot(grid=True);
ROC AUC score, AP score
from sklearn.metrics import roc_auc_score, average_precision_score # roc_auc_score(정답, 추정한 양성의 확률) -> model.predict_proba(X)[:, 1] svm = SVC(probability=True) # probability=True 설정해야 predict_proba() 사용가능. svm.fit(X_train_scaled, y_train) pos_proba = svm.predict_proba(X_train_scaled)[:, 1] print(roc_auc_score(y_train, pos_proba)) print(average_precision_score(y_train, pos_proba))0.997880008479966
0.9985299004450608
GridSearch로 최적의 조합찾기
GridSearchCV 생성 및 학습
- LinearSVC: C
- RBF SVC: C, gamma
from sklearn.datasets import load_breast_cancer from sklearn.model_selection import train_test_split X, y = load_breast_cancer(return_X_y=True) X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=1)### Pipeline -> 1) scaler 2) svm from sklearn.pipeline import Pipeline from sklearn.model_selection import GridSearchCV from sklearn.preprocessing import StandardScaler from sklearn.svm import SVC pipeline = Pipeline([ ("scaler", StandardScaler()), ("svm", SVC(random_state=0, probability=True)) ]) params = { "svm__kernel":["linear", "rbf", "poly", "sigmoid"], "svm__C": [0.001, 0.01, 0.1, 1, 10, 100], "svm__gamma": [0.001, 0.01, 0.1, 1, 10, 100] } gs = GridSearchCV(pipeline, params, scoring=["accuracy", "average_precision", "roc_auc"], refit="accuracy", cv=4, n_jobs=-1) gs.fit(X_train, y_train)
### 결과 확인 gs.best_params_{'svmC': 10, 'svmgamma': 0.01, 'svm__kernel': 'rbf'}
gs.best_score_0.9836007758772702
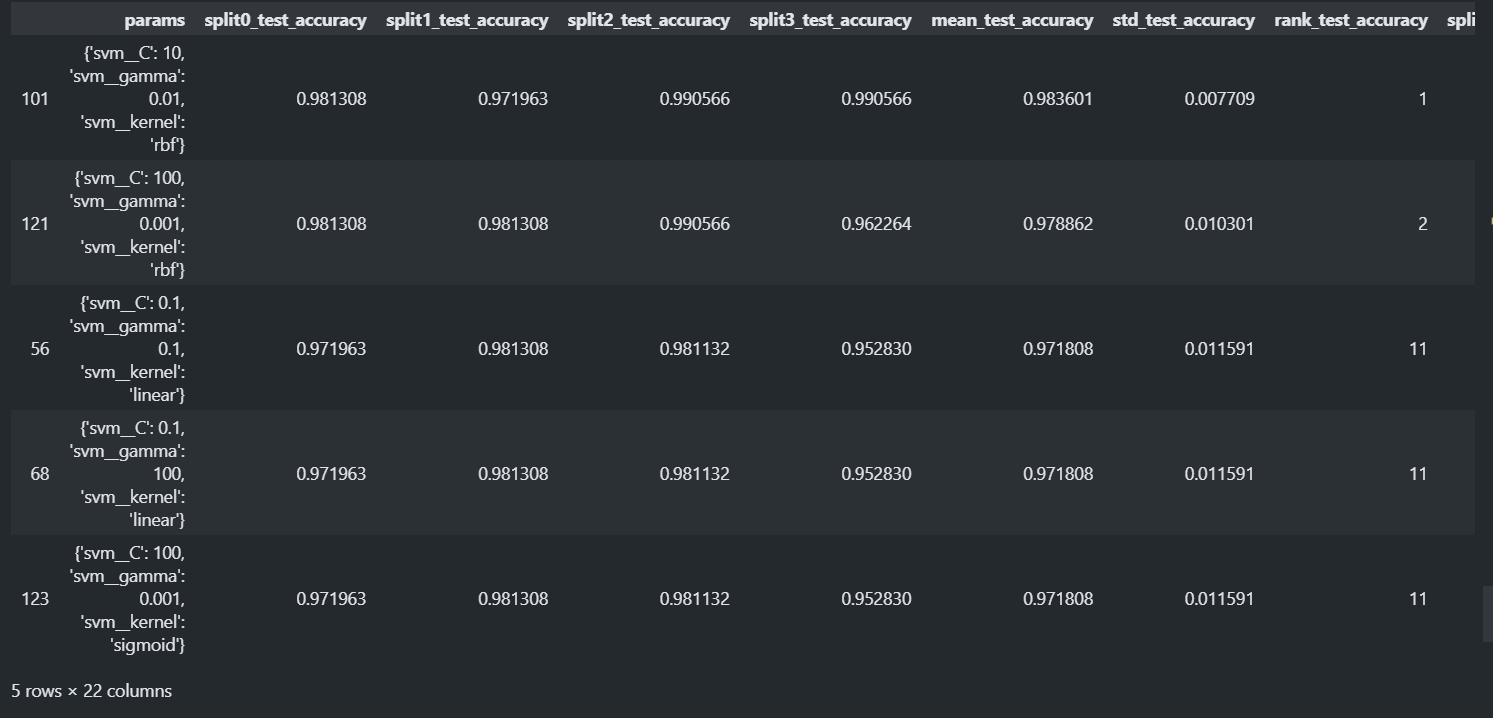
pd.options.display.max_colwidth = 100 # 컬럼의 값을 몇글자 까지 다 보여줄지. result = pd.DataFrame(gs.cv_results_) result.sort_values("rank_test_roc_auc")[result.columns[7:]].head()
# 최종평가 best_model = gs.best_estimator_ pred_test = best_model.predict(X_test) accuracy_score(y_test, pred_test)0.972027972027972