프로그래머스 억억단을 외우자
https://school.programmers.co.kr/learn/courses/30/lessons/138475

문제

---

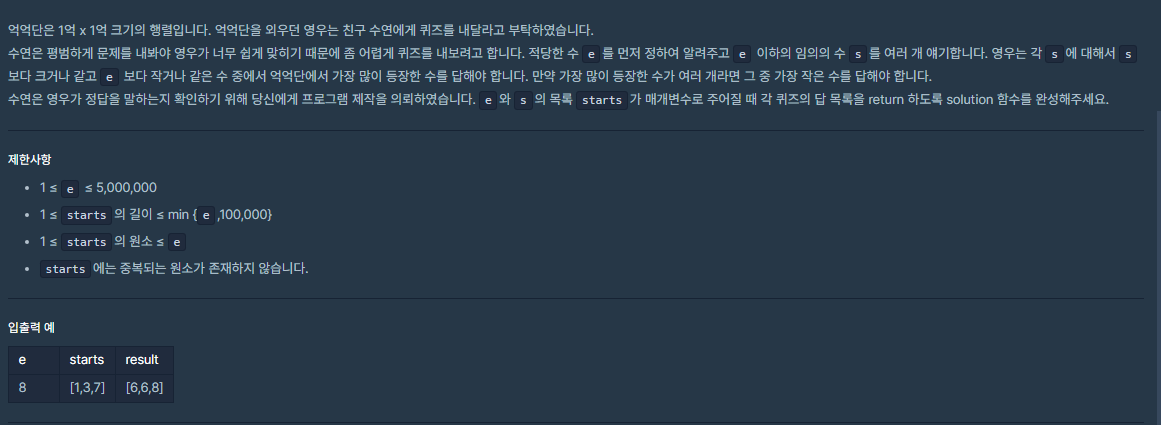
생각하기

---

• 최적화를 (아주 중요하게) 고려해야 하는 문제이다.

  • DP를 적용해야 하는 문제

• 조건부에 따라서 정렬을 해야하기 때문에 정렬 구현체를 만들어야 한다.

  • 기왕 정렬하는 거 PriorityQueue를 쓰기로 생각했음

동작

memo배열에 담아서 DP를 구현했으므로 그냥 정렬했으면 그만이긴 한데,

PriorityQueue가 정렬하는 데는 훨씬 수월할 것 같아서 pque를 사용했다.

pque와 tempPque로 PriorityQueue가 있는 이유는 poll()을 해야 PriorityQueue의 정렬에 맞는 순서가 제대로 나오기 때문인데,

poll()을 하고 난 다음 다른 곳에 값을 저장하고 있어야 반복해서 tempPque를 사용할 수 있기 때문에 2개의 PriorityQueue를 사용했다.

참고 사항으로
PriorityQueue의 성능은 O(logN)이고, 전체를 스캔할 때는 O(N)
Array.sort()의 성능은 O(NlogN)으로 가장 느리다고 합니다

가장 우수한 후보 하나만 뽑을 때는 당연히 PriorityQueue가 성능이 압도적으로 좋습니다.

logN >> N >> NlogN 의 셋 차이는 데이터가 1억개 일 때 logN은 몇십 번의 연산으로 끝나지만, N이나 NlogN은 몇 억 번의 연산을 필요로 합니다.

코드

---

Kotlin

import java.util.*

class Solution {
    // 우선순위 큐
    private var pque: PriorityQueue<Point> = PriorityQueue()
    private var tempPque: PriorityQueue<Point> = PriorityQueue()


    // 메모이제이션
    private lateinit var memo: Array<Point>

    private data class Point(
        var n: Int?,
        var c: Int?
    ) : Comparable<Point> {
        // Point 정렬 조건 -> c역순, n 정순으로 정렬
        override fun compareTo(other: Point): Int {
            if (c!! < other.c!!) {
                return 1
            } else if (c!! > other.c!!) {
                return -1
            } else {
                if (n!! > other.n!!) {
                    return 1
                } else if (n!! < other.n!!) {
                    return -1
                } else {
                    return 0
                }
            }
        }
    } // End of Point class

    fun solution(e: Int, starts: IntArray): IntArray {
        val size = starts.size
        val result = IntArray(size)

        DP(e)

        val pqueSize = pque.size
        for (i in 0 until size) {
            val s = starts[i]

            tempPque.forEach {
                pque.offer(it)
            }
            tempPque = PriorityQueue()

            for (j in 0 until pqueSize) {
                val temp = pque.poll()
                tempPque.offer(temp)

                if (temp.n!! >= s) {
                    result[i] = temp.n!!
                    break
                }
            }
        }

        return result
    } // End of solution

    fun DP(e: Int) {
        memo = Array(e) { Point(null, null) }
        for (i in 1..e) {
            memo[i - 1] = Point(i, 1)
        }

        // 각 수의 약수 갯수 모두 구하기
        for (i in 2..e step 1) {
            for (j in 1..(e / i) step 1) {
                memo[(i * j) - 1].c = memo[(i * j) - 1].c!! + 1
            }
        }

        memo.forEach {
            pque.offer(it)
        }
    } // End of DP
} // End of Solution class