RGB거리에는 집이 N개 있다. 거리는 선분으로 나타낼 수 있고, 1번 집부터 N번 집이 순서대로 있다.

집은 빨강, 초록, 파랑 중 하나의 색으로 칠해야 한다. 각각의 집을 빨강, 초록, 파랑으로 칠하는 비용이 주어졌을 때, 아래 규칙을 만족하면서 모든 집을 칠하는 비용의 최솟값을 구해보자.

1번 집의 색은 2번 집의 색과 같지 않아야 한다.
N번 집의 색은 N-1번 집의 색과 같지 않아야 한다.
i(2 ≤ i ≤ N-1)번 집의 색은 i-1번, i+1번 집의 색과 같지 않아야 한다.

🔎 문제 파악

📌 세번째 규칙에 의해 i와 i - 1(혹은 i + 1)사이의 관계가 수학적으로 정의된다.

📌 2차원 배열을 선언하고 첫번째 집에서 빨강, 초록, 파랑 중 하나를 선택한 세가지 경우에 대해 최솟값을 계산하고 다시 세가지 경우에서 가장 작은 수를 정답으로 선택한다.

🔑 DP(Dynamic Programming)

DP의 시작은 recurrence relation을 찾는 것이다.
i번 집의 색은 (i - 1)번째 선택한 색과 다른 두 색중 최소의 cost를 선택할 것이다.

i번째 집에 특정 색을 칠할 때 필요한 최소의 비용을 구하는 함수를 Cost(color, i)로, i번째에서 특정 색을 칠하는 데 필요한 cost를 COLOR(i)라 한다.

예를 들어, 4번째 집에 빨간색을 칠할 때의 드는 전체 최소의 비용은 Cost(red, 4)이고 4번째에 빨간색을 칠하는 데 드는 비용은 RED(4)이다.

또한, 4번째 집으로 빨간색을 골랐다면 3번째 집은 초록색이나 파란색 중 그 cost가 적은 것을 골라야 할 것이다.

이를 일반화하면 다음과 같다.

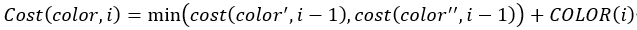
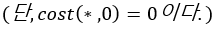
📚 자료구조

문제에서 주어진 입력의 형태는 다음과 같다.

첫째 줄에 집의 수 N(2 ≤ N ≤ 1,000)이 주어진다. 둘째 줄부터 N개의 줄에는 각 집을 빨강, 초록, 파랑으로 칠하는 비용이 1번 집부터 한 줄에 하나씩 주어진다. 집을 칠하는 비용은 1,000보다 작거나 같은 자연수이다.

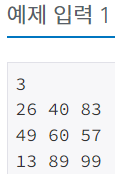
N번째 집을 색칠하는 과정을 색깔별로 정리하기 위해 2차원 배열 cost를 선언했다.
또한 현재의 N번째 집을 색칠하는 cost를 저장하기 위한 1차원 배열 color를 선언했다.
color에서는 반복문을 통해 각 단계의 빨강, 초록, 파란색의 cost만을 저장하고 다른 단계의 색깔별 cost는 저장하지 않을 것이다.

	int cost[1001][3]; 	//cost[*][0] -> R, cost[*][1] -> G, cost[*][2] -> B
	int color[3]; 		//color[0] -> R, color[1] -> G, color[2] -> B

🚀 최종 코드

#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <queue>
#include <vector>
#include <cmath>

using namespace std;

void baekjoon_1149() {
	int N;
	int cost[1001][3] = { 0,0,0, }; //Cost(*,0) = 0
	int color[3];
	scanf("%d", &N);
	for (int i = 1;i <= N;i++) {
		scanf("%d %d %d", &color[0], &color[1], &color[2]);
		cost[i][0] = min(cost[i - 1][1], cost[i - 1][2]) + color[0];
		cost[i][1] = min(cost[i - 1][0], cost[i - 1][2]) + color[1];
		cost[i][2] = min(cost[i - 1][0], cost[i - 1][1]) + color[2];
	}

	printf("%d", min(cost[N][0], min(cost[N][1], cost[N][2])));
	return 0;
}

https://github.com/Yg-Hong/algorithm/blob/main/Dynaminc_programming/Baekjoon_1149.cpp