이 문제는 아주 평범한 배낭에 관한 문제이다.

한 달 후면 국가의 부름을 받게 되는 준서는 여행을 가려고 한다. 세상과의 단절을 슬퍼하며 최대한 즐기기 위한 여행이기 때문에, 가지고 다닐 배낭 또한 최대한 가치 있게 싸려고 한다.

준서가 여행에 필요하다고 생각하는 N개의 물건이 있다. 각 물건은 무게 W와 가치 V를 가지는데, 해당 물건을 배낭에 넣어서 가면 준서가 V만큼 즐길 수 있다. 아직 행군을 해본 적이 없는 준서는 최대 K만큼의 무게만을 넣을 수 있는 배낭만 들고 다닐 수 있다. 준서가 최대한 즐거운 여행을 하기 위해 배낭에 넣을 수 있는 물건들의 가치의 최댓값을 알려주자.

입력

• 첫 줄에 물품의 수 N(1 ≤ N ≤ 100)과 준서가 버틸 수 있는 무게 K(1 ≤ K ≤ 100,000)가 주어진다. 두 번째 줄부터 N개의 줄에 거쳐 각 물건의 무게 W(1 ≤ W ≤ 100,000)와 해당 물건의 가치 V(0 ≤ V ≤ 1,000)가 주어진다.
• 입력으로 주어지는 모든 수는 정수이다.
• 예제입력

출력

• 한 줄에 배낭에 넣을 수 있는 물건들의 가치합의 최댓값을 출력한다.

🔎 문제 파악

📌 0/1 Knapsack 문제이다.

📌 각 물건을 선택한다면 현재 준서가 버틸 수 있는 무게에 선택한 물건의 무게를 빼서 다음번 선택으로 넘기고 선택하지 않는다면 버틸 수 있는 무게를 그대로 다음번 선택으로 넘긴다.

📌 재귀적으로 문제를 풀면 시간초과에 걸릴 확률이 크다. 2차원 배열을 선언하자.

🔑 DP(Dynamic Programming)

0/1 Knapsack 문제이므로 문제의 본질이 DP에 있다는 것을 확인했으니 recurrence relation을 찾아보자.

i번째 물건을 선택할 때, i번째 물건의 가치를 Pi , i번째 물건의 무게를 Wi라고 할 것이다.

i번째 물건 차례에서 버틸 수 있는 무게가 weight라 하면 그 때 얻을 수 있는 최대의 가치합을 Profit(i, weight)라 한다.

이를 일반화하면 다음과 같다.

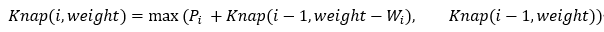
⭐️ 단, wegith - Wi가 음수라면 Profit()은 0이다.

📚 자료구조

각각의 물건의 가치와 무게를 저장하기 위한 int형 배열이 각각 하나씩 필요하다.
또한 DP계산을 위해서 입력의 최대치만큼 크기의 2차원 배열을 선언한다.

int W[101];
int P[101];
int knap[101][100001];

🚀 최종 코드

#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <queue>
#include <stack>
#include <vector>
#include <cmath>

using namespace std;

int W[101];
int P[101];
int knap[101][100001];

int main() {
	int N, K;
	scanf("%d %d", &N, &K);
	for (int i = 1;i <= N;i++) 
		scanf("%d %d", &W[i], &P[i]);
	
	int chosen, unchosen;

	for (int i = 1;i <= N;i++) {
		for (int weight = 1;weight <= K;weight++) {
			if (weight - W[i] >= 0) {
				chosen = knap[i - 1][weight - W[i]] + P[i];
				unchosen = knap[i - 1][weight];
				
				knap[i][weight] = max(unchosen, chosen);
			}
			else
				knap[i][weight] = knap[i - 1][weight];
		}
	}
	printf("%d", knap[N][K]);
}

⌛️ 문제 해설

int chosen 변수는 i번째 물건을 골랐을 때의 이익이고 int unchosen 변수는 i번째 물건을 고르지 않았을 때의 이익이다.
코드의 반복문이 진행되면 0~K까지의 무게가 주어졌을 때의 최대 이익이 계산된다.

예제를 입력하고 knap 2차원 배열의 모든 값을 출력해보았다.

---

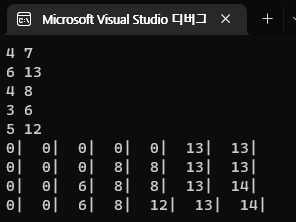
1번 물건에 대해서 (첫번째 행) ,
weight가 6일 때, 1번 물건을 선택할 수 있고 따라서 첫번째 행의 6번째 열은 이익의 최대합이 13이다. (knap[1][6] = 13)
weight가 7일 때, 이익의 최대합은 13 (knap[1][6]) + 0 (knap[1][1]) 이다.

---

2번 물건에 대해서 (두번째 행) ,
weight가 5일 때 (다섯번째 열) , 이익의 최대합은 0 (knap[1][1]) + 8 (P[2]) 이다.

chosen = knap[1][5 - W[2]] + P[2];	// 8
unchosen = knap[1][5];				// 0

weight가 6일 때, 이익의 최대합은 13 (knap[1][6])이다.

chosen = knap[1][6 - W[2]] + P[2];	// 8
unchosen = knap[1][6];				// 13

---

3번 물건에 대해서 (세번째 행) ,
weight가 7일 때, 이익의 최대합은 8 (knap[2][4]) + 6 P[3] 이다.

chosen = knap[2][7 - W[3]] + P[3];	// 14
unchosen = knap[2][6];				// 13

1번부터 N번까지 모든 물건을 넣어봤을 때 이익의 최대값은 knap[N][K]이므로 이를 출력해준다.

printf("%d", knap[N][K]);