AI/ML/Logistic Regression
로지스틱 회귀는 이진 분류를 해결하는데 사용되는 모델이다. (k-class 모델, k-class & ordinal 모델 등의 변형모델을 통해 다항 로지스틱 회귀도 가능하다.)
이진 분류는 분류문제 아닌가? 왜 회귀라는 말을 썼을까?
계산과정에서 Numerical data를 어쩌구.. 아무튼 회귀라고 부른다.
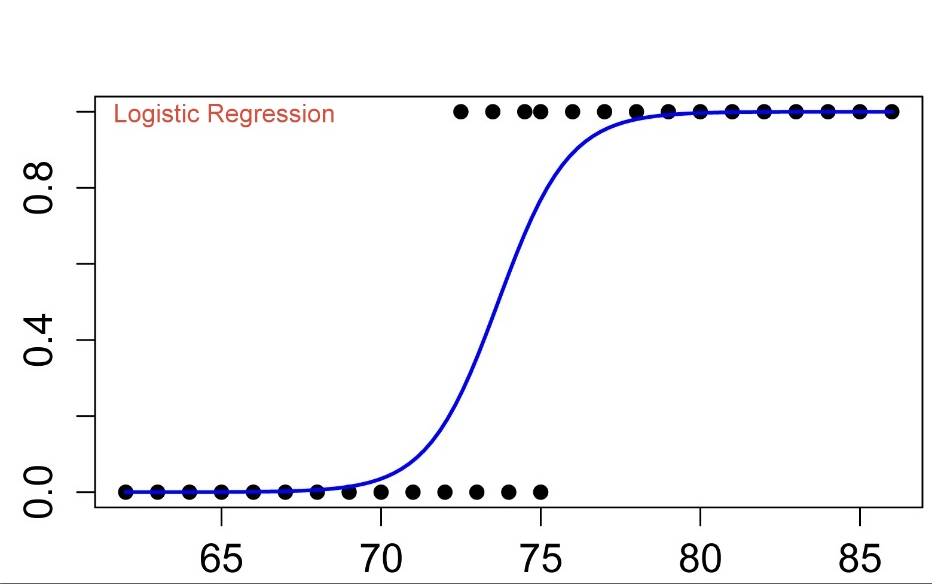
이진 분류라 데이터들이 0 혹은 1을 갖는다. 여기 파란 선은 sigmoid function으로, 선형회귀의 일차함수와 비슷한 역할을 한다. sigmoid function은 데이터의 실제 값이 1일 확률을 예측하여 보여준다.
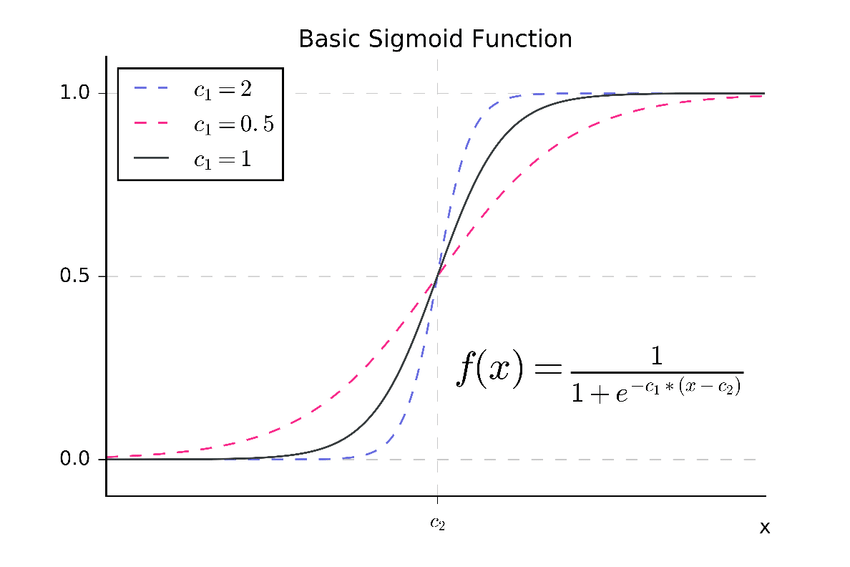
여기서도 세타의 조정을 통해 데이터에 함수를 근사한다. 선형회귀하고 매우 비슷한데 이래서 로지스틱 회귀라고 하는가보다.
로지스틱 회귀에서는 두 가지 정답을 제공할 수 있겠다. 확률과 확률에 기반한 판단이다.
양성 카테고리에 속할 가능성 0.134, 0.655 (scikit~~~.predict_proba(x_Data))
또는
0.6(cutoff)을 넘으니 양성, 못넘으니 음성 이렇게. (scikit~~~.predict(x_Data))
어떤 함수로 근사하는지 알았으면 모델을 학습시켜야한다.
학습의 기준은 Cost function이 된다. 이 목적함수를 최대한 줄이는 파라미터를 찾는다.
선형회귀에서는 일차함수가 들어갔기에 그의 제곱 모양인 MSE(평균제곱편차)도 이차함수 형태를 띄었다.
분류문제의 경우 정답 오답을 구분해서 정확도를 구할 수도 있으나 이게 그렇게 좋은방법인 것 같지는 않다. 정확도가 같다면 또 다른 수단을 사용해야 된다.
하지만 sigmoid 함수를 넣은 MSE는 모양이 기괴하다. 근데 자세한 이유는 아직 모름
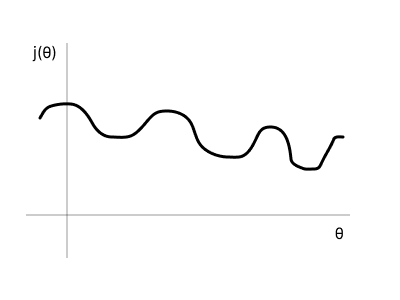
보통의 MSE들은 극소이면 최소일 것이라 예상하는 면이 있고 얼추 맞아떨어지는 경우가 많은데 이 경우는 전혀 그렇지 않다. 그래서 MSE가 아닌 Cross-Entropy라고 하는 cost function을 사용한다. 이는 분류문제에서 자주 사용된다.
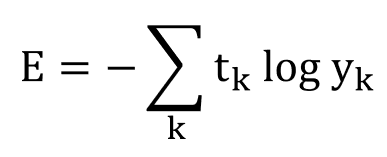
결과값에 로그를 씌우고 실제 정답을 곱해 합산한 것이다. 두 확률 분포의 차를 뜻한다.
https://hoya012.github.io/blog/cross_entropy_vs_kl_divergence/
이곳을 참고하면 더 자세히 배울 수 있다.

엔트로피는 information의 평균이다. information은 로그(확률)이다.
분류 문제들을 해결할 때 모델들은 단순하게 이게 class0이고 class1이고 딱 정해주지 않는다. 확률을 제공한다.
class0, class1, class2가 있을때는 [0.31, 0.68, 0.01] 이렇게 뱉는다.
이는 categorical value들을 한 행으로 쭉 늘어놓는 one-hot encoding이다. 과정은 encoding, 결과는 one-hot label로 부른다.
softmax
일련의 값들의 분포를 합이 1이 되도록 표준화하는 것
실습
from sklearn import linear_model
로지스틱 회귀도 선형모델 안에 있다.
아래는 데이터 정제 과정에서 사용됨
df[0].apply(function)
열.apply를 통해 데이터에 function을 일괄적용한 새로운 열을 리턴함
nparray[:, a:b], nparray[:, (2, 5, 9)]
numpy array 슬라이싱.
전자는 모든 행, a에서 b-1열까지 선택 / 후자는 모든 행, 2,5,9번 열만 선택
둘다 이차원 array를 가정한다.
다시 실습으로
x_train, x_test, y_train, y_test = model_selection.train_test_split(data_X, data_Y, test_size = 0.3, random_state = 0)데이터를 학습용, 테스트용으로 쪼갠다. 테스트용 데이터는 30%로. random_state(random seed)를 지정함으로써 다음번 실행에도 똑같이 데이터가 섞이고 분배된다.
model = linear_model.LogisticRegression()
model.fit(x_train, y_train)목적함수인 CEE(Cross-Entropy Error)를 최소화하도록 학습한다. 학습이 완료되면 테스트한다.
import sklearn.metrics import accuracy_score
pred_test = model.predict(x_test)
print(accuracy_score(pred_test, y_test))accuracy_score은 categorical data를 사용하는 분류문제에서만 사용된다.
accuracy말고 다른 방식으로 결과를 분석해보자.

한창 코로나 검사키트 나왔을때 위양성 위음성 어쩌구랑 같다.
앞은 예측치의 정답여부에 따라 True/False를 붙여주고 뒤는 예측으로 붙여주면 안 헷갈린다.
Accuracy는 (TP+TN)/(TP+TN+FP+FN)으로 구할 수 있다.
Recall(재현율) = TP/(TP+FN) 실제 참인 것중 예측 성공한 것
Precision(정밀도) = TP/(TP+FP) 참이라고 예측한 것들 중 실제로 맞은 것
많이 헷갈린다.
Recall은 참인 것에 대한 민감도를 의미한다. FP가 많더라도 FN을 줄여야 Recall을 끌어올릴 수 있다. 코로나같이 실제 양성을 구멍없이 잡아내야한다면 Recall이 중요하다.
Precision은 예측 실패에 대한 민감도이다. 진양성을 좀 못잡더라도 위양성을 줄여야한다. 되도록 예측에 실패하면 안되는 스팸메일 거르기같은 경우 Precision이 중요하다.
F1-Score는 Recall과 Precision의 조화평균이다. 둘다 고려할 경우 사용하면 된다.
여기서 확장하면 F-Beta Score를 사용할 수 있는데 Recall과 Precision에 가중치를 부여하여 점수를 계산할 수 있다.
ROC Curve & AUC
진양성율: 실제 양성인것들 중 진양성인 것들의 비율 TP/(TP+FN)
위양성율: 실제 음성인것들 중 위양성인 것들의 비율 FP/(TN+FP)
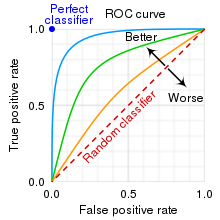
왼쪽 위로갈 수록 성능이 좋은것. 점선은 랜덤으로 찍었을 경우를 생각할 수 있다.
수직 위로가면 양성을 빠짐없이 잡아내고
수평 왼쪽으로 음성보고 양성이라고 하는 실수가 줄어든다(위양성)
사진에서 확인할 수 있듯이 한쪽을 개선하면 한쪽이 나빠지는 경향이 있다. 저 선은 cutoff를 조절해가면서 그려진다고 보면 된다.
선이 구불구불해서 성능비교가 힘들다면 적분해서 면적을 비교하면 된다. 이 면적이 AUC(Area Under the ROC Curve)이다.
실용
from sklearn.metrics import roc_curve, auc
pred_test = model.predict_proba(x_test)
fpr, tpr, _ = roc_curve(y_true=y_test, y_score=pred_test[:,1])
roc_auc = auc(fpr, tpr)y_score=pred_test[:,1] 이렇게 슬라이싱하는 이유는 model.predict_proba가 확률p와 1-p를 같이 제공하기 때문이다.
fpr과 tpr은 ROC Curve상 특정 점(꺾이는점)들의 x,y좌표를 뜻한다.
_는 굳이 필요없는 부분이다.
