Auto Correlation Funtion 과 Partial Auto Correlation Function을 통해서 어떻게 시계열 데이터에 인사이트를 뽑을 수 있을지 간단하게 알아보겠습니다.
이전 포스팅에서 사용했던 환율데이터를 사용하겠습니다.
import matplotlib.pyplot as plt
df['KOUS'].plot(figsize = (12,6) )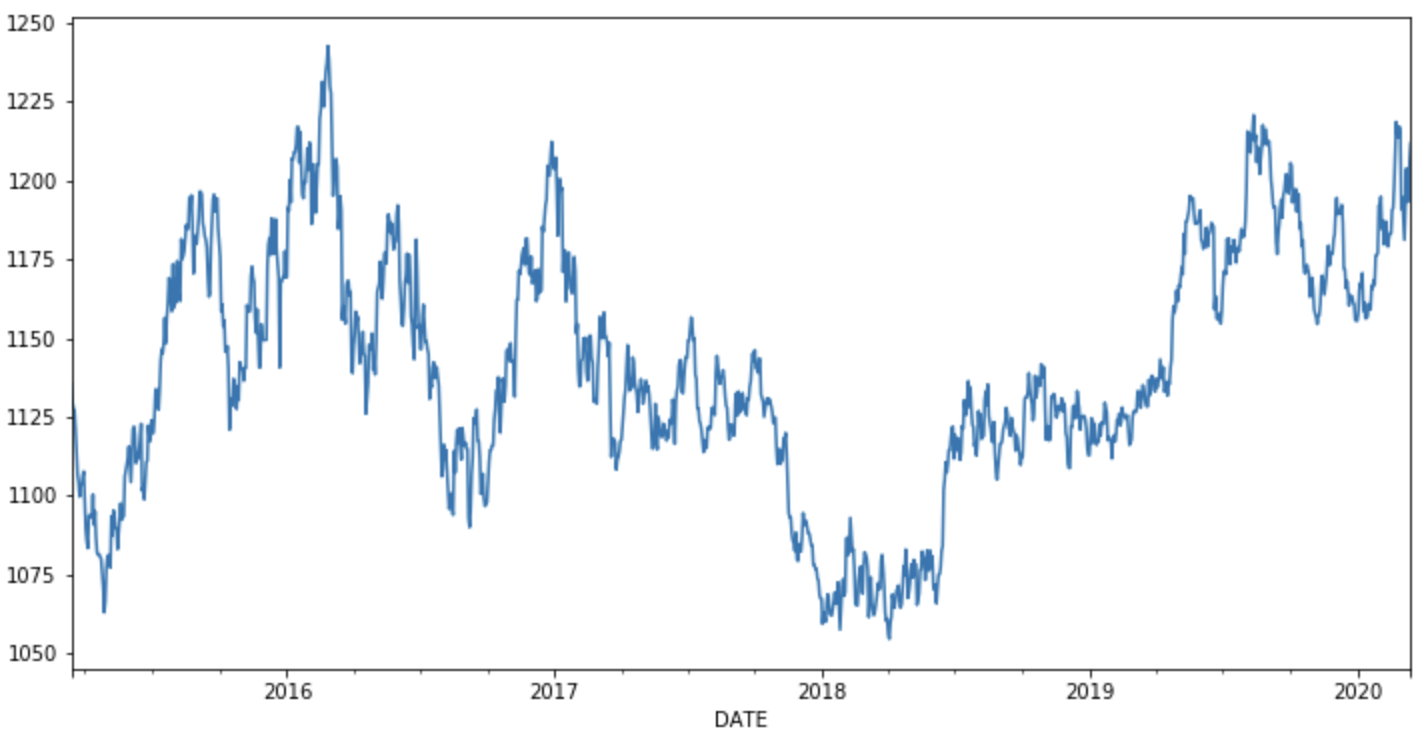
먼저 해당데이터는 일자별로 있기때문에 주단위 데이터로 변경해서 사용하겠습니다.
df_w =. f.resample('W-Fri').last()
df_w
변경된 데이터를 시각화 해보았습니다.
df_w.plot(figsize = (12, 6
))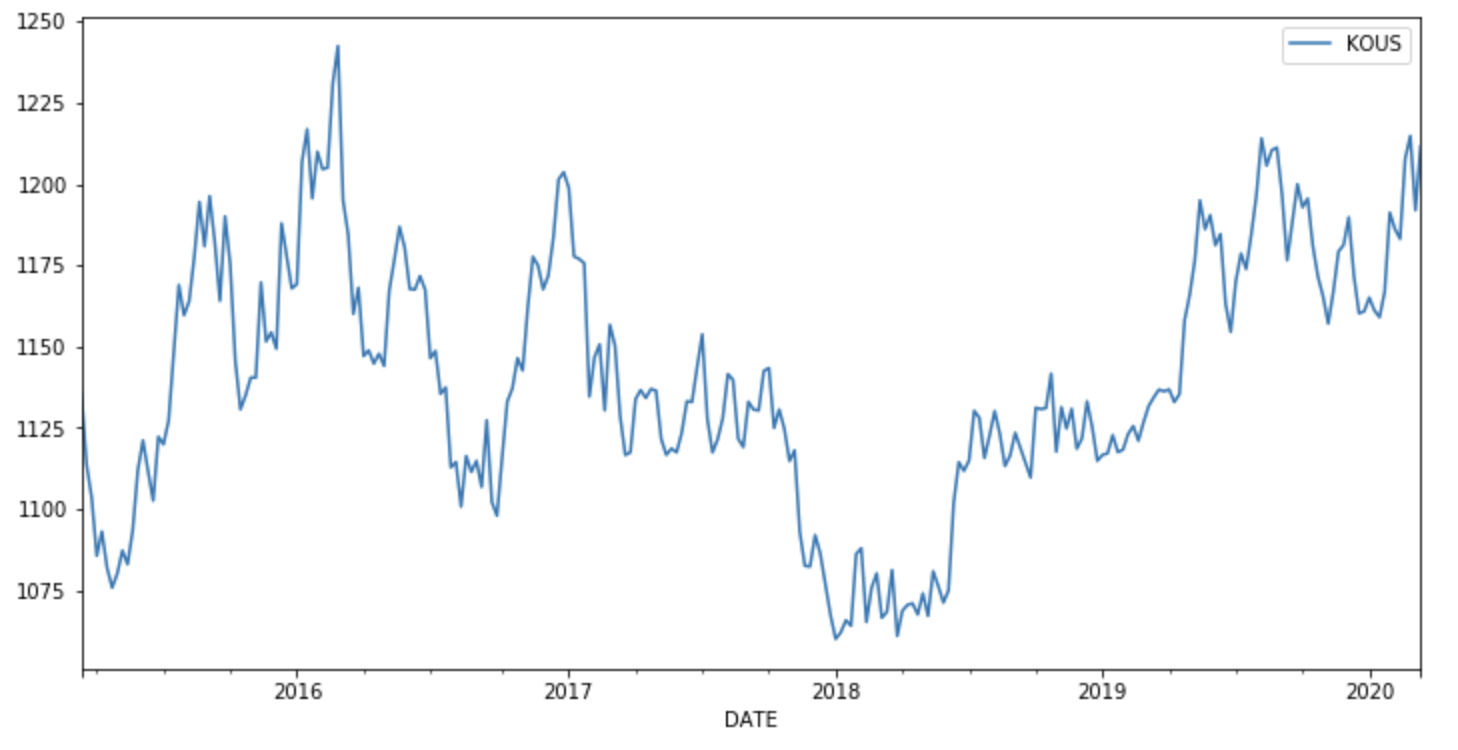
그래프를 잘 보시면 2017년에는 갑자기 상승을 했지만 금방 떨어진 반면, 2019년은 오래동안 상승후 유지를 하는 모습입니다. 이를 ACF와 PACF도표로 살펴보겠습니다.
# 2017년 2019년도 분리
df_2017 = df_w[df_w.index.year==2017]
df_2019 = df_w[df_w.index.year==2019]
# 분리된 데이터 시각화
fig, ax = plt.subplots(1,2, figsize = (12, 5))
df_2017.plot(ax = ax[0])
df_2019.plot(ax = ax[1])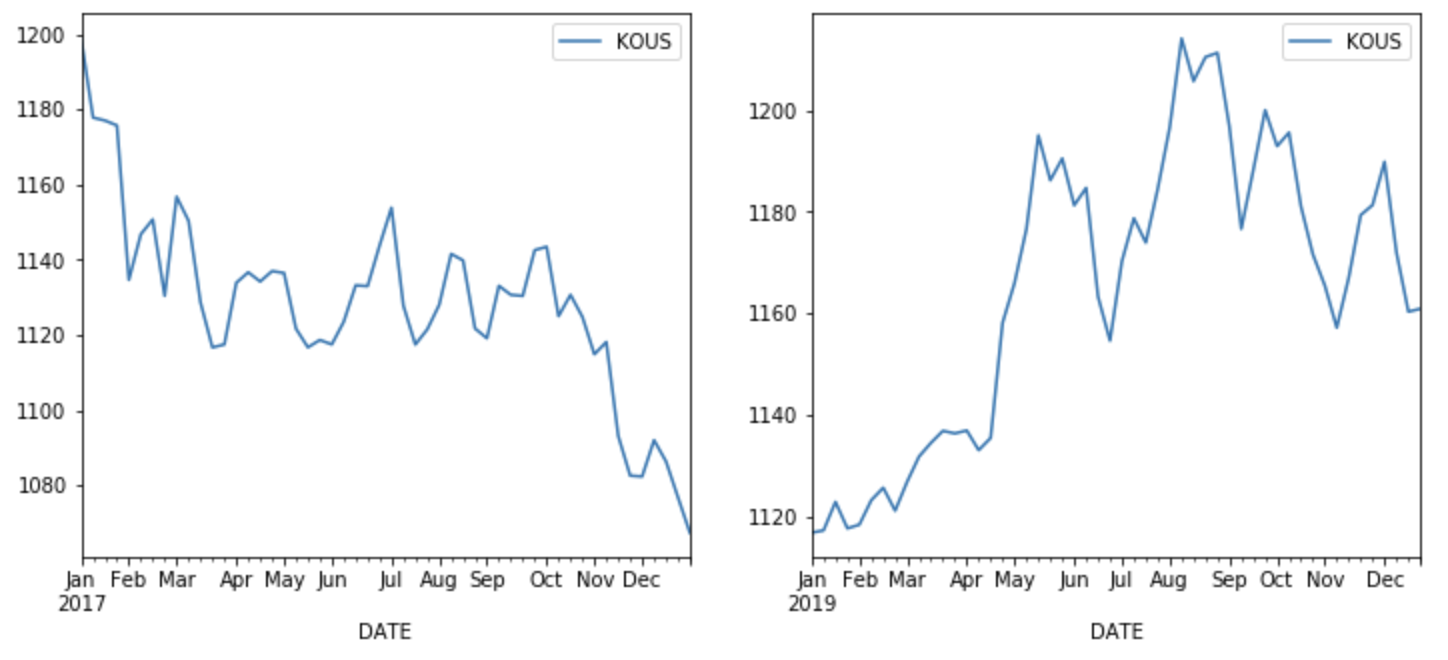
2017년이 왼쪽 2019년이 오른쪽입니다. 도표를 보시면 2017년은 금방 내려오는 모습이고 2019년은 상승해 있는모습입니다.
이것으로 어떤 인사이트를 발굴해 낼 수 있을까요
# ACF 도표그리기
fig, ax = plt.subplots(1,2 ,figsize = (12, 5))
plot_acf(df_2017, ax = ax[0])
plot_acf(df_2019, ax = ax[1])
plt.show()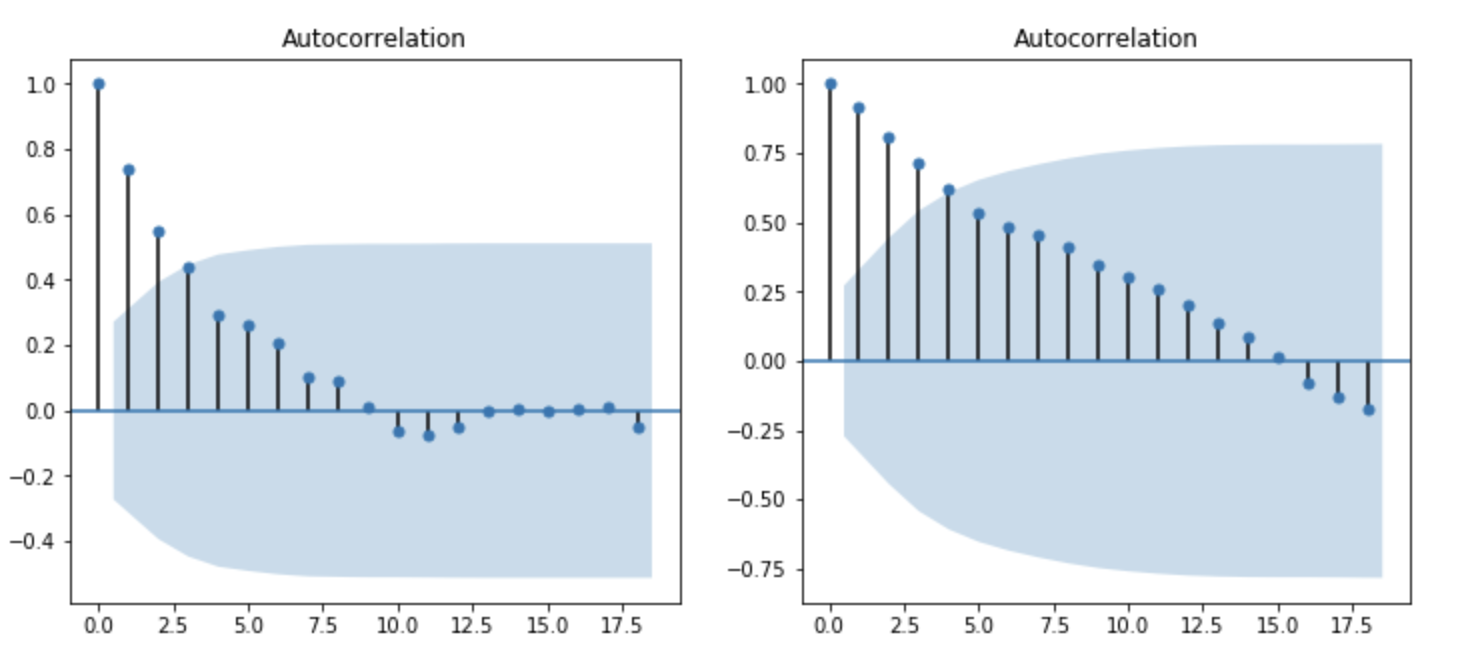
이전 글에서 알려주었던 ACF도표입니다. 왼쪽부터 보시면 시차가 3인 시점까지 상관관계가 있다는 것을 볼 수 있고, 오른쪽 도표를 보면 시차가 4~5까지 상관관계를 보이는것을 확인할 수 있습니다.
이게 무슨뜻일까요???
지금 보고 있는데이터는 위에서 말했든 환율에 대한 데이터입니다. 그리고 2017(왼쪽도표)년과 2019(오른쪽도표)년은 각각 시차가 3, 시차가 4일때 까지 상관관계를 보입니다. 즉, 2017년에는 외부의 어떤 요인에 의한 영향이 시차가 3인정도까지 미치는것이고 2019년은 외부요인에 의해 시차가 4까지 영향을 미친다는 것입니다.
이말은 외부의 어떤 요소가 영향을 미치는 기간을 뜻합니다. 요약하면 2017년은 시차가 3인만큼 지속되고 2019년은 시차가 4인 만큼 지속된다는 뜻입니다.
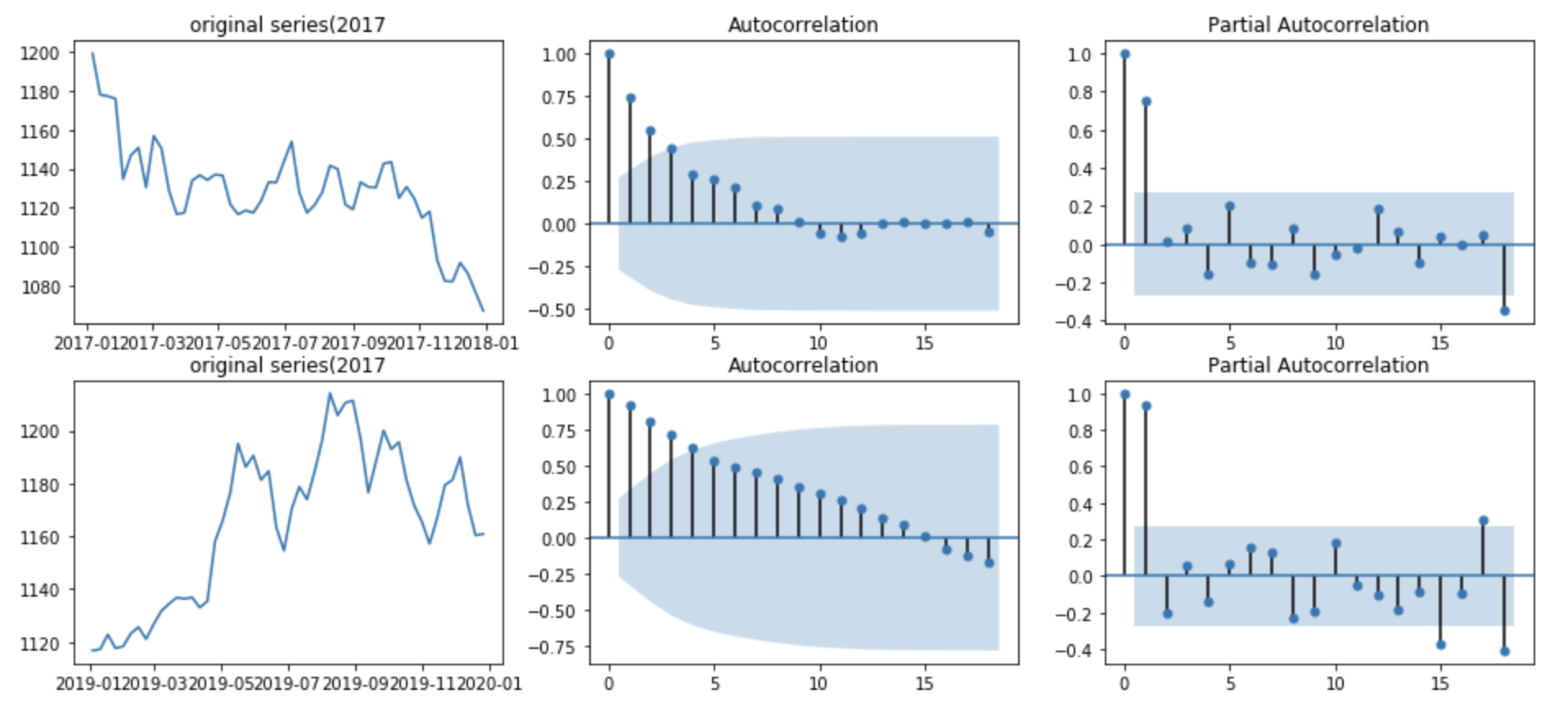
정리를 위해 지금까지 사용한 도표를 한번에 모아보았습니다.
fig, ax = plt.subplots(2,3,figsize = (16, 7))
ax[0,0].plot(df_2017)
ax[0,0].set_title('original series(2017')
ax[1,0].plot(df_2019)
ax[1,0].set_title('original series(2017')
plot_acf(df_2017, ax = ax[0,1])
plot_acf(df_2019, ax = ax[1,1])
plot_pacf(df_2017, ax = ax[0,2])
plot_pacf(df_2019, ax = ax[1,2])
plt.show()
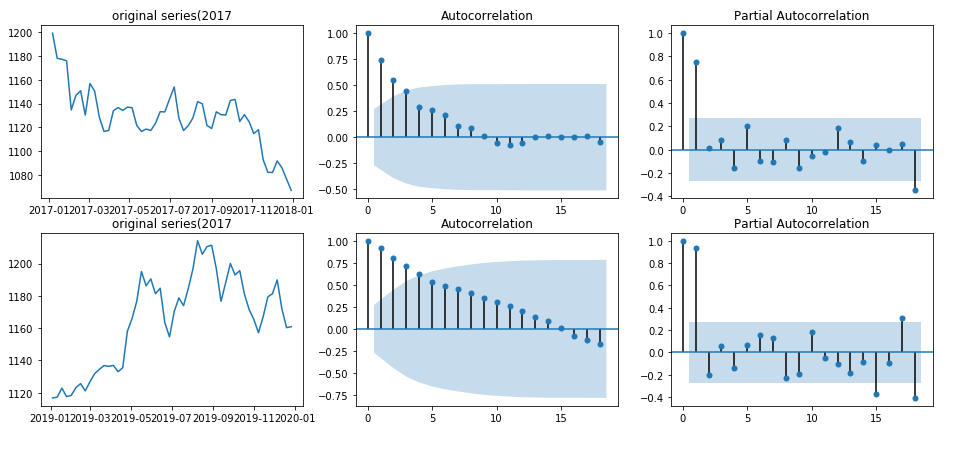
2017년과 2019년이 우리의 비교대상이었고,
두번째 행에서 ACF 도표를 통해 2017년보다 2019년이 외부요인에 좀 더 오래 지속됨을 알게되었다.
그리고 세번째 행의 PACF를 통해서 2019년의 경우 뒤로가면 상관관계가 높아지는 구간들을 볼 수 있어서 이부분을 추가적으로 살펴볼 필요가 있어보인다. 또한 PACF 도표를 보면 튀는것이 1개 인것을 알 수 있고 AR(1)모델을 사용해보면 되겠다는 것을 짐작해 볼 수 있습니다.
이렇게 간단하게 ACF 와 PACF도표를 통해서 상관관계를 외부요인으로 두어 얼마나 외부요인에 영향을 미치는지 해석을 해 볼수도 있다.
다른 예시들을 생각해보면, 주식차트 역시 외부요인에 얼마나 반응하는지 살펴볼 수 있고, B2C를 하는 회사에서 마케팅 효과를 분석해서 얼마나 마케팅효과가 가는지 확인해 보는 방법도 있다.
