시계열데이터

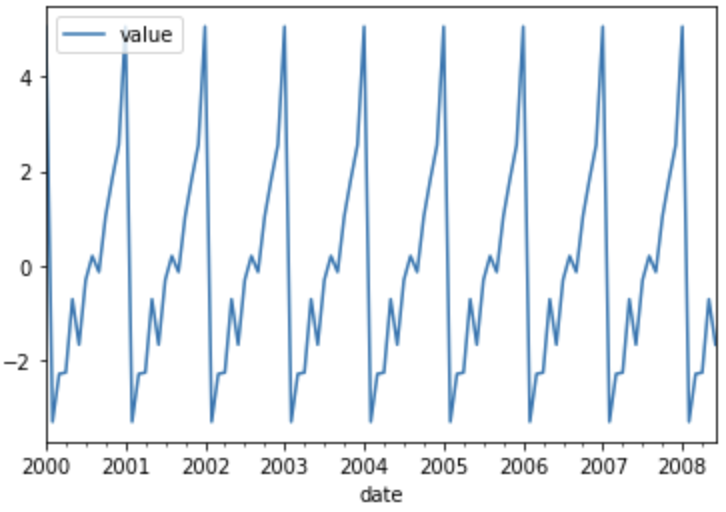
시계열 데이터 분해(Decomposition) 위와 같은 시계열 데이터(호주 당뇨병 치료약 월별 sales데이터)가 있다고 가정해보자. 시계열 데이터를 공부할때면 항상 초반에 데이터를 분해하는 내용을 다루고 있는데 왜 그러는것일까?? 다시한번 위에 있는 그래프를 보

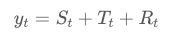
지난 포스팅에서는 시계열 데이터의 구성에 대해서 확인 해 보았고, 이번에는 시계열 데이터를 분해하는것을 직접 다루어 보려고 한다.먼저 분해 방법에는 두가지가 있다.각각의 변수를 먼저 설명하면, y는 데이터, S는 계절성분, T는 추세, R은 불규칙 요소를 나타나면 각각

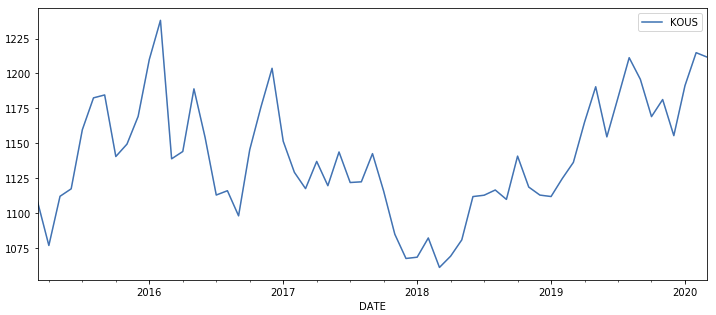
INDEX 정상성이란? 정상성 만족 여부 판별하기 정상성 변환(로그변환, 차분) 5. 정상성(stationary)이란? 시계열 데이터를 예측을 하는데 있어서 데이터의 분산이 모두 제각각이고, 계절성과 추세가 있다고 가정했을때 우리는 이러한 데이

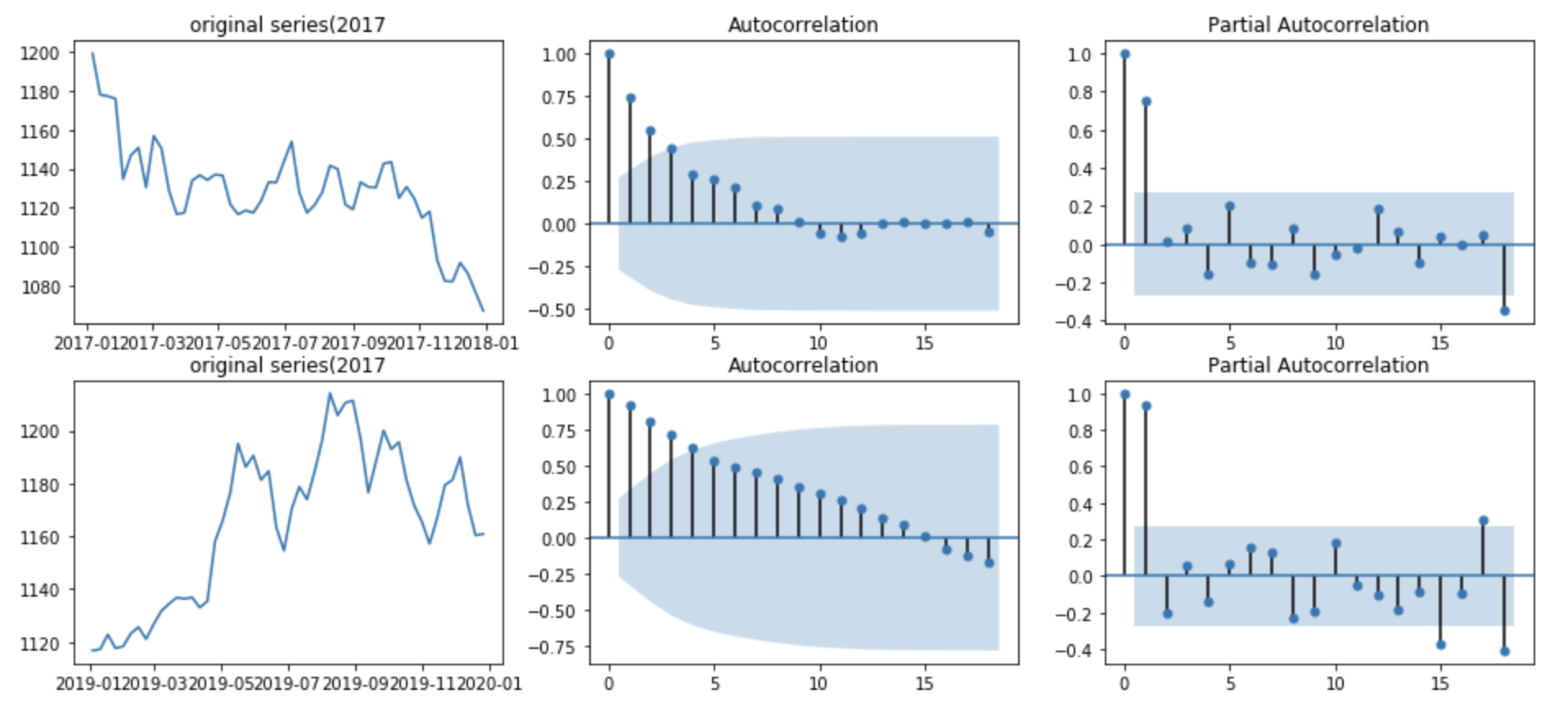
Auto Correlation Funtion 과 Partial Auto Correlation Function을 통해서 어떻게 시계열 데이터에 인사이트를 뽑을 수 있을지 간단하게 알아보겠습니다.이전 포스팅에서 사용했던 환율데이터를 사용하겠습니다.먼저 해당데이터는 일자별로

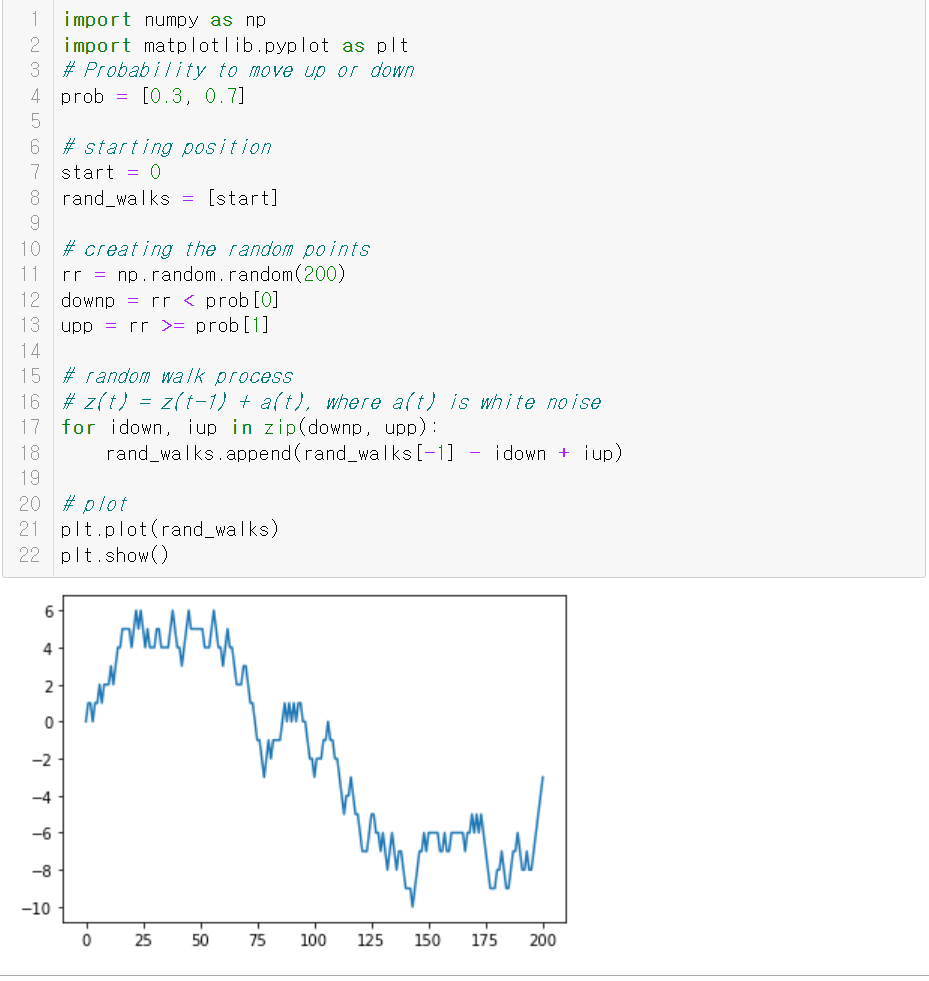
ARIMA모델의 잘 알려진 몇가지 모델에 대해 정리해 보았다.ARIMA(0,0,0), 백색잡음 모델 백색잡음 모델은 자기상관이 없는 시계열을 뜻한다. 즉, 강한 정상성을 가지고 있는 시계열 데이터라고 할 수 있다.또한 상관관계를 확인해보기 위해 자기상관함수도표(ACF

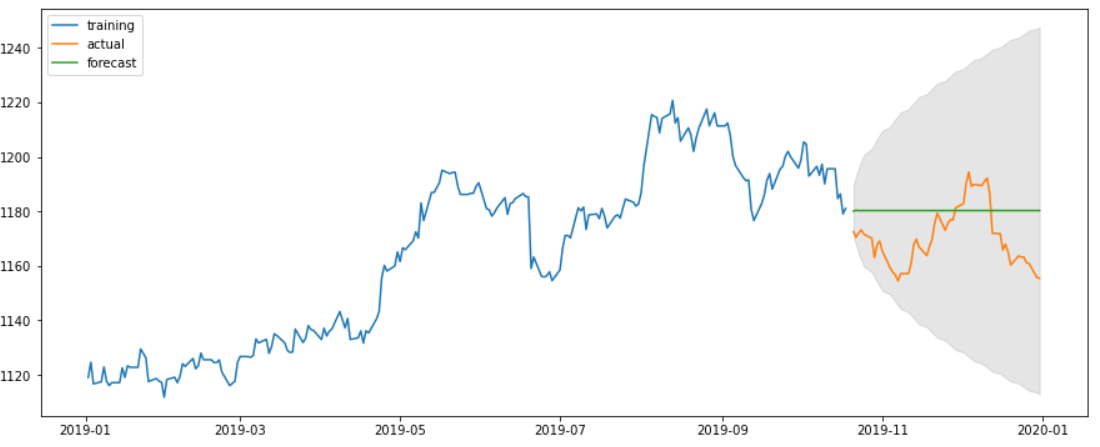
AR(p) 모델 현재 차수(Yt)의 결과는 이전차수(Yt-1)의 결과에 영향을 받는모델이다. 즉, 자신의 데이터가 이후 자신의 미래 관측값에 영향을 준다는 것을 기반으로 나온 모델이다. 외부 충격이 길게 반영되는 Long Memory 모델이다. MA(q) 모델 이번