ARIMA모델 종류

ARIMA모델의 잘 알려진 몇가지 모델에 대해 정리해 보았다.

1. ARIMA(0,0,0), 백색잡음 모델

• 백색잡음 모델은 자기상관이 없는 시계열을 뜻한다. 즉, 강한 정상성을 가지고 있는 시계열 데이터라고 할 수 있다.

• 또한 상관관계를 확인해보기 위해 자기상관함수도표(ACF plot)를 통해 확인해볼 수 있다.

• 시계열 데이터 통계 분석에서 백색잡음과정(white noise process)는 평균이0, 분산이 유한한 상수(sigma^2)인 확률분포로 부터 서로 상관되지 않게 무작위로 샘플을 추출한 신호를 말한다.

2. ARIMA(0,1,0), 확률보행 모델

• 확률보행(Randomg WalK)과정은 백색잡음과 달리 '비정상성'을 가지고 있는 데이터이다. 따라서 ARIMA모델에 적용시키기 위해서는 정상화 시켜야한다.

• 확률보행의 경우 임의의 방향으로 향하는 연속적인 걸음을 나타내는 의미로, 예측 불가능한 변동이 발생하는 것을 뜻한다. 예를들어 위로갈 확률이 0.3, 아래로 갈 확률이 0.7일 경우 아래와 같이 오르락 내리락 할것이다.
  

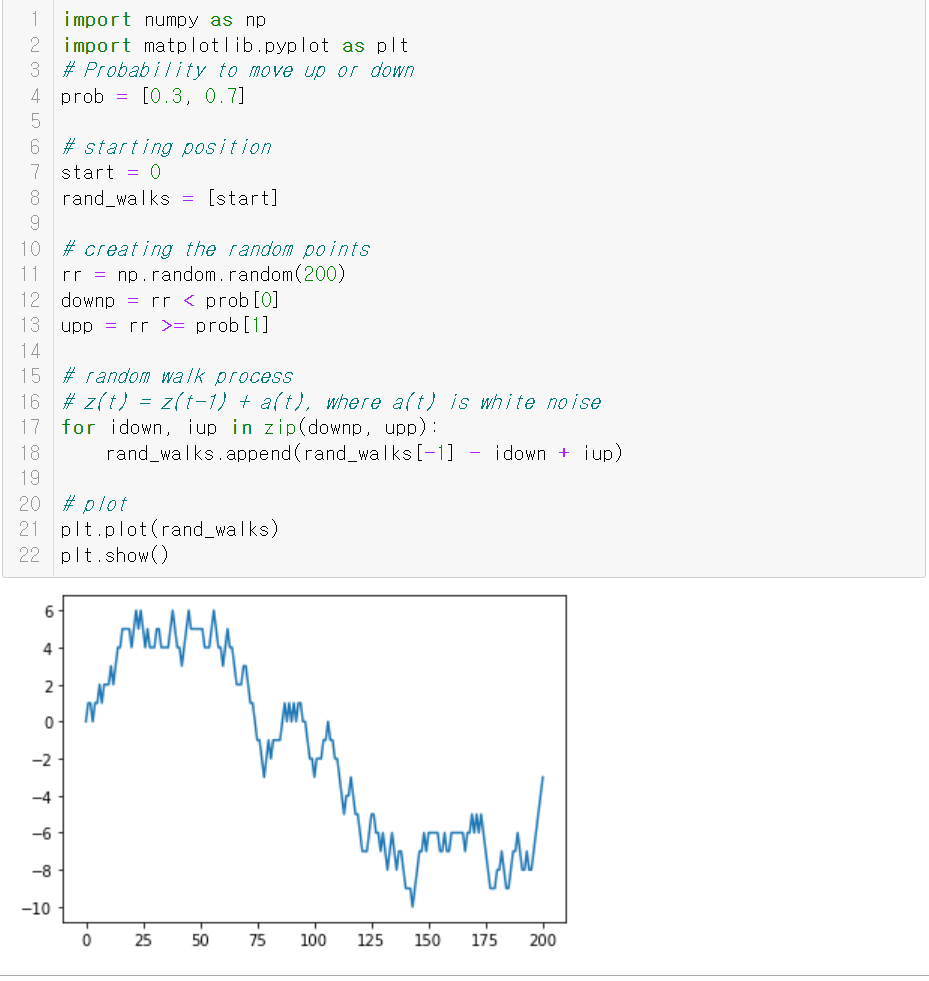
3. ARIMA(p,0,0), 자귀회귀 모델

• 자귀회귀모델(AutoRegression)은 자신의 과거시점을 통해 예측하는 모델을 말한다.
  (자세한 설명은 오른쪽 링크에 작성해 두었다.
  https://velog.io/@ljs7463/%EC%8B%9C%EA%B3%84%EC%97%B4-%EB%8D%B0%EC%9D%B4%ED%84%B0-%EC%A0%95%EC%83%81%EC%84%B1%EC%95%88%EC%A0%95%EC%84%B1-stationary-AR-MR-ACF-PACF )

4. ARIMA(0,0,q), 이동평균 모델

• 이동평균(Moving Average)모델은 이전시점과의 오차항을 통해 예측하는 모델이며 마찬가지로
  아래 링크에 자세하게 작성해 두었다.
  https://velog.io/@ljs7463/%EC%8B%9C%EA%B3%84%EC%97%B4-%EB%8D%B0%EC%9D%B4%ED%84%B0-%EC%A0%95%EC%83%81%EC%84%B1%EC%95%88%EC%A0%95%EC%84%B1-stationary-AR-MR-ACF-PACF